Lentille convergente : aberrations géométriques
1. Introduction
La lentille convergente constitue un système centré élémentaire permettant de mettre en évidence les différentes formes d'aberrations géométriques. Par ailleurs, l'objectif d'une lunette astronomique est constitué, dans sa forme la plus simple, d'une lentille convergente.
L'étude des aberrations sera faite avec le module Python décrit dans Dioptres centrés : optique géométrique.
On considère tout d'abord une lentille simple bi-convexe puis on verra comment diminuer notablement les aberrations sphérique et chromatique en remplaçant la lentille par un doublet.
Soit une lentille bi-convexe dont les deux faces ont le même rayon de courbure, égal à 1 par convention. La focale est d'environ 1. Le diamètre est choisi égal à 0.1, ce qui correspond à un rapport f/D de 10. Voici tout d'abord le chargement des modules et la définition de la lentille :
from IndiceVerre import *
from Dioptres import *
from pylab import *
cat = CatalogueVerre()
n1 = Vide()
n2 = cat.verre['N-BK7']
e = 0.01
c = 1.0
r = 0.05
dioptre1 = Spherique(-e/2,c,n1,n2,r)
dioptre2 = Spherique(e/2,-c,n2,n1,r)
lentille = SystemeCentre()
lentille.ajouter(dioptre1)
lentille.ajouter(dioptre2)
figure()
[x1,z1] = dioptre1.profil(20)
plot(z1,x1,color='b')
[x2,z2] = dioptre2.profil(20)
plot(z2,x2,color='b')
xlabel('z')
ylabel('x')
axis([-0.1,0.1,-0.05,0.05])
grid(True)
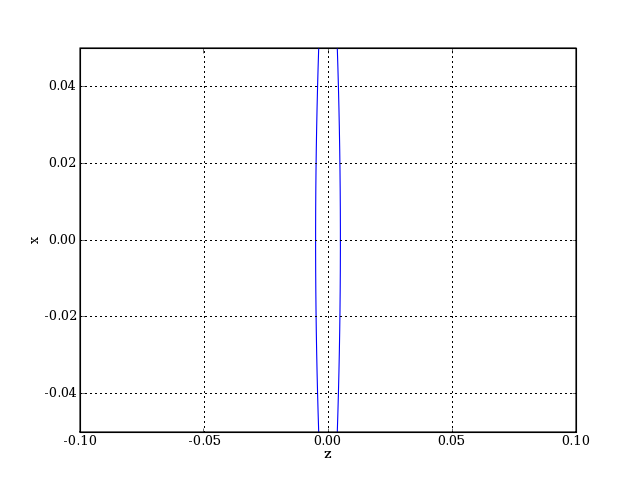plotA.pdf
On calcule les foyers et plans principaux pour la raie d:
raie = 'd'
lentille.matriceTransfert(raie)
[Fo,Fi,Ho,Hi] = lentille.foyers(raie)
print([Fo.z,Fi.z,Ho.z,Hi.z]) --> [-0.97084124065649779, 0.97084124065649779, -0.0016979611891565867, 0.0016979611891565867]
2. Aberration sphérique
On considère un faisceau de rayons méridiens parallèles à l'axe de la lentille. En pratique, un tel faisceau est obtenu avec une source ponctuelle située à l'infini. Pour les rayons proches de l'axe, l'image de cette source est le foyer image.
f = FaisceauParalleleMeridien(10,0.0,-1.0,r)
lentille.refractionFaisceau(f,raie)
figure()
plot(z1,x1,color='b')
plot(z2,x2,color='b')
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1)
plot(XYZ[2],XYZ[0],color='y')
xlabel('z')
ylabel('x')
axis([-1,2,-0.05,0.05])
grid(True)
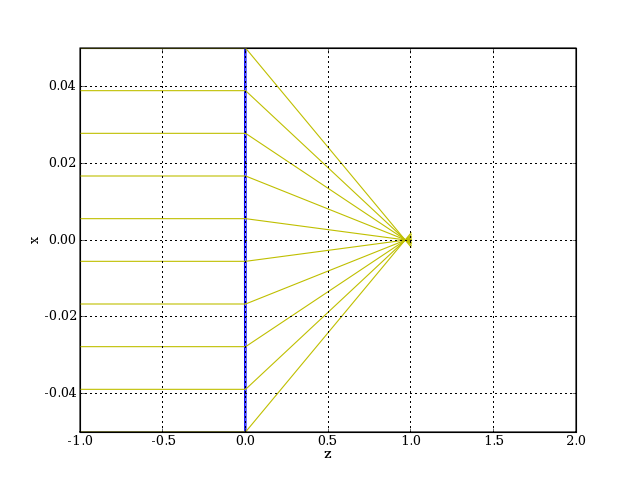plotB.pdf
Voyons en détail la zone de convergence de ces rayons :
axis([0.96,0.98,-0.001,0.001])
plotC.pdf
On constate que les rayons qui traversent la lentille près de son bord convergent sur l'axe un peu à gauche des rayons paraxiaux. Bien que le foyer soit à z=.97, la position du plan image donnant l'image la plus petite est à environ z=0.9675 (cercle de moindre confusion). Pour une lunette astronomique de focale 1 m, le rayon du cercle image est alors d'environ 0.1 mm, ce qui est considérable. Il faut comparer cette taille à la largeur de la tache de diffraction de l'ouverture de la lentille (10 cm) dans le plan focal, soit 14 micromètres pour la raie d.
L'aberration sphérique longitudinale (ASL) est par définition la distance entre le foyer image et le point de convergence des rayons méridiens traversant la lentille près de son bord. La fonction suivante calcule l'ASL d'un système optique.
def ASL(systeme,raie,r):
systeme.matriceTransfert(raie)
[Fo,Fi,Ho,Hi] = systeme.foyers(raie)
R = Rayon([r,0,-100.0],[0,0,1.0])
Rc = RayonComplet()
Rc.ajouter(R)
systeme.refraction(Rc,raie)
R2 = Rc.getRayon()
t = -R2.P[0]/R2.U[0]
z = R2.P[2]+R2.U[2]*t
return Fi.z - z
Par exemple pour la lentille précédente :
asl = ASL(lentille,raie,r)
print(asl) --> 0.0041649302283
Pour réduire l'aberration sphérique, il faut réduire la courbure de la face du côté du foyer. Pour cela, il faut faire varier aussi la courbure de l'autre face, de manière à maintenir la distance focale constante en utilisant la relation suivante, valable pour une lentille mince :
La fonction suivante calcule l'ASL d'une lentille convergente (objet à l'infini) de focale précisée pour une courbure donnée de la face de sortie :
def AslLentille(raie,r,nv,f,c2):
n1 = Vide()
c1 = c2+1.0/(f*(nv.indice(raie)-1))
e = 0.01
dioptre1 = Spherique(-e/2,c1,n1,nv,r)
dioptre2 = Spherique(e/2,c2,nv,n1,r)
lentille = SystemeCentre()
lentille.ajouter(dioptre1)
lentille.ajouter(dioptre2)
return ASL(lentille,raie,r)
On trace l'ASL en fonction de la courbure de la face arrière :
c2List = []
asl = []
N = 30
for k in range(N):
c2 = -1.0*k/N
c2List.append(c2)
asl.append(AslLentille(raie,r,n2,1.0,c2))
figure()
plot(c2List,asl,color='b')
xlabel('c2')
ylabel('ASL')
grid(True)
axis([-1.0,0.0,0,0.005])
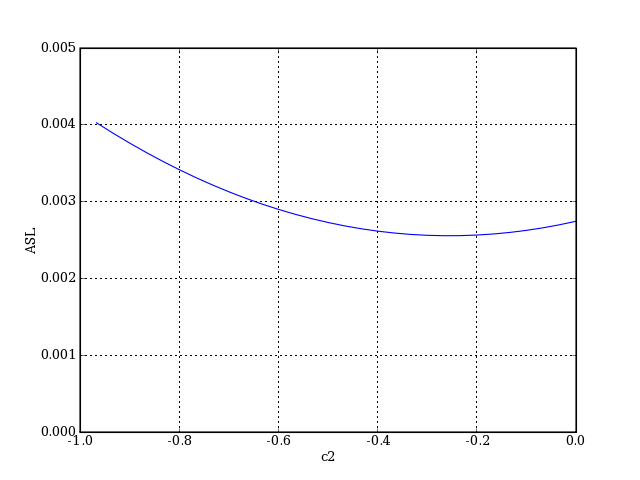plotD.pdf
L'aberration sphérique longitudinale est minimale pour une courbure de -0.3. Voyons le tracé des rayons dans ce cas :
c2 = -0.3
f = 1.0
c1 = c2+1.0/(f*(n2.indice(raie)-1))
dioptre1.c = c1
dioptre2.c = c2
f = FaisceauParalleleMeridien(10,0.0,-1.0,r)
lentille.refractionFaisceau(f,raie)
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1)
plot(XYZ[2],XYZ[0],color='y')
xlabel('z')
ylabel('x')
axis([0.98,1.01,-0.001,0.001])
grid(True)
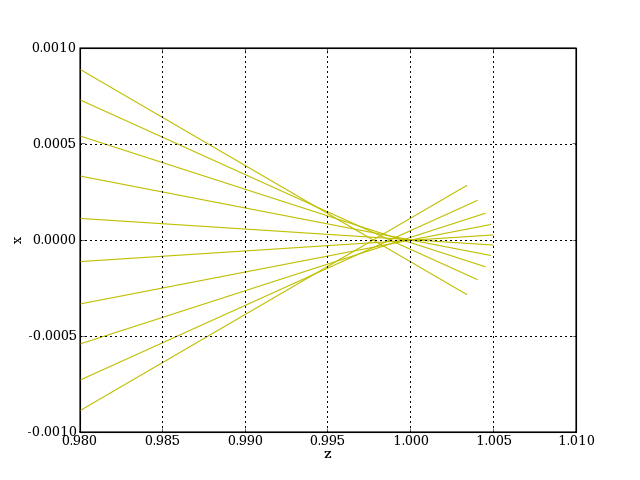plotE.pdf
asl = AslLentille(raie,r,n2,1.0,c2)
print(asl) --> 0.0025609833625
Le cercle de moindre de confusion a un rayon inférieur à 0.1 mm, mais qui reste grand par rapport à la taille de la tache de diffraction (0.014 mm). Pour réduire plus l'aberration sphérique (sans changer le rapport f/D), il faut associer plusieurs lentilles. On verra plus loin le cas du doublet.
3. Aberration chromatique
La fonction suivante calcule l'aberration chromatique longitudinale, c'est-à-dire le décalage des foyers pour deux raies différentes. Elle calcule aussi la distance focale image pour la raie d (jaune).
def ACL(systeme,raie1,raie2):
systeme.matriceTransfert(raie1)
[Fo,Fi,Ho,Hi] = systeme.foyers(raie)
z1 = Fi.z
systeme.matriceTransfert(raie2)
[Fo,Fi,Ho,Hi] = systeme.foyers(raie)
acl = Fi.z - z1
systeme.matriceTransfert('d')
[Fo,Fi,Ho,Hi] = systeme.foyers('d')
fD = Fi.z - Hi.z
return [acl,fD]
Pour la lentille précédente, l'aberration longitudinale pour les raies F et C de Fraunhofer :
[acl,fD] = ACL(lentille,'F','C')
print([acl,fD]) --> [0.015467493850904068, 1.0008644240519311]
L'aberration chromatique est environ 6 fois plus forte que l'aberration sphérique. Pour la réduire, on réalise un doublet en plaçant une lentille divergente à l'arrière de la lentille convergente, faite d'un verre plus dispersif (verre flint dense). Voyons par exemple un doublet de Fraunhofer, formé d'une lentille bi-convexe, dont les rayons de courbure seront ajustés, et d'une lentille concave-plan accolée à la première.
La fonction suivante calcule l'ACL pour un doublet spécifié en argument, pour les raies F et C de Fraunhofer.
def AclDoublet(c1,c2,n2,n3,e1,e2,r):
n1 = Vide()
dioptre1 = Spherique(0,c1,n1,n2,r)
dioptre2 = Spherique(e1,c2,n2,n3,r)
dioptre3 = Spherique(e1+e2,0,n3,n1,r)
systeme = SystemeCentre()
systeme.ajouter(dioptre1)
systeme.ajouter(dioptre2)
systeme.ajouter(dioptre3)
[acl,fD] = ACL(systeme,'F','C')
return [acl,fD]
La lentille convergente est en verre crown alors que la lentille divergente est en verre flint, dont l'indice et le pouvoir dispersif sont plus élevés :
n2 = cat.verre['N-BK7']
n3 = cat.verre['F5']
Tracé de l'ACL pour différentes valeurs de la courbure c2 :
e1 = 0.01
e2 = 0.007
r = 0.05
c1 = 2.4
y = []
c2List = []
N = 10
for k in range(N):
c2 = -2.0-1.0/N*k
c2List.append(c2)
[acl,fD] = AclDoublet(c1,c2,n2,n3,e1,e2,r)
y.append(acl)
figure()
plot(c2List,y,color='b')
xlabel('c2')
ylabel('ACL')
grid(True)
axis([-2.6,-2.4,-0.001,0.001])
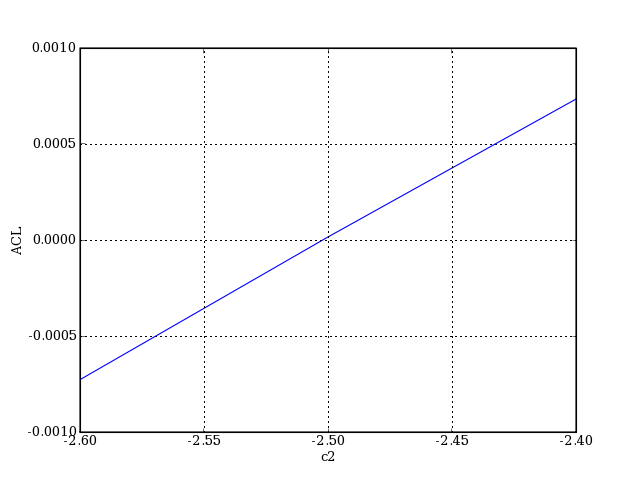plotF.pdf
L'ACL s'annule pour c2 = -2.50. On choisit donc cette valeur pour définir le doublet. Dans ce cas, les foyers (au sens de l'optique paraxial) des raies C et F coïncident; le doublet est dit achromatique. Le polissage d'une pièce de verre étant limité en précision, on retiendra une valeur approchée à 1% près.
c2 = -2.50
dioptre1 = Spherique(0,c1,n1,n2,r)
dioptre2 = Spherique(e1,c2,n2,n3,r)
dioptre3 = Spherique(e1+e2,0,n3,n1,r)
doublet = SystemeCentre()
doublet.ajouter(dioptre1)
doublet.ajouter(dioptre2)
doublet.ajouter(dioptre3)
figure()
[x1,z1] = dioptre1.profil(20)
plot(z1,x1,color='b')
[x2,z2] = dioptre2.profil(20)
plot(z2,x2,color='b')
[x3,z3] = dioptre3.profil(20)
plot(z3,x3,color='b')
xlabel('z')
ylabel('x')
axis([-0.1,0.1,-0.05,0.05])
grid(True)
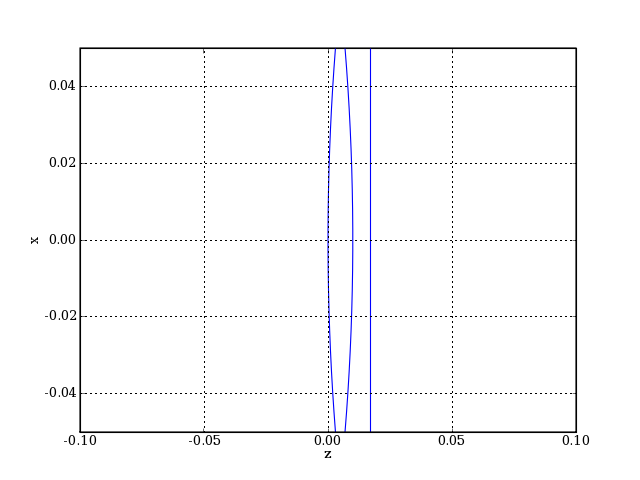plotG.pdf
Aberrations et focale pour ce doublet :
[acl,fD] = ACL(doublet,'F','C')
asl = ASL(doublet,'d',r)
print([acl,asl,fD]) --> [1.5788096151880815e-05, 0.000250188006819, 0.97509530917898124]
Comme prévu, l'ACL pour les raies F et C est très faible, mais pas nulle car la courbure utilisée est une valeur approchée de la courbure qui annulerait l'ACL. On constate aussi une réduction de l'aberration sphérique d'un facteur 10 par rapport à la lentille bi-convexe. Pour réduire encore cette dernière, il faut modifier la courbure de le face arrière de la lentille divergente. C'est un calcul beaucoup plus complexe puisqu'il faut optimiser à la fois l'ACL et l'ASL en modifiant plusieurs courbures.
On calcule aussi l'ACL entre les raies F et d :
[acl,fD] = ACL(doublet,'F','d')
print(acl) --> -0.00049420206987560444
Il y a donc un chromatisme secondaire de l'ordre de 0.5 mm (pour une focale de 1 m).
Voyons le tracé des rayons méridiens pour les raies F, C et d :
figure()
f = FaisceauParalleleMeridien(10,0.0,-1.0,r)
doublet.refractionFaisceau(f,'C')
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(2)
plot(XYZ[2],XYZ[0],color='r')
f = FaisceauParalleleMeridien(10,0.0,-1.0,r)
doublet.refractionFaisceau(f,'F')
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(2)
plot(XYZ[2],XYZ[0],color='b')
f = FaisceauParalleleMeridien(10,0.0,-1.0,r)
doublet.refractionFaisceau(f,'d')
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(2)
plot(XYZ[2],XYZ[0],color='y')
xlabel('z')
ylabel('x')
axis([0.978,0.982,-0.0001,0.0001])
grid(True)
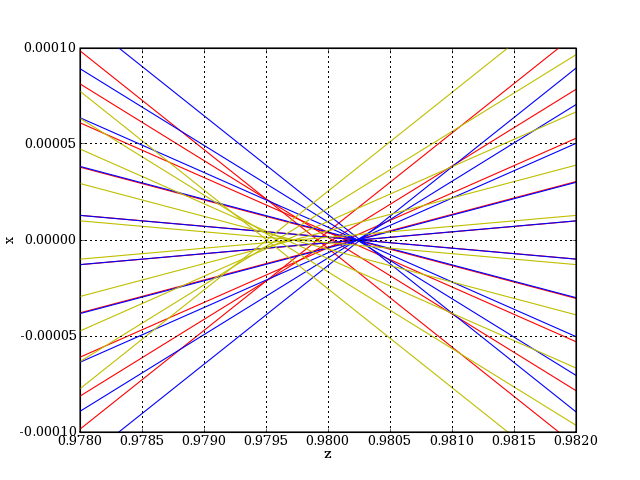plotI.pdf
Bien qu'il y ait coïncidence des foyers rouge et bleu pour les rayons paraxiaux, les rayons inclinés convergent en des points notablement décalés. Cela montre que l'aberration sphérique a un effet sur l'aberration chromatique. En raisonnant sur les cercles de moindre confusion, on voit sur cette figure que le décalage entre les images bleu et jaune atteint environ 0.75 mm.
Pour la raie d (jaune), le cercle de moindre confusion a environ 10 micromètre de diamètre, soit une valeur inférieur au diamètre de la tache de diffraction d'Airy (14 micromètres). La limite de la diffraction est donc atteinte sur l'axe en lumière monochromatique. En revanche, l'utilisation d'une lumière blanche conduit à un étalement transversal de la lumière, avec des irrisations, bien au delà de la tache de diffraction.
4. Aberration de coma
L'aberration de coma se manifeste pour un point objet hors de l'axe. Nous allons mettre en évidence cette aberration avec le doublet précédent, bien qu'il ne soit pas complètement corrigé des aberrations sphérique et chromatique. Les aberrations sont souvent considérées séparément les unes des autres, mais en pratique elles sont présentes simultanément.
Les rayons sont répartis sur un cylindre de révolution. Voici un exemple de tracé des rayons vu en projection :
alpha = 0.05
f = FaisceauParalleleCylindre(30,alpha,-0.1,0.02)
doublet.refractionFaisceau(f,'d')
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1.5)
plot(XYZ[2],XYZ[0],color='y')
xlabel('z')
ylabel('x')
plot(z1,x1,color='b')
plot(z2,x2,color='b')
plot(z3,x3,color='b')
grid(True)
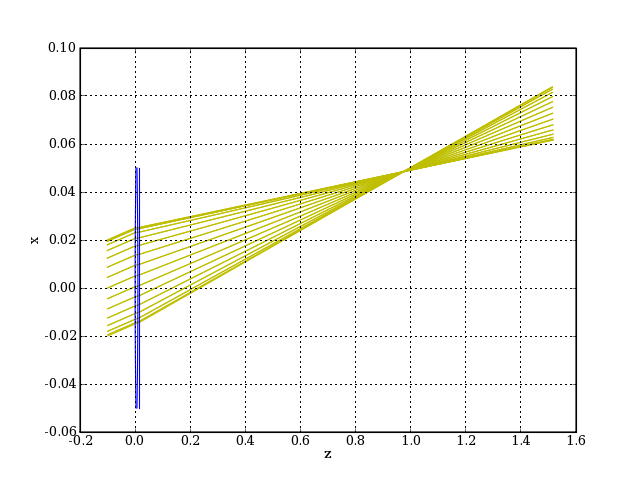plotJ.pdf
On remarquera que seuls deux rayons de ce faisceau sont méridiens, compris dans le plan Oxz : le rayon du haut et celui du bas sur la figure. On trace l'intersection des rayons avec le plan image correspondant au cercle de moindre confusion de la raie d. Pour un faisceau cylindrique de rayon donné, on obtient dans le plan image une courbe fermée.
zi = 0.9795
planImage = PlanImage(zi,0.1)
doublet.ajouter(planImage)
def pointsImage(systeme,alpha,r,raie,color):
f = FaisceauParalleleCylindre(30,alpha,-0.1,r)
systeme.refractionFaisceau(f,raie)
x = []
y = []
for Rc in f.listeRayons:
R = Rc.getRayon()
x.append(R.P[0])
y.append(R.P[1])
plot(x,y,color=color)
figure(figsize=(7,7))
alpha = 0.005
rList = [0.001,0.005,0.01,0.015,0.02,0.025,0.03,0.035]
for r1 in rList:
pointsImage(doublet,alpha,r1,'d','y')
xlabel('x')
ylabel('y')
grid(True)
axis([0.004860,0.004880,-0.00001,0.00001])
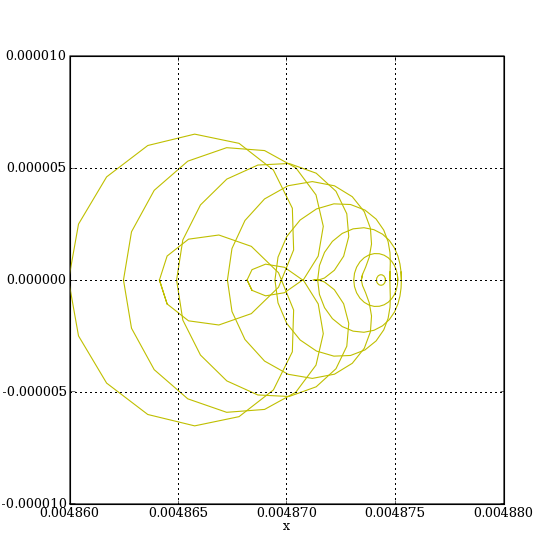plotK.pdf
La coma se traduit par un alongement de l'image dans la direction x, lui donnant l'aspect d'une comète.
Pour comparaison, voici la même figure pour un angle nul :
figure(figsize=(7,7))
alpha = 0
for r1 in rList:
pointsImage(doublet,alpha,r1,'d','y')
xlabel('x')
ylabel('y')
grid(True)
axis([-0.00001,0.00001,-0.00001,0.00001])
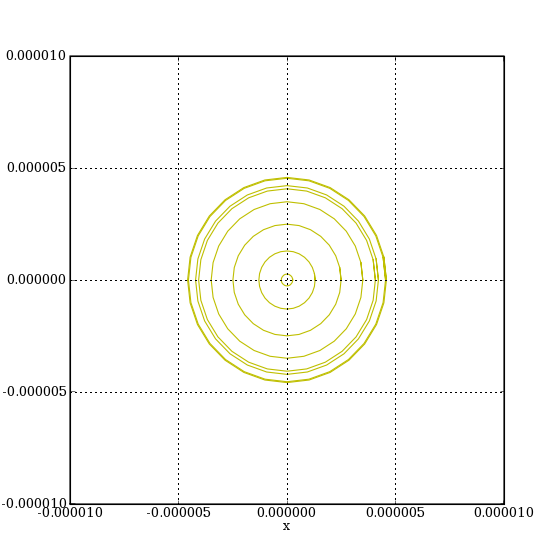plotL.pdf
Dans ce cas, seule l'aberration sphérique se manifeste.
5. Astigmatisme et courbure de champ
Comme la coma, l'astigmatisme se manifeste pour un objet ponctuel hors de l'axe de la lentille. Si l'objet est à l'infini, l'astigmatisme est visible pour un faisceau de rayons parallèles très fin. Dans ce cas, les aberrations sphérique et de coma sont très faibles. Bien entendu, pour un faisceau limité par le diamètre de la lentille, les trois aberrations se mélangent.
Parmi les rayons de ce faisceau, certains sont contenus dans le plan méridien, c'est-à-dire le plan défini par le rayon central (passant par le centre de la lentille) et l'axe de la lentille. Ce plan est appelé plan tangentiel. On considère aussi les rayons contenus dans un plan perpendiculaire au précédent, appelé plan sagittal. Le plan tangentiel est ici le plan Oxz.
Voici tout d'abord le tracé des rayons en projection sur le plan Oxz. Seule la zone de convergence est montrée.
alpha = 0.02
f = FaisceauParallele(20,alpha,-0.1,0.001)
doublet.refractionFaisceau(f,'d')
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1)
plot(XYZ[2],XYZ[0],color='y')
xlabel('z')
ylabel('x')
grid(True)
axis([0.978,0.98,0.01948,0.0195])
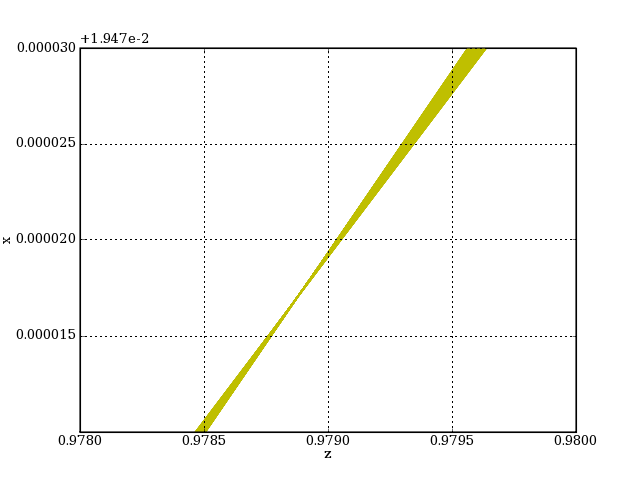plotM.pdf
Le même faisceau vu en projection sur le plan Oyz :
figure()
for Rc in f.listeRayons:
XYZ = Rc.getXYZ(1)
plot(XYZ[2],XYZ[1],color='y')
xlabel('z')
ylabel('x')
grid(True)
axis([0.978,0.98,-0.00001,0.00001])
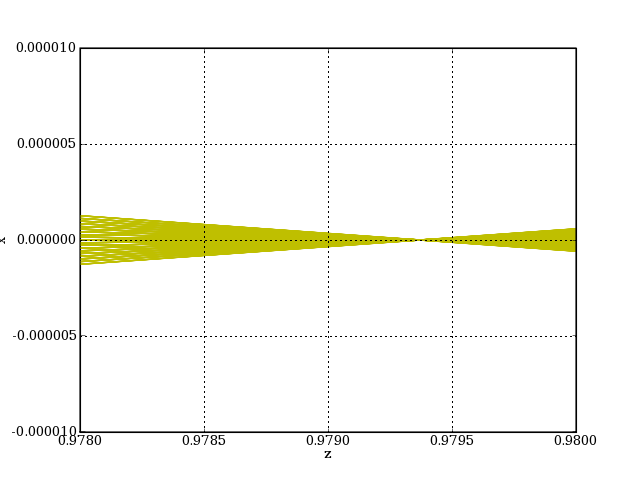plotN.pdf
L'astigmatisme se manifeste ici par un décalage du point de convergence des rayons d'environ 0.0005. Les rayons du plan tangentiel (rayons méridiens) convergent vers un foyer légèrement plus proche de la lentille que le foyer des rayons du plan sagittal. Pour le faisceau complet, le cercle de moindre confusion est à mi-chemin entre ces deux foyers.
D'autre part, le cercle de moindre confusion sur l'axe de la lentille est à z=0.9795, soit à environ 0.0005 à droite du cercle de moindre de confusion obtenu ici, c'est-à-dire pour une image se formant à 0.02 de l'axe. Ce décalage est la manifestation de la courbure de champ : les cercles de moindre confusion se répartissent sur une sphère et non sur un plan. Pour la lunette de focale 1 m, l'image formée à 2 cm de l'axe est décalée de 0.5 mm par rapport à l'image de l'axe.
6. Conclusion
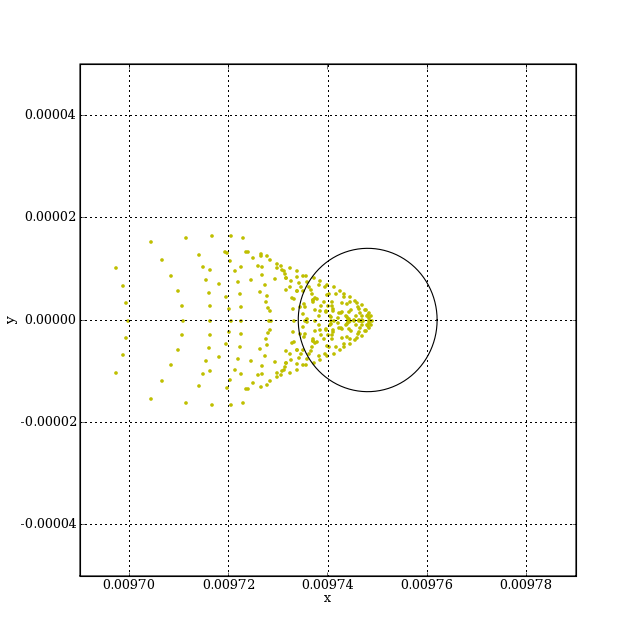
Pour conclure, voyons l'aspect de l'image d'une étoile se formant à 1 cm de l'axe, dans le plan de moindre confusion obtenu sur l'axe. Ce cas correspond à une mise au point de la lunette astronomique effectuée sur l'axe. L'étoile est à environ 0.6 ° de l'axe.
planImage.z = 0.9795
alpha = 0.01
f = FaisceauParallele(20,alpha,-0.1,0.05)
doublet.refractionFaisceau(f,'d')
figure(figsize=(8,8))
for Rc in f.listeRayons:
P = Rc.getRayon().P
plot([P[0]],[P[1]],color='y',marker='.')
rAiry = 0.000014
angles = linspace(0,2*pi,100)
xi = 0.009748
plot(xi+rAiry*cos(angles),rAiry*sin(angles),color='k')
xlabel('x')
ylabel('y')
grid(True)
axis([0.00969,0.00969+0.0001,-0.00005,0.00005])
plotO.pdf
Pour comparaison, la tache de diffraction est représentée par un cercle. L'aberration de coma est nettement visible. En lumière blanche, l'effet de l'aberration chromatique est prépondérant. Pour obtenir une représentation plus réaliste des images, il faut bien sûr tenir compte de la diffraction.
