Transfert d'énergie par couplage inductif : expérience
1. Introduction
Ce document présente la conception et la réalisation d'un système de transfert d'énergie par couplage inductif.
Les bobines plates utilisées pour le couplage inductif sont deux bobines identiques fabriquées par Wurth Electronik, de taille 40x40x1.2 mm, d'inductance 8 μH et acceptant un courant maximal de 5 A.

Comme on le voit sur la photo ci-dessus, la bobine est collée sur une plaque en ferrite magnétique. Ce type de bobine est vendu pour réaliser des chargeurs sans fil.
Le problème général du transfert d'énergie par induction est présenté dans Transfert d'énergie par couplage inductif.
Les mesures sont réalisées avec l'Analog Discovery 2 et avec le logiciel Waveforms.
2. Circuit de couplage et simulation
L'objectif est de transférer une puissance entre une alimentation très basse tension de laboratoire (d'une puissance maximale de quelques dizaines de watts) et une charge résistive de quelques ohms. Pour la modélisation et les premiers essais, nous optons pour une résistance de charge Rc=5 Ω. Une tension de 10 V appliquée à cette charge correspond à une puissance reçue de 20 W. La fréquence de travail (fréquence de découpage par le pont de transistors) devra se situer entre 10 kHz et 100 kHz.
L'étude des bobines de couplage est exposée dans Bobines avec noyau. Leur inductance est L1=L2=8,5 μH. Leur résistance à 90 kHz est r1=r2=0,18 Ω.
La bobine du circuit primaire (bobine 1) est mise en parallèle avec un condensateur de capacité C1=600 nF afin d'obtenir une maille résonante. Celle-ci est reliée à la source de tension E par une bobine d'inductance L0. Il s'agit d'une bobine réalisée par enroulement d'un fil de cuivre de diamètre 9 mm sur un noyau en ferrite cylindrique. La valeur de L0 peut être modifiée en faisant coulisser le noyau, entre 2 microhenrys (noyau complètement sorti) et 20 microhenrys (noyau complètement inséré). Cette bobine est étudiée dans Bobines avec noyau. Lorsque L0=10 μH, sa résistance série à 90 kHz est r0=0,22 Ω.
Il faut remarquer que les valeurs de résistances internes des bobines à 90 kHz sont beaucoup plus grandes que les résistances DC. On choisit de prendre pour le modèle les résistances à 90 kHz car la résonance des tensions U1 et U2 a lieu pour une fréquence voisine de 90 kHz et on se servira de la courbe de résonance pour ajuster la valeur de k par comparaison avec les courbes expérimentales. La résistance rc1 est la résistance série modélisant les pertes dans le condensateur. Ce condensateur est réalisé avec des condensateurs MKP de tension maximale 300 V : deux condensateurs de 1 μF en série, en parallèle avec un condensateur de 100 nF. Nous ne connaissons pas précisément la résistance série à 100 kHz mais une comparaison avec les résultats expérimentaux (montrés plus loin) montre que rc1=0,1 Ω est l'ordre de grandeur de cette résistance. L'ajustement du modèle sur la courbe expérimentale permettra de préciser la valeur de rC1.
Figure pleine pageLes équations permettant de calculer les courants en régime sinusoïdal sont :
Pour chaque fréquence, on résout ce système numériquement avec la fonction numpy.linalg.solve. La fonction suivante renvoie les intensités des trois courants, les tensions U1 et U2, P0, la puissance délivrée par la source et P2 la puissance reçue par la charge. k est le coefficient de couplage entre les deux bobines, compris entre 0 et 1.
import numpy as np
from matplotlib.pyplot import *
from numpy.linalg import solve
def couplage(f,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc):
M = k*np.sqrt(L1*L2)
w = 2*np.pi*f
N = len(f)
I0 = np.zeros(N,dtype=complex)
I1 = np.zeros(N,dtype=complex)
I2 = np.zeros(N,dtype=complex)
for i in range(N):
A = np.zeros((3,3),dtype=np.complex64)
A[0,0] = r0+1j*L0*w[i]+1/(1j*C1*w[i])+rc1
A[0,1] = -1/(1j*C1*w[i])-rc1
A[1,0] = r0+1j*L0*w[i]
A[1,1] = 1j*L1*w[i]+r1
A[1,2] = 1j*M*w[i]
A[2,1] = 1j*M*w[i]
A[2,2] = 1j*L2*w[i]+r2+Rc
B = np.array([1,1,0])
X = solve(A,B)
I0[i],I1[i],I2[i] = X[0],X[1],X[2]
P0 = 0.5*np.real(I0)
P2 = 0.5*Rc*np.absolute(I2)**2
U1 = (r1+1j*L1*2*np.pi*f)*I1+1j*M*2*np.pi*f*I2
P1 = 0.5*np.real(I1*np.conjugate(U1))
U2 = Rc*I2
return I0,I1,I2,U1,U2,P0,P1,P2
Voici une fonction qui réalise différents tracés :
def trace(f,I0,I1,I2,U1,U2,P0,P1,P2,Plog = True):
figure(figsize=(16,8))
subplot(221)
plot(f,np.absolute(I1),label='I1')
plot(f,np.absolute(I2),label='I2')
plot(f,np.absolute(I0),label='I0')
yscale('log')
grid()
legend(loc='upper right')
ylabel('I/E (A/V)',fontsize=16)
subplot(223)
plot(f,np.absolute(U1),label='U1')
plot(f,np.absolute(U2),label='U2')
grid()
xlabel('f (Hz)',fontsize=16)
legend(loc='upper right')
ylabel(r"U/E",fontsize=16)
subplot(224)
plot(f,P2/P0)
grid()
ylabel('P2/P0',fontsize=16)
ylim(0,1.1)
xlabel('f (Hz)',fontsize=16)
subplot(222)
plot(f,P0,label='P0')
plot(f,P1,label='P1')
plot(f,P2,label='P2')
if Plog : yscale('log')
else : ylim(0,max(P1.max(),P2.max())*2)
grid()
legend(loc='upper right')
ylabel(r"$P/E^2\ (\rm W/V^2)$",fontsize=16)
Voici une simulation avec un coefficient de couplage k=0,5 et une charge de résistance Rc=5 Ω.
L1 = L2 = 8.5e-6 r1 = r2 = 0.18 L0 = 10e-6 r0 = 0.22 k = 0.5 Rc = 5 C1 = 0.61e-6 rc1 = 0.02 f = np.linspace(10e3,150e3,2000) I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc) trace(f,I0,I1,I2,U1,U2,P0,P1,P2)
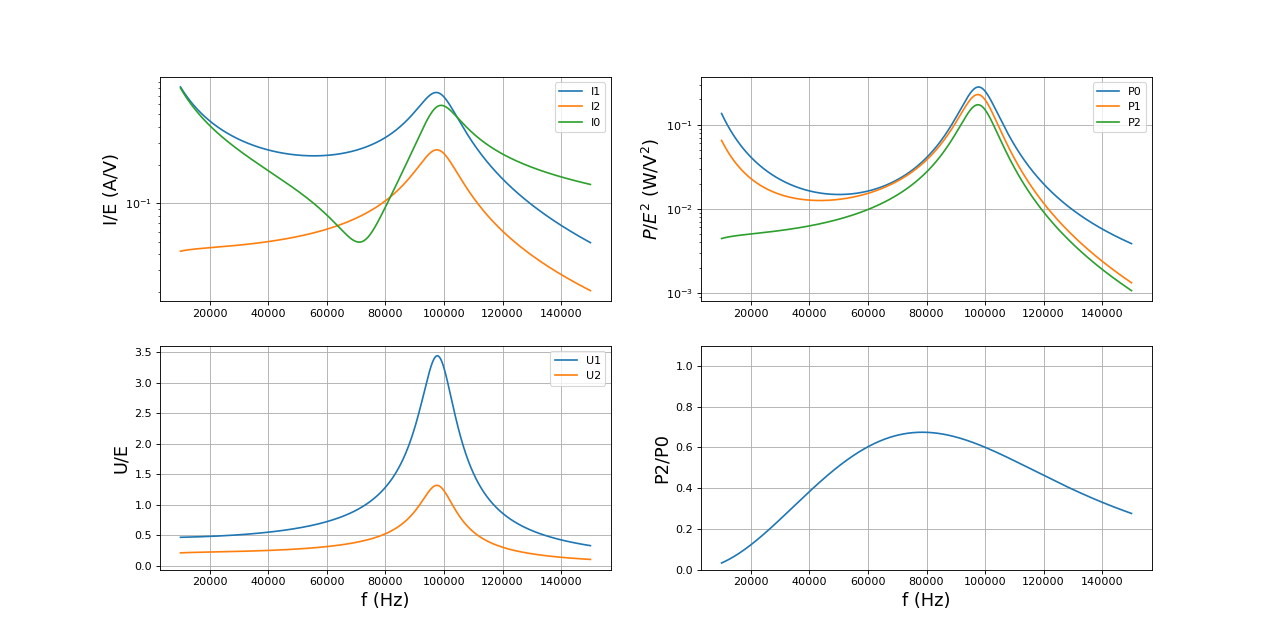 fig1.pdf
fig1.pdf
Le graphique en haut à gauche montre les trois amplitudes de courants. Le graphique en bas à gauche montre les tensions aux bornes des deux bobines de couplage. Le graphique en haut à droite montre les puissances moyennes, celle fournie par la source, celle reçue par la bobine primaire et celle reçue par la charge. Le graphique en bas à droite montre le rendement énergétique, c'est-à-dire le rapport de la puissance reçue par la charge par la puissance fournie par la source. La résonance de la maille L1C1 se traduit par un minimum de I0 à 70 kHz. L'auto-inductance L0 introduit une résonance à 95 kHz environ, qui maximise les puissances et les tensions.
Le rendement est maximal à 70 kHz. Cette fréquence est intéressante car le courant délivré par la source à cette fréquence est minimal, mais elle exige une tension plus grande (pour la même puissance délivrée) que la fréquence de résonance.
Voici le tracé des amplitudes des courants en fonction de E, à une fréquence de 90 kHz :
E = np.linspace(0,30)
f = 90e3
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(np.array([f]),L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure()
plot(E,E*np.absolute(I0[0]),label='I0')
plot(E,E*np.absolute(I1[0]),label='I1')
plot(E,E*np.absolute(I2[0]),label='I2')
grid()
ylim(0,10)
legend(loc='upper right')
xlabel('E (V)',fontsize=16)
ylabel('I (A)',fontsize=16)
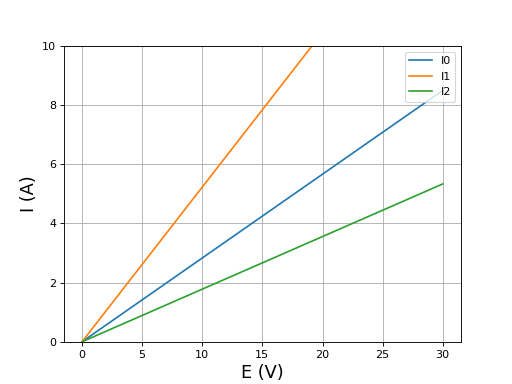 fig2.pdf
fig2.pdf
Une amplitude E=12 V permet de faire passer un courant de 2 A dans la charge et l'amplitude du courant délivré par la source est de 3 A. Ces valeurs sont compatibles avec l'utilisation d'une alimentation de laboratoire.
Voici les amplitudes des courants en fonction de E à une fréquence de 70 kHz :
E = np.linspace(0,30)
f = 70e3
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(np.array([f]),L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure()
plot(E,E*np.absolute(I0[0]),label='I0')
plot(E,E*np.absolute(I1[0]),label='I1')
plot(E,E*np.absolute(I2[0]),label='I2')
grid()
ylim(0,10)
legend(loc='upper right')
xlabel('E (V)',fontsize=16)
ylabel('I (A)',fontsize=16)
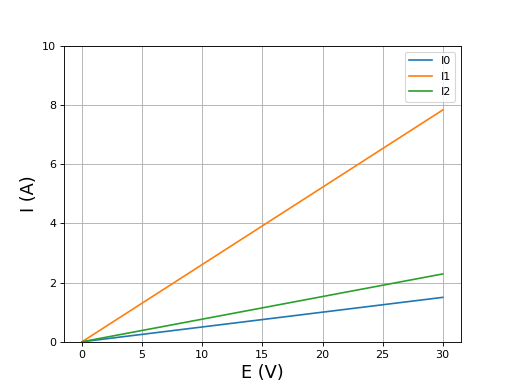 fig3.pdf
fig3.pdf
Pour faire passer un courant de 2 A dans la charge, il faut une tension E=25 V, ce qui est deux fois plus qu'à 90 kHz. En revanche, le courant demandé à la source n'est plus que de 2 A. Par ailleurs, le rendement est meilleur à cette fréquence.
Voici le comportement du système en l'absence de charge (résistance de charge grande) :
k = 0.5 Rc = 1e4 f = np.linspace(10e3,150e3,2000) I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc) trace(f,I0,I1,I2,U1,U2,P0,P1,P2) f_ref = f U1_ref = U1 # pour comparaison avec l'expérience
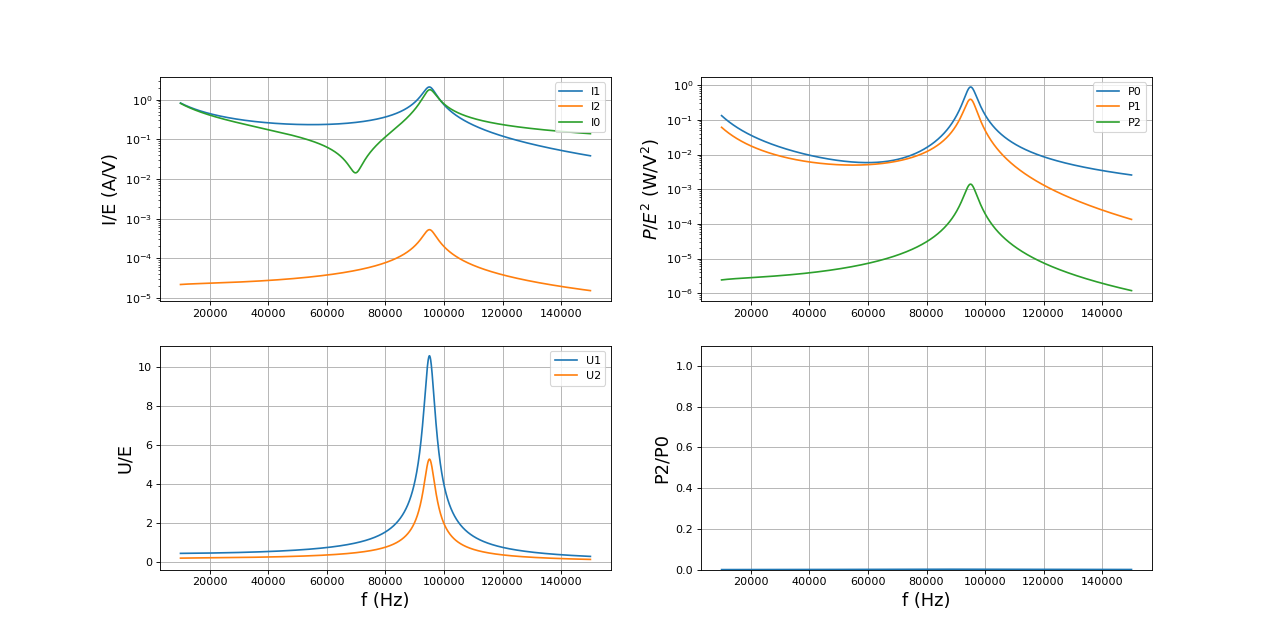 fig4.pdf
fig4.pdf
Le maximum des tensions à la résonance à 95 kHz est plus élevé mais à la fréquence de 70 kHz elles sont quasi inchangées. En l'absence de charge, l'énergie délivrée par la source est évidemment perdue et on aura donc intérêt à couper l'alimentation lorsque le circuit secondaire est éloigné donc il faudra trouver un moyen de détecter la proximité de celui-ci.
Voici les courbes avec la charge Rc=5 Ω mais avec un coefficient de couplage k=0,8 :
k = 0.8 Rc = 5 f = np.linspace(10e3,150e3,2000) I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc) trace(f,I0,I1,I2,U1,U2,P0,P1,P2)
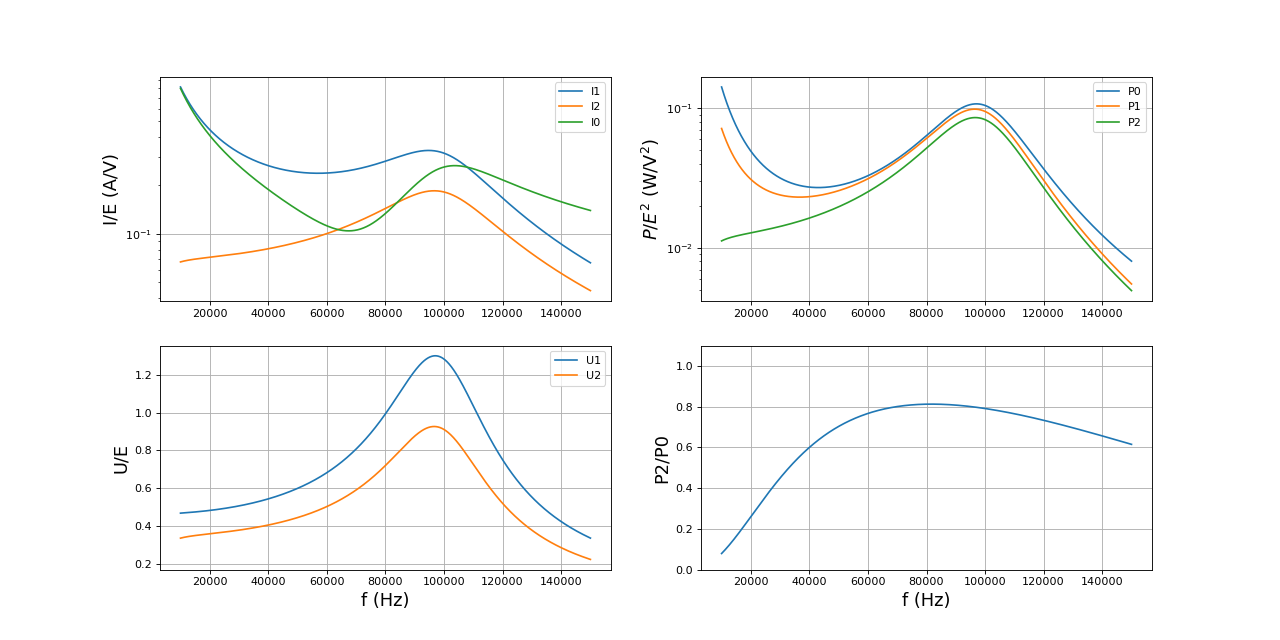 fig5.pdf
fig5.pdf
Ces courbes confirment l'intérêt de la fréquence 70 kHz. Voyons l'effet d'une réduction de la résistance de charge :
k = 0.8 Rc = 1 f = np.linspace(10e3,150e3,2000) I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc) trace(f,I0,I1,I2,U1,U2,P0,P1,P2)
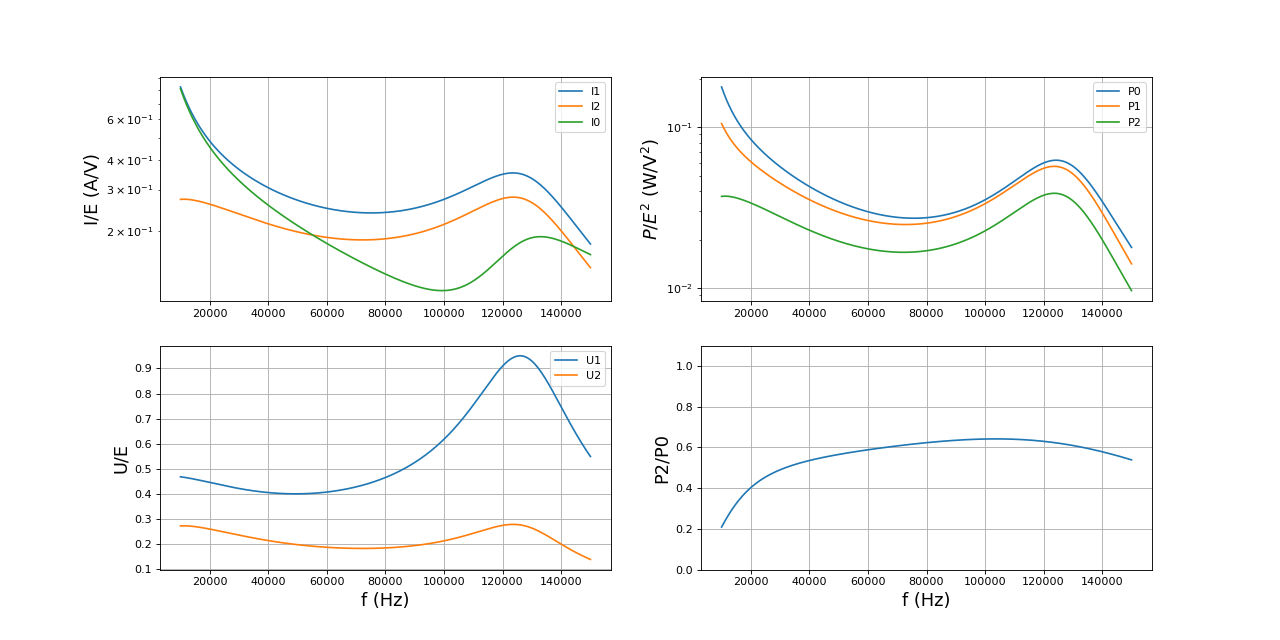 fig6.pdf
fig6.pdf
La fréquence de 70 kHz est toujours intéressante bien que I0 ne soit plus minimale à cette fréquence.
La figure suivante montre U2/E en fonction de la fréquence, pour Rc=5 Ω et différentes valeurs du coefficient de couplage :
Rc = 5
figure(figsize=(10,6))
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,0.9,r0,r1,r2,C1,rc1,Rc)
plot(f,np.absolute(U2),label='k=0,9')
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,0.5,r0,r1,r2,C1,rc1,Rc)
plot(f,np.absolute(U2),label='k=0,5')
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,0.2,r0,r1,r2,C1,rc1,Rc)
plot(f,np.absolute(U2),label='k=0,2')
grid()
xlabel("f (Hz)",fontsize=16)
ylabel("U2/E",fontsize=16)
legend(loc='upper right')
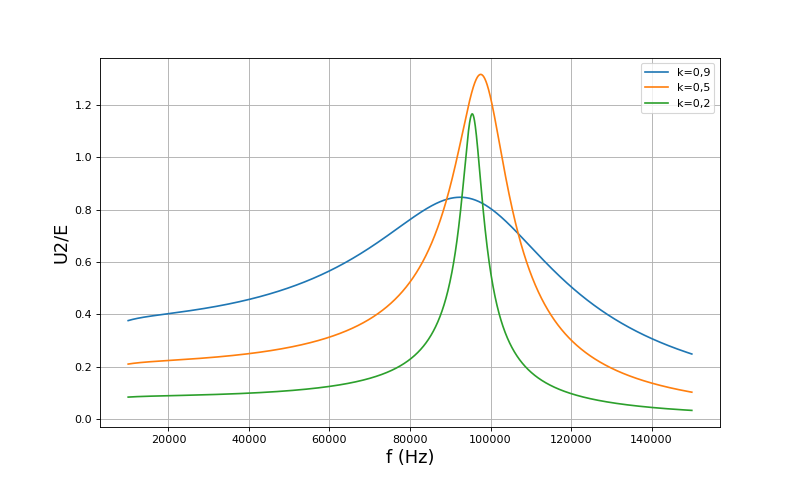 fig7.pdf
fig7.pdf
Ces courbent montrent que la fréquence de 70 kHz est un bon choix car elle permet d'avoir une augmentation régulière de l'amplitude de la tension aux bornes de la charge lorsque le coefficient de couplage augmente. Au contraire, le choix d'une fréquence proche de la résonance poserait problème car cette fréquence dépend du coefficient de couplage. Si l'on veut que le système puisse fonctionner à différentes valeurs de k, le choix d'une fréquence proche de 70 kHz s'impose. Si le coefficient de couplage est fixé (la distance entre les bobines de couplage est fixée), on pourra si nécessaire maximiser le transfert de puissance à la charge en choisissant une fréquence plus proche de la résonance de tension. Voyons ce qu'il en est pour une résistance de charge Rc=1 Ω :
Rc = 1
figure(figsize=(10,6))
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,0.9,r0,r1,r2,C1,rc1,Rc)
plot(f,np.absolute(U2),label='k=0,9')
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,0.5,r0,r1,r2,C1,rc1,Rc)
plot(f,np.absolute(U2),label='k=0,5')
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,0.2,r0,r1,r2,C1,rc1,Rc)
plot(f,np.absolute(U2),label='k=0,2')
grid()
xlabel("f (Hz)",fontsize=16)
ylabel("U2/E",fontsize=16)
legend(loc='upper right')
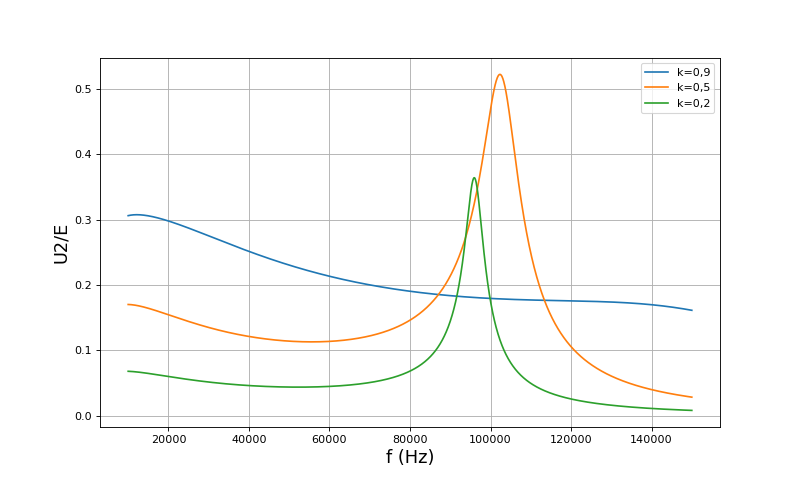 fig8.pdf
fig8.pdf
Pour cette résistance de charge petite, la fréquence de 70 kHz est toujours un bon choix.
Voici l'intensité du courant dans la bobine primaire et dans la charge en fonction du coefficient de couplage, pour la fréquence 70 kHz et pour une charge de 5 ohms :
Rc = 5
k_list = np.linspace(0,1,20)
I1_list = []
I2_list = []
phi1_list = []
f = np.array([70e3])
for k in k_list:
I0,I1,I2,U1,U2,P0,P1,P2 = couplage(f,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
I1_list.append(np.absolute(I1[0]))
I2_list.append(np.absolute(I2[0]))
phi1_list.append(np.angle(U1[0]/I1[0])*180/np.pi)
figure(figsize=(8,6))
plot(k_list,I1_list,label='I1')
plot(k_list,I2_list,label='I2')
xlabel('k',fontsize=16)
ylabel('I/E (A/V)',fontsize=16)
grid()
legend(loc='upper right')
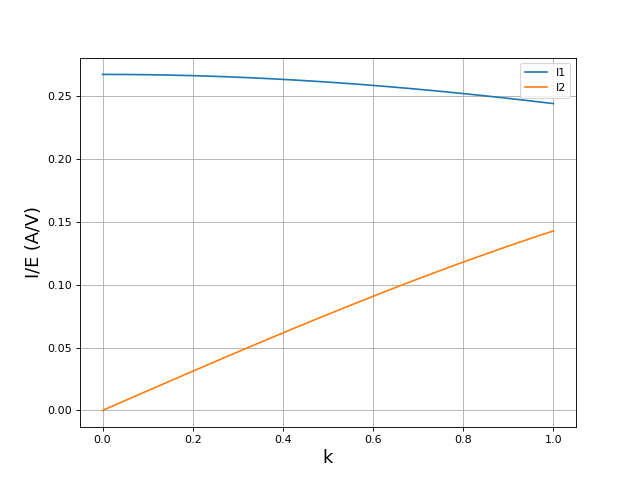 fig9.pdf
fig9.pdf
Voici la puissance dissipée dans la résistance de la bobine primaire (à ne pas confondre avec P1) et la puissance reçue par la charge :
P1_d = 0.5*r1*np.array(I1_list)**2
P2 = 0.5*Rc*np.array(I2_list)**2
figure(figsize=(6,4))
plot(k_list,P1_d,label="Bobine 1")
plot(k_list,P2,label='Charge')
xlabel('k',fontsize=16)
grid()
legend(loc='upper right')
ylabel(r"$P/E^2\ (\rm W/V^2)$",fontsize=16)
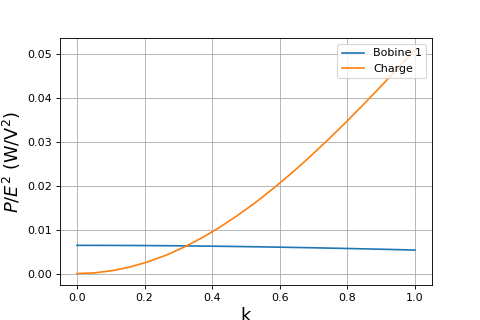 fig10.pdf
fig10.pdf
L'intensité du courant augmente de manière quasi linéaire avec le coefficient de couplage. L'intensité du courant dans la bobine primaire (I1) diminue un peu lorsque le couplage augmente. Or la puissance dissipée dans cette bobine est r1I12. Il s'en suit que cette puissance diminue un peu lorsqu'on augmente le couplage.
Voici le déphasage entre la tension et le courant pour la bobine primaire, en fonction du coefficient de couplage :
figure(figsize=(6,4))
plot(k_list,phi1_list)
xlabel('k',fontsize=16)
ylabel(r'$\phi_1\ (\rm deg)$',fontsize=16)
grid()
ylim(0,90)
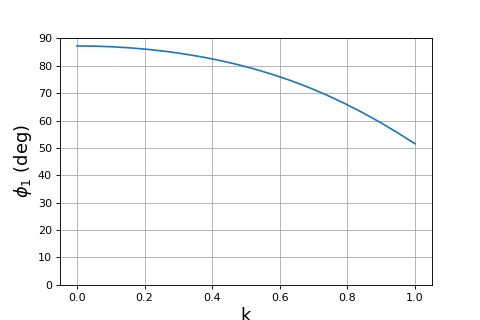 fig11.pdf
fig11.pdf
En réalité, la source de tension est un pont de transistors qui permet de délivrer, à partir d'une source de tension constante, une tension alternative de forme carrée. Si cette tension a une valeur moyenne nulle (obtenue avec un pont en H), le circuit précédent convient. En revanche, si la tension a une composante DC, c'est-à-dire une valeur moyenne positive, celle-ci conduirait à un courant dans les bobines 0 et 1, avec les pertes associées, sans aucun transfert d'énergie à la charge. Il faut donc éliminer la composante DC en rajoutant un condensateur de capacité C0 :
Figure pleine pageLa capacité C0 doit être assez grande pour ne pas modifier notablement la résonance étudiée précédemment (elle introduit une résonance sont la fréquence doit être plus basse). Voici la nouvelle fonction de calcul :
def couplage_C0(f,C0,rc0,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc):
M = k*np.sqrt(L1*L2)
w = 2*np.pi*f
N = len(f)
I0 = np.zeros(N,dtype=complex)
I1 = np.zeros(N,dtype=complex)
I2 = np.zeros(N,dtype=complex)
for i in range(N):
A = np.zeros((3,3),dtype=np.complex64)
A[0,0] = r0+1j*L0*w[i]+1/(1j*C1*w[i])+rc1+1/(1j*C0*w[i])+rc0
A[0,1] = -1/(1j*C1*w[i])-rc1
A[1,0] = r0+1j*L0*w[i]+1/(1j*C0*w[i])+rc0
A[1,1] = 1j*L1*w[i]+r1
A[1,2] = 1j*M*w[i]
A[2,1] = 1j*M*w[i]
A[2,2] = 1j*L2*w[i]+r2+Rc
B = np.array([1,1,0])
X = solve(A,B)
I0[i],I1[i],I2[i] = X[0],X[1],X[2]
P0 = 0.5*np.real(I0)
P2 = 0.5*Rc*np.absolute(I2)**2
U1 = r1+1j*L1*2*np.pi*f*I1
P1 = 0.5*np.real(I1*np.conjugate(U1))
U2 = Rc*I2
return I0,I1,I2,U1,U2,P0,P1,P2
Voyons si une capacité C0=1 μF convient, pour une charge Rc=5 Ω et un coefficient de couplage k=0,5 :
C0 = 1e-6 rc0 = 0.1 k = 0.5 Rc = 5 f = np.linspace(10e3,150e3,2000) I0,I1,I2,U1,U2,P0,P1,P2 = couplage_C0(f,C0,rc0,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc) trace(f,I0,I1,I2,U1,U2,P0,P1,P2)
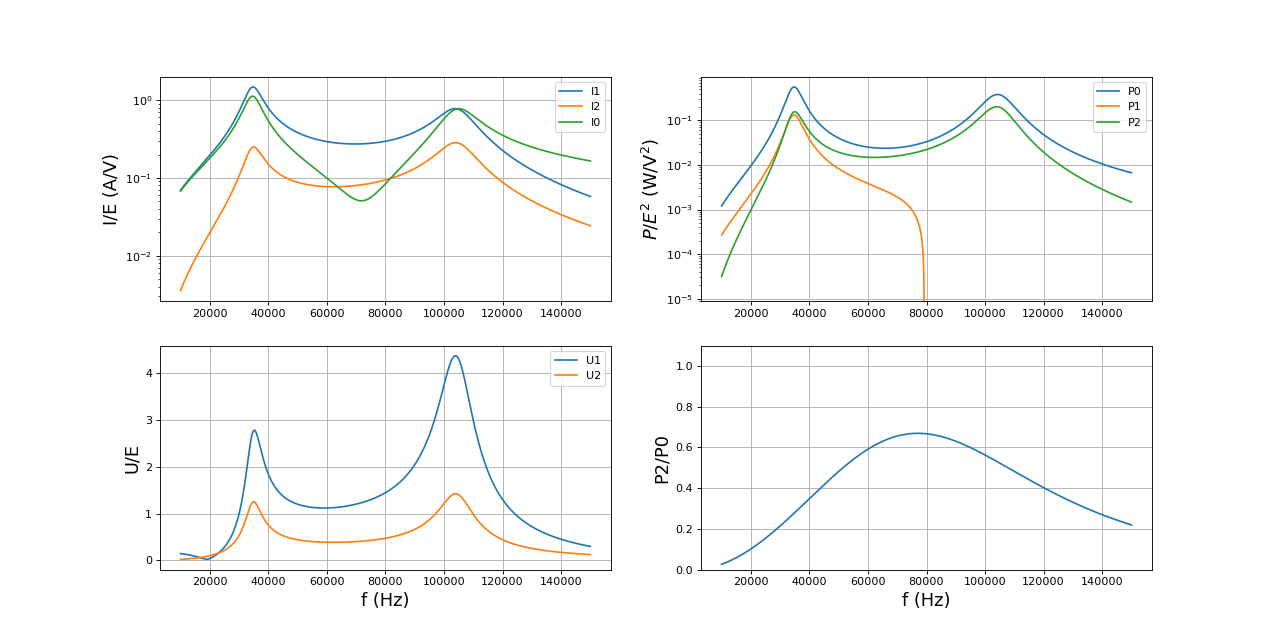 fig12.pdf
fig12.pdf
La résonance introduite par C0 a lieu vers 30 kHz et n'a que très peu d'effet sur le comportement à 70 kHz.
3. Étude expérimentale en régime sinusoïdal
Bien que dans l'utilisation réelle à forte puissance la tension d'entrée e(t) ne sera pas sinusoïdale (mais plutôt de forme carrée), seule une étude en régime sinusoïdal permet de comparer le modèle et le circuit réel.
Pour appliquer une tension e(t) sinusoïdale dont l'amplitude est de l'ordre du volt, on doit placer un amplificateur de puissance à la sortie du générateur de signaux. Nous utilisons un amplificateur réalisé avec l'ampli-op de puissance L165, qui peut fournir un courant jusqu'à 3 A. Voici le schéma de cet amplificateur :
Figure pleine pageIl s'agit d'un amplificateur de type non-inverseur, dont le gain en tension à basse fréquence est G=1+R2/R1. La résistance R2 est un potentiomètre, ce qui permet de faire varier le gain. Un gain de 2 convient pour cette expérience. Une double alimentation de laboratoire (de courant maximal 3 A) est utilisée pour l'alimentation de l'ampli-op.
L'expérience est réalisée sur le circuit sans condensateur C0, qui doit recevoir une tension alternative de valeur moyenne nulle. Voici tout d'abord U1/E en l'absence de charge, c'est-à-dire en l'absence de circuit secondaire. L'expérience est menée pour différentes valeurs de l'amplitude de la sinusoïde fournie par le générateur de signaux.
f = []
E = []
U1 = []
phi = []
for x in ["100mV","500mV","1V"]:
[a,b,c,d] = np.loadtxt('reponseFreq-L0=10u-Rc=inf-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U1.append(c)
phi.append(d)
# E : tension de CH1 par rapport à la tension programmée (100 mV)
# U1 : tension de CH2 par rapport à CH1
figure(figsize=(10,10))
subplot(211)
plot(f_ref/1e3,np.absolute(U1_ref),'k--',label='modele')
plot(f[0]/1e3,U1[0],label='experience E = 200 mV')
plot(f[1]/1e3,U1[1],label='experience E = 1 V')
plot(f[2]/1e3,U1[2],label='experience E = 2 V')
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U1/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
subplot(212)
plot(f_ref/1e3,np.angle(U1_ref)*180/np.pi,'k--',label='modele')
plot(f[0]/1e3,phi[0],label='experience E = 200 mV')
plot(f[1]/1e3,phi[1],label='experience E = 1 V')
plot(f[2]/1e3,phi[2],label='experience E = 2 V')
grid()
xlabel('f (kHz)',fontsize=16)
ylabel(r'$\phi_1$',fontsize=16)
legend(loc='upper right')
xlim(20,150)
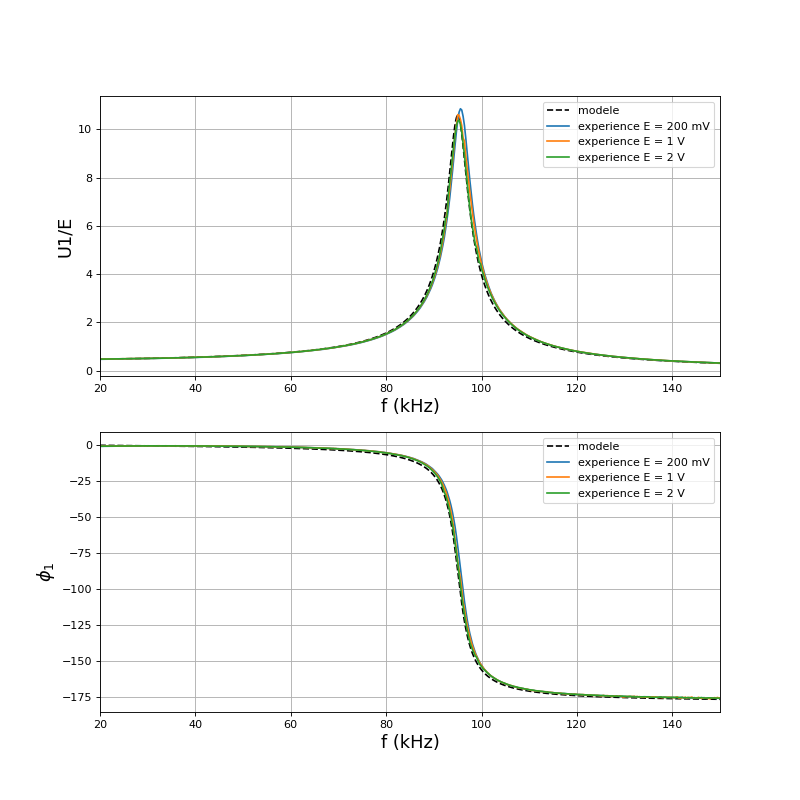 fig13.pdf
fig13.pdf
L'ajustement précis du modèle sur les courbes expérimentales (pour E égal à 1 ou 2 V) est obtenu d'une part en ajustant la valeur de L0 (qui détermine la fréquence de résonance), d'autre part en ajustant la résistance rC1, qui est le seul paramètre du modèle que nous n'avons pas mesuré indépendamment et qui a une influence sur la hauteur de la résonance. Celle-ci est en effet très sensible aux pertes dans le circuit.
Nous traçons les courbes de U1/E en fonction de la fréquence en présence du circuit secondaire, avec une résistance de charge de 5 ohms et pour différentes distances entre les deux bobines de couplage. Voici tout d'abord les courbes pour une distance d=0,9 mm entre les deux bobines de couplage. La courbe du modèle est obtenue en ajustant L1=L2 (pour la fréquence du maximum) et le coefficient de couplage k (pour sa hauteur). La nécessiter d'augmenter L1 vient du fait que la proximité de la plaque de ferrite de la bobine secondaire augmente notablement la valeur de l'auto-inductance de la bobine primaire (et réciproquement). Une mesure de l'auto-inductance avec un RLC-mètre donne en effet une valeur de 21,4 μH pour d=0,9 mm, 14,2 μH pour d=2,5 mm et 9,2 μH pour d=9,0 mm.
f = []
E = []
U1 = []
phi = []
for x in ["500mV","1V","2V"]:
[a,b,c,d] = np.loadtxt('reponseFreq-L0=10u-Rc=5-d=0,9-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U1.append(c)
phi.append(d)
L1 = L2 = 21.4e-6
r1 = r2 = 0.18
k = 0.93
Rc = 5
f_m = np.linspace(10e3,150e3,2000)
I0_m,I1_m,I2_m,U1_m,U2_m,P0_m,P1_m,P2_m = couplage(f_m,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure(figsize=(10,6))
plot(f[0]/1e3,U1[0],label='E = 1 V, d = 0,9 mm')
plot(f[1]/1e3,U1[1],label='E = 2 V, d = 0,9 mm')
plot(f[2]/1e3,U1[2],label='E = 3 V, d = 0,9 mm')
plot(f_m/1e3,np.absolute(U1_m),'k--',label='modele k=%0.2f'%k)
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U1/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,2)
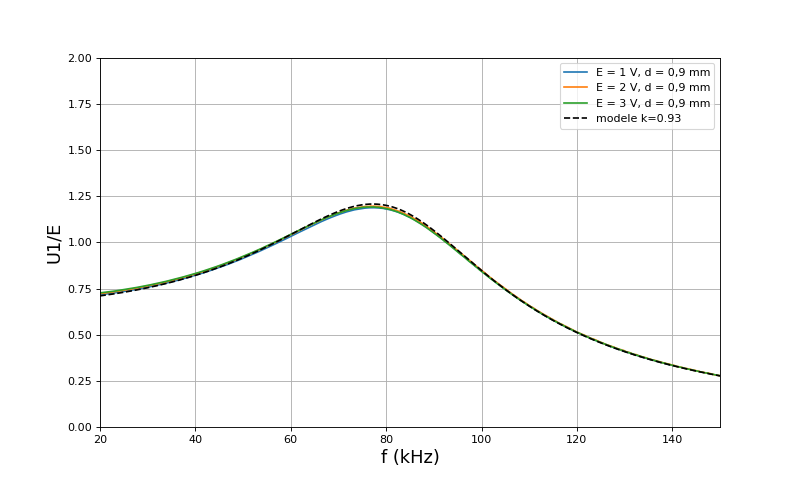 fig14.pdf
fig14.pdf
Voici les courbes pour une distance d=2,5 mm :
f = []
E = []
U1 = []
phi = []
for x in ["1V","2V"]:
[a,b,c,d] = np.loadtxt('reponseFreq-L0=10u-Rc=5-d=2,5-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U1.append(c)
phi.append(d)
L1 = L2 = 14.2e-6
k = 0.85
Rc = 5
f_m = np.linspace(10e3,150e3,2000)
I0_m,I1_m,I2_m,U1_m,U2_m,P0_m,P1_m,P2_m = couplage(f_m,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure(figsize=(10,6))
plot(f[0]/1e3,U1[0],label='E = 2 V, d = 2,5 mm')
plot(f[1]/1e3,U1[1],label='E = 4 V, d = 2,5 mm')
plot(f_m/1e3,np.absolute(U1_m),'k--',label='modele k=%0.2f'%k)
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U1/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,2)
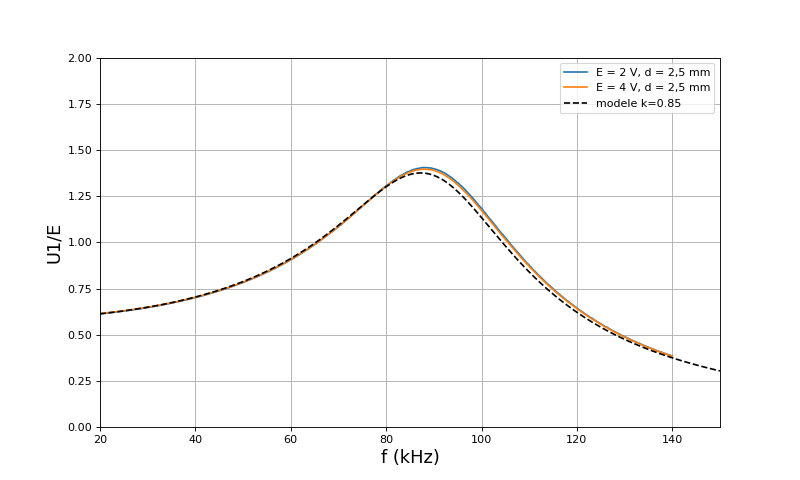 fig15.pdf
fig15.pdf
Voici les courbes pour une distance d=9 mm :
f = []
E = []
U1 = []
phi = []
for x in ["500mV","1V","1,5V"]:
[a,b,c,d] = np.loadtxt('reponseFreq-L0=10u-Rc=5-d=9-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U1.append(c)
phi.append(d)
L1 = L2 = 9.2e-6
k = 0.46
Rc = 5
f_m = np.linspace(10e3,150e3,2000)
I0_m,I1_m,I2_m,U1_m,U2_m,P0_m,P1_m,P2_m = couplage(f_m,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure(figsize=(10,6))
plot(f[0]/1e3,U1[0],label='E = 1 V, d = 9 mm')
plot(f[1]/1e3,U1[1],label='E = 2 V, d = 9 mm')
plot(f[1]/1e3,U1[2],label='E = 3 V, d = 9 mm')
plot(f_m/1e3,np.absolute(U1_m),'k--',label='modele k=%0.2f'%k)
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U1/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,5)
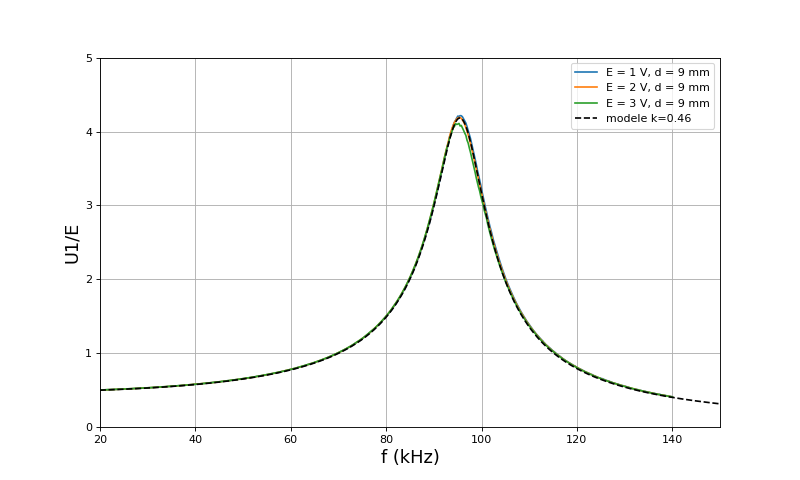 fig16.pdf
fig16.pdf
Voici les courbes de U2/E en fonction de la fréquence, pour d=0,9 mm :
f = []
E = []
U2 = []
phi = []
for x in ["1V","2V","4V"]:
[a,b,c,d] = np.loadtxt('reponseFreqU2-L0=10u-Rc=5-d=0,9-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U2.append(c)
phi.append(d)
L1 = L2 = 21.4e-6
k = 0.93
Rc = 5
f_m = np.linspace(10e3,150e3,2000)
I0_m,I1_m,I2_m,U1_m,U2_m,P0_m,P1_m,P2_m = couplage(f_m,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure(figsize=(10,6))
plot(f[0]/1e3,U2[0],label='E = 2 V, d = 0,9 mm')
plot(f[1]/1e3,U2[1],label='E = 4 V, d = 0,9 mm')
plot(f[1]/1e3,U2[2],label='E = 6 V, d = 0,9 mm')
plot(f_m/1e3,np.absolute(U2_m),'k--',label='modele k=%0.2f'%k)
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U2/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,2)
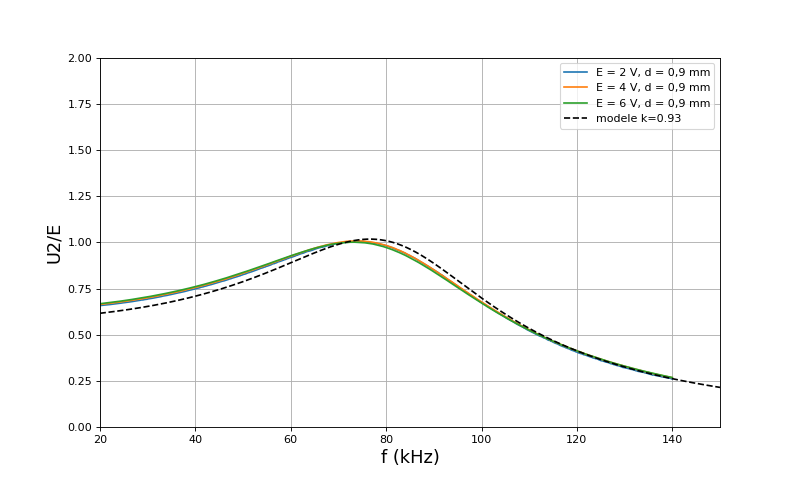 fig17.pdf
fig17.pdf
Voici les courbes de U2/E en fonction de la fréquence, pour d=2,5 mm :
f = []
E = []
U2 = []
phi = []
for x in ["1V","2V","4V"]:
[a,b,c,d] = np.loadtxt('reponseFreqU2-L0=10u-Rc=5-d=2,5-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U2.append(c)
phi.append(d)
L1 = L2 = 14.2e-6
k = 0.85
Rc = 5
f_m = np.linspace(10e3,150e3,2000)
I0_m,I1_m,I2_m,U1_m,U2_m,P0_m,P1_m,P2_m = couplage(f_m,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure(figsize=(10,6))
plot(f[0]/1e3,U2[0],label='E = 2 V, d = 2,5 mm')
plot(f[1]/1e3,U2[1],label='E = 4 V, d = 2,5 mm')
plot(f[1]/1e3,U2[2],label='E = 6 V, d = 2,5 mm')
plot(f_m/1e3,np.absolute(U2_m),'k--',label='modele k=%0.2f'%k)
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U2/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,2)
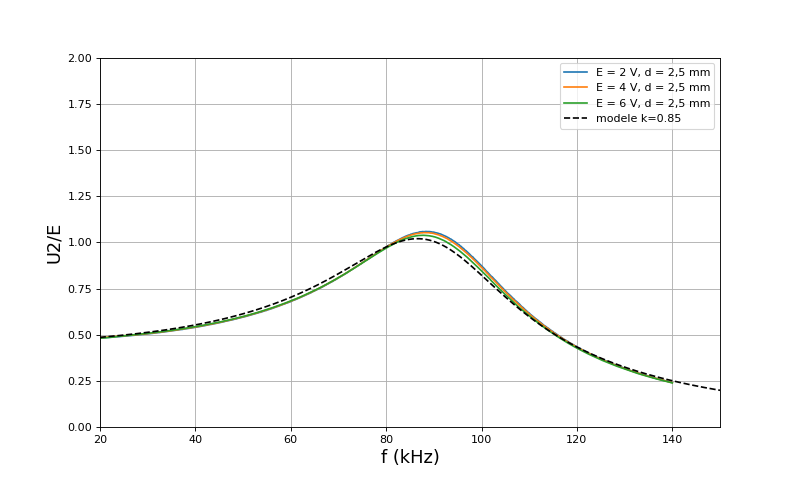 fig18.pdf
fig18.pdf
Voici les courbes de U2/E en fonction de la fréquence, pour d=9 mm :
f = []
E = []
U2 = []
phi = []
for x in ["500mV","1V","1,5V"]:
[a,b,c,d] = np.loadtxt('reponseFreqU2-L0=10u-Rc=5-d=9-%s.csv'%x,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U2.append(c)
phi.append(d)
L1 = L2 = 9.2e-6
k = 0.46
Rc = 5
f_m = np.linspace(10e3,150e3,2000)
I0_m,I1_m,I2_m,U1_m,U2_m,P0_m,P1_m,P2_m = couplage(f_m,L0,L1,L2,k,r0,r1,r2,C1,rc1,Rc)
figure(figsize=(10,6))
plot(f[0]/1e3,U2[0],label='E = 1 V, d = 9 mm')
plot(f[1]/1e3,U2[1],label='E = 2 V, d = 9 mm')
plot(f[1]/1e3,U2[2],label='E = 3 V, d = 9 mm')
plot(f_m/1e3,np.absolute(U2_m),'k--',label='modele k=%0.2f'%k)
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U2/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,2)
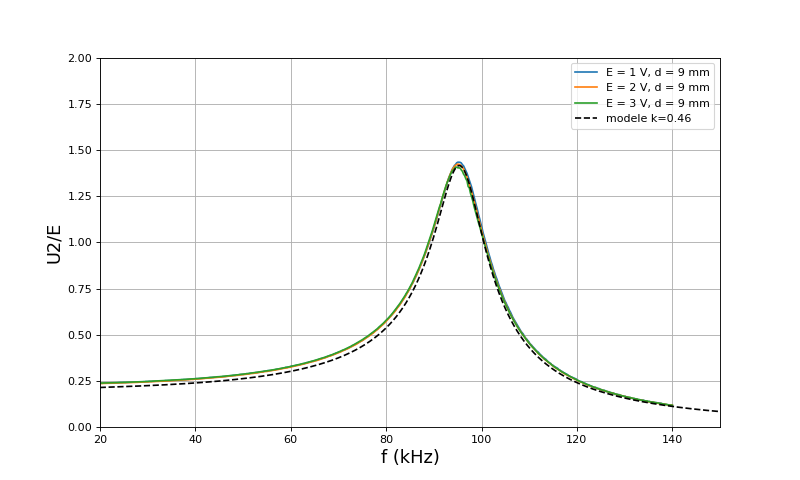 fig19.pdf
fig19.pdf
Ces courbes montrent un bon accord entre le modèle et les résultats expérimentaux, par ajustement de L1=L2 et du coefficient de couplage k.
Voici, pour E=2 V, les courbes de U2/E en fonction de la fréquence pour les trois distances :
f = []
E = []
U2 = []
phi = []
for d in ["0,9","2,5","9"]:
[a,b,c,d] = np.loadtxt('reponseFreqU2-L0=10u-Rc=5-d=%s-1V.csv'%d,unpack=True,skiprows=1,delimiter=',')
f.append(a)
E.append(b)
U2.append(c)
phi.append(d)
figure(figsize=(10,6))
plot(f[0]/1e3,U2[0],label='E = 1 V, d = 0,9 mm')
plot(f[1]/1e3,U2[1],label='E = 1 V, d = 2,5 mm')
plot(f[1]/1e3,U2[2],label='E = 1 V, d = 9 mm')
grid()
xlabel('f (kHz)',fontsize=16)
ylabel('U2/E',fontsize=16)
legend(loc='upper right')
xlim(20,150)
ylim(0,2)
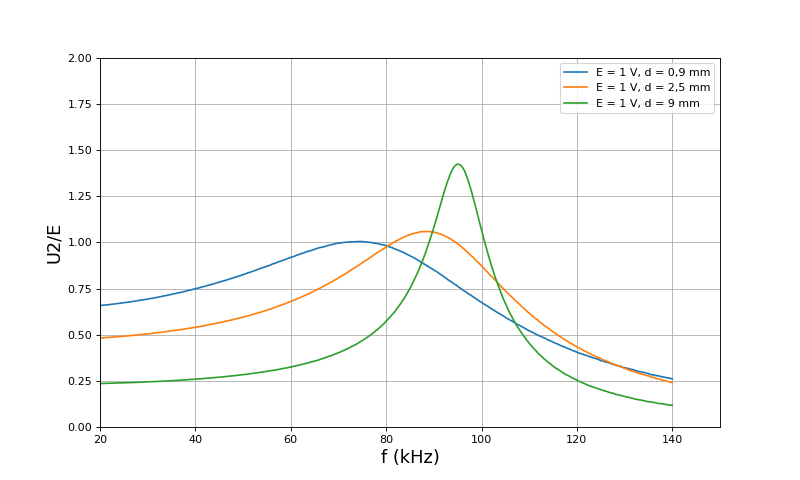 fig20.pdf
fig20.pdf
Ces courbes confirment la conclusion établie avec le modèle : la fréquence devra être choisie au plus à 70 kHz, afin que l'amplitude de la tension aux bornes de la charge augmente régulièrement lorsqu'on rapproche les deux bobines. Les fréquences trop proches de la résonance de tension sont à éviter car cette fréquence dépend justement du coefficient de couplage.
La vidéo ci-dessous montre la tension e(t) (en jaune) et la tension u2(t) (en bleu) au cours d'un déplacement manuel de la bobine secondaire. La fréquence est 70 kHz et E=2 V.
La vidéo ci-dessous montre la tension e(t) (en jaune) et la tension u1(t) (en bleu) au cours d'un déplacement manuel de la bobine secondaire. La fréquence est 70 kHz et E=2 V.
La tension u2(t) (aux bornes de la bobine primaire) présente un déphasage notable par rapport à e(t) lorsque la distance entre les deux bobines est inférieure à 1 cm. Ce déphasage pourra servir à détecter l'éloignement du circuit secondaire (ou la déconnexion de la charge) et de déclencher en conséquence l'arrêt de l'alimentation.
4. Conversion DC-AC avec pont MOSFET
L'objectif est de transmettre une puissance entre une source de tension constante et la charge. Un pont MOSFET est utilisé pour convertir la tension Vs de la source en tension e(t) alternative. Dans cette partie, on présente une simulation SPICE du système complet, comportant le pont de transistors, le circuit primaire et le circuit secondaire.
Voici le schéma du circuit de la simulation :
Figure pleine pageLe pont est constitué de quatre transistors MOSFET. Le modèle de ces transistors est celui de l'IRF50R500CE (Infineon). Les transistors Q2 et Q3 sont pilotés par une source de tension PULSE (V2) qui délivre un signal carré de 0 à 30 V, de rapport cyclique 1/2 et dont la période est donnée en microsecondes (14 us sur le schéma ci-dessus). Les transistors Q1 et Q4 sont pilotés par une source de tension PULSE (V3) qui délivre le signal carré complémentaire du premier. La source de tension est Vs=10 V (V1 sur le schéma). Pour rendre un transistor passant, nous appliquons une tension de grille de 30 V par rapport à la masse. Sachant que la tension d'une sortie du pont (OUT1 ou OU2) atteint Vs lorsque le transistor du haut (Q1 ou Q3) est passant, la tension de grille de ce transistor doit être plus grande d'au moins 10 V par rapport à Vs. Avec une tension de grille (par rapport à la masse) de 30 V, on peut donc augmenter Vs jusqu'à 20 V.
Le circuit primaire, modélisé précédemment en régime sinusoïdal, est branché entre les sorties OUT1 et OUT2 du pont. Il faut remarquer qu'aucune de ces deux sorties ne peut être reliée à la masse puisque la tension e(t)=OUT1-OUT2 est alternative. En conséquence, la tension v2(t) aux bornes de la bobine primaire (d'inductance L2 sur le schéma), est obtenue par différence des tensions à ses bornes.
Les simulations ci-dessous sont faites avec LTSpice, pour une période de 14 microsecondes (fréquence 71 kHz) et pour différentes valeurs du coefficient de couplage. Les tensions e(t) et u1(t) ne peuvent pas être obtenues directement par pointé sur le schéma car il s'agit de tensions différentielles entre deux nœuds.
[t,V005,V006,V007,V008] = np.loadtxt('pontMOSFET-spice-14us-k=0,99.txt',unpack=True,skiprows=1)
e = V005-V006
u1 = V007-V006
u2 = V008
t *= 1e6
T = 20e-3
u1_eff = [u1.std()]
u2_eff = [u2.std()]
freq = [1/T]
figure(figsize=(12,6))
title("T = 14us, k = 0.99")
plot(t,e,label='e')
plot(t,u1,label='u1')
plot(t,u2,label='u2')
xlabel("t (us)",fontsize=16)
ylabel("U (V)",fontsize=16)
grid()
ylim(-15,15)
xlim(50,100)
legend(loc='upper right',fontsize=16)
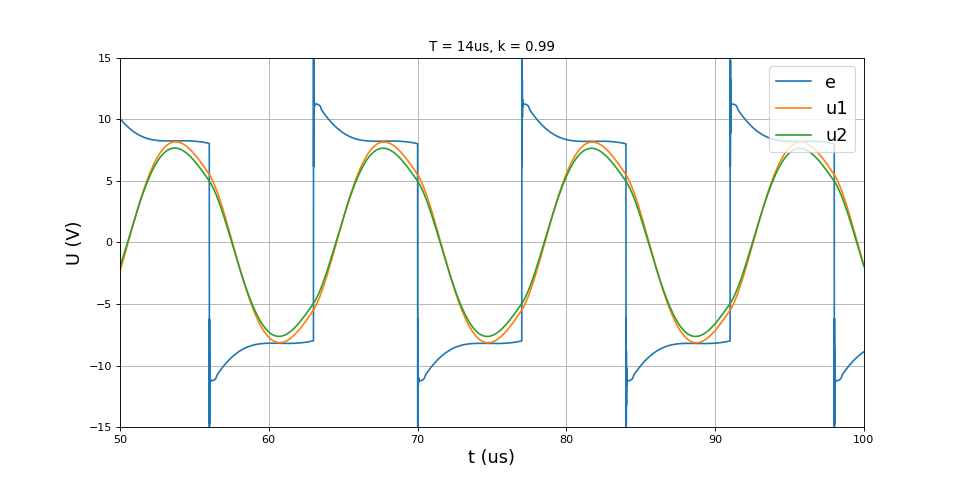 fig21.pdf
fig21.pdf
[t,V005,V006,V007,V008] = np.loadtxt('pontMOSFET-spice-14us-k=0,9.txt',unpack=True,skiprows=1)
e = V005-V006
u1 = V007-V006
u2 = V008
t *= 1e6
T = 20e-3
u1_eff = [u1.std()]
u2_eff = [u2.std()]
freq = [1/T]
figure(figsize=(12,6))
title("T = 14us, k = 0.9")
plot(t,e,label='e')
plot(t,u1,label='u1')
plot(t,u2,label='u2')
xlabel("t (us)",fontsize=16)
ylabel("U (V)",fontsize=16)
grid()
ylim(-15,15)
xlim(50,100)
legend(loc='upper right',fontsize=16)
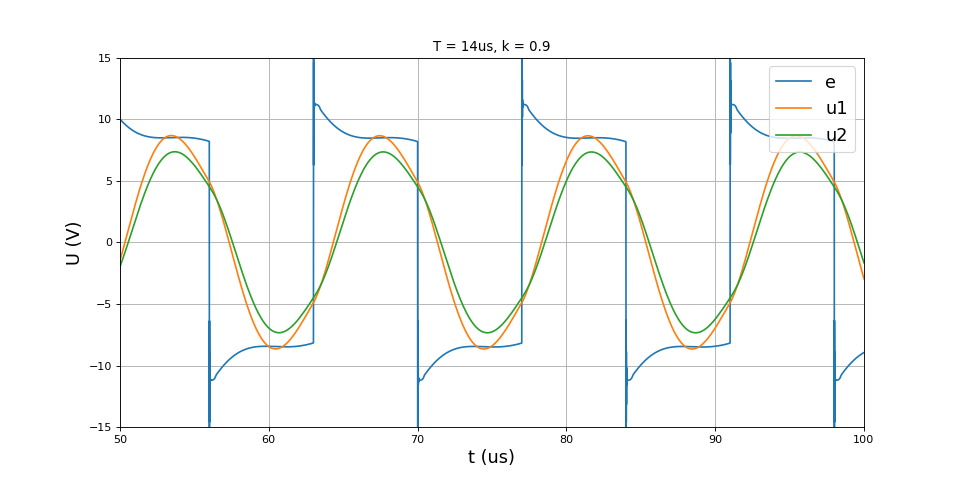 fig22.pdf
fig22.pdf
[t,V005,V006,V007,V008] = np.loadtxt('pontMOSFET-spice-14us-k=0,8.txt',unpack=True,skiprows=1)
e = V005-V006
u1 = V007-V006
u2 = V008
t *= 1e6
T = 20e-3
u1_eff = [u1.std()]
u2_eff = [u2.std()]
freq = [1/T]
figure(figsize=(12,6))
title("T = 14us, k = 0.8")
plot(t,e,label='e')
plot(t,u1,label='u1')
plot(t,u2,label='u2')
xlabel("t (us)",fontsize=16)
ylabel("U (V)",fontsize=16)
grid()
ylim(-15,15)
xlim(50,100)
legend(loc='upper right',fontsize=16)
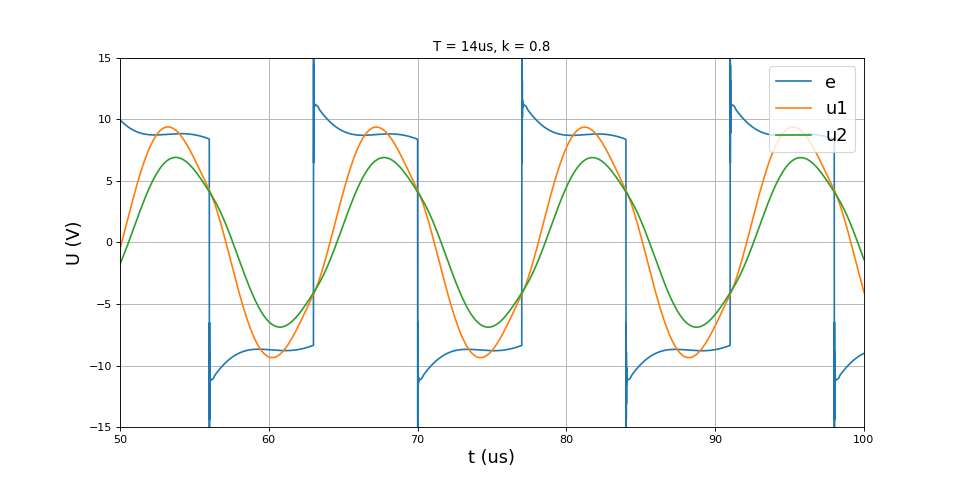 fig23.pdf
fig23.pdf
[t,V005,V006,V007,V008] = np.loadtxt('pontMOSFET-spice-14us-k=0,5.txt',unpack=True,skiprows=1)
e = V005-V006
u1 = V007-V006
u2 = V008
t *= 1e6
T = 20e-3
u1_eff = [u1.std()]
u2_eff = [u2.std()]
freq = [1/T]
figure(figsize=(12,6))
title("T = 14us, k = 0.5")
plot(t,e,label='e')
plot(t,u1,label='u1')
plot(t,u2,label='u2')
xlabel("t (us)",fontsize=16)
ylabel("U (V)",fontsize=16)
grid()
ylim(-15,15)
xlim(50,100)
legend(loc='upper right',fontsize=16)
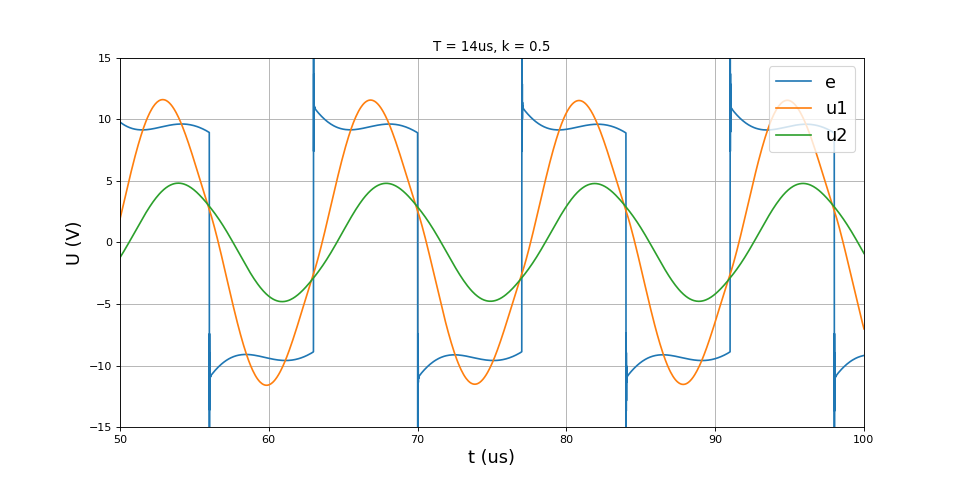 fig24.pdf
fig24.pdf
[t,V005,V006,V007,V008] = np.loadtxt('pontMOSFET-spice-14us-k=0,2.txt',unpack=True,skiprows=1)
e = V005-V006
u1 = V007-V006
u2 = V008
t *= 1e6
T = 20e-3
u1_eff = [u1.std()]
u2_eff = [u2.std()]
freq = [1/T]
figure(figsize=(12,6))
title("T = 14us, k = 0.2")
plot(t,e,label='e')
plot(t,u1,label='u1')
plot(t,u2,label='u2')
xlabel("t (us)",fontsize=16)
ylabel("U (V)",fontsize=16)
grid()
ylim(-15,15)
xlim(50,100)
legend(loc='upper right',fontsize=16)
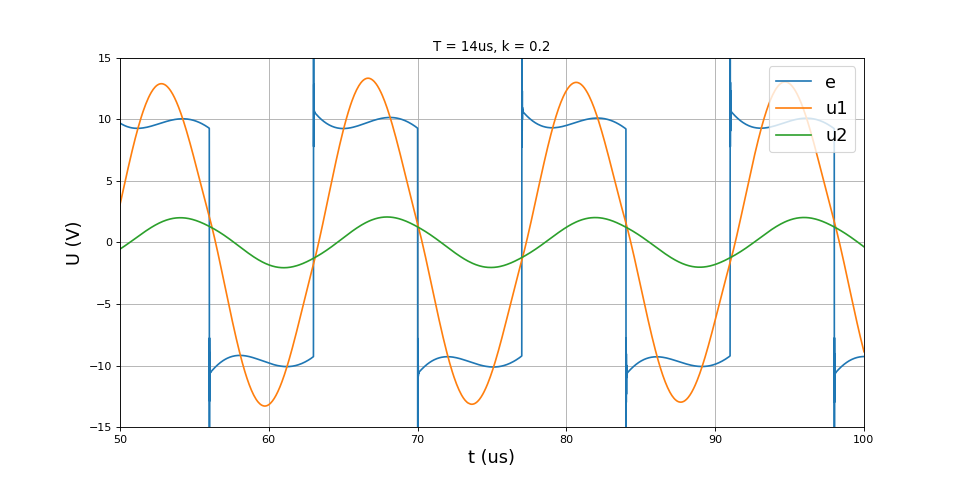 fig25.pdf
fig25.pdf
Voici, pour un coefficient de couplage k=0,99, la tension aux bornes de la bobine primaire, le courant qui la traverse et le produit des deux, qui est la puissance reçue par cette bobine :
[t,V006,V007,IL2] = np.loadtxt('pontMOSFET-spice-14us-k=0,99-U2-IL2.txt',unpack=True,skiprows=1)
u1 = V007-V006
i1 = IL2
t *= 1e6
figure(figsize=(12,10))
subplot(311)
plot(t,u1)
ylabel(r"$u_1\ (\rm V)$",fontsize=16)
grid()
subplot(312)
plot(t,i1)
ylabel(r"$I_1\ (\rm A)$",fontsize=16)
grid()
subplot(313)
P1 = u1*i1
plot(t,P1)
ylim(-20,20)
grid()
ylabel(r"$u_1i_1\ (\rm W)$",fontsize=16)
xlabel("t (us)")
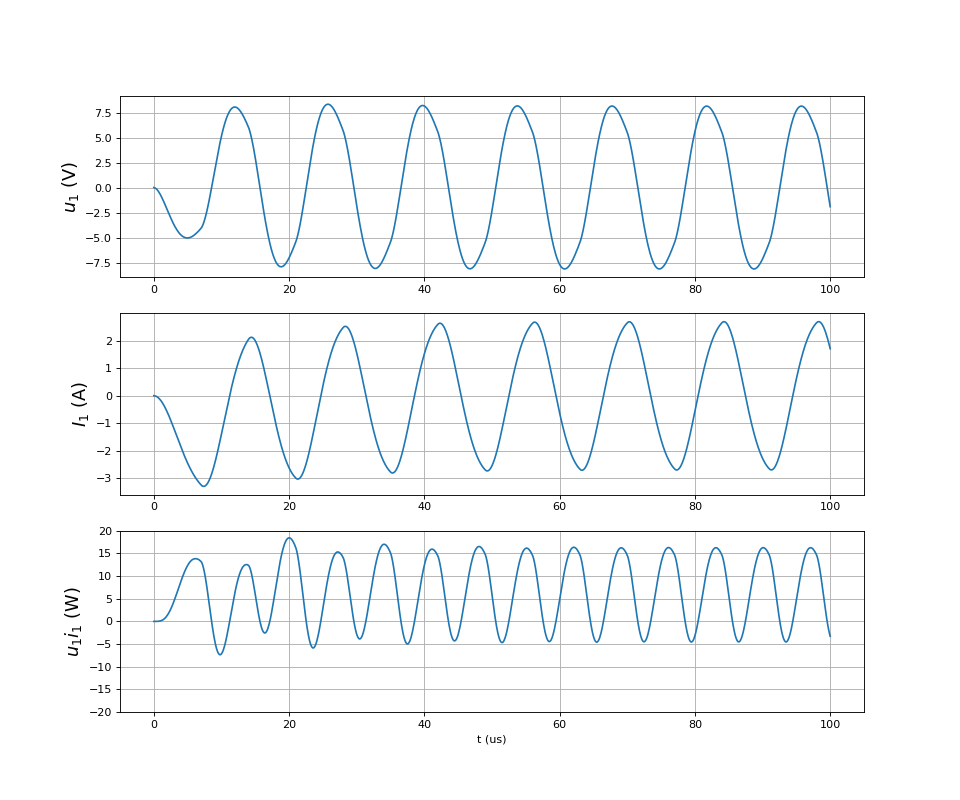 fig26.pdf
fig26.pdf
print(P1.mean()) --> 11.74086550612374
La puissance moyenne reçue par la bobine primaire est positive. Cette puissance moyenne est la somme de la puissance dissipée dans les deux bobines et de la puissance transmise à la charge.
5. Étude expérimentale à forte puissance
La source de tension constante est une alimentation de laboratoire de tension maximale 30 V et de courant maximal 3 A. L'alimentation est configurée en source de tension et on note Vs sa tension. La tension e(t) en entrée du circuit primaire est obtenue par découpage au moyen d'un pont en H à transistors MOSFET. Nous utilisons le pont intégré L6203 (ST Microelectronic), qui peut délivrer jusqu'à 4 A à une fréquence de 100 kHz. Voici le schéma interne du L6203 :

L'entrée IN1 commande le demi-pont à gauche, l'entrée IN2 celui de droite. L'entrée ENABLE active le pont. La figure suivante montre les deux configurations du pont que nous allons utiliser :
Figure pleine pageLorsque IN1=1 et IN2=0, on a e(t)=-Vs (si rien n'est branché entre OUT1 et OUT2). Lorsque IN1=0 et IN2=1, on a e(t)=Vs. La tension Vs minimale est d'environ 9 V. Si ENABLE=0, tous les transistors sont à l'état bloqué (interruteurs ouverts) quels que soient les états de IN1 et IN2. Remarquons que ce pont est souvent utilisé pour alimenter un moteur à courant continu; dans ce cas, on fixe le sens du passage du courant avec IN1 et IN2 et on applique le signal à rapport cyclique variable sur ENABLE.
L'utilisation de ce pont pour générer une tension e(t) alternative nécessite donc d'appliquer sur IN1 et IN2 deux signaux complémentaires. Pour y parvenir, on peut générer deux signaux complémentaires avec un Timer (voir Pilotage d'un pont L298) ou bien utiliser une porte logique NON. La première solution s'impose si on veut contrôler les rapports cycliques de IN1 et IN2 indépendamment. Dans le cas présent, le rapport cyclique de e(t) vaut 1/2 et, compte tenu de la vitesse de commutation du pont, l'utilisation d'une porte logique convient. Voici le schéma du L6203 avec la porte NON et les deux entrées de l'Arduino MEGA utilisées pour le pilotage. Le L6203 ne nécessite pas d'alimentation 5 V mais le LS7404 (quadruple porte NON) en nécessite une, que nous prenons sur la carte Arduino (laquelle est alimentée par USB). La résistance de 0,2 Ω permet d'accéder au courant circulant dans la charge.
Figure pleine pageLa génération de deux signaux complémentaires avec un Timer est expliqué dans Pilotage d'un pont L298. Le programme Arduino ci-dessous (pour Arduino MEGA) génère un signal de rapport cyclique 0,5 sur D11 et un signal complémentaire sur D12. Si on utilise la porte NON, la sortie D12 n'est pas utilisée; dans le cas contraire, D12 est branchée sur l'entrée IN2 du L6203.
#include <Arduino.h>
#define IN1 11 // PB5 (OC1A)
#define IN2 12 // PB6 (OC1B)
#define ENA 8
volatile uint32_t count;
uint32_t max_count;
uint16_t diviseur[6] = {0,1,8,64,256,1024};
uint32_t icr;
uint8_t tccr1a,tccr1b;
uint16_t ocr1a,ocr1b;
bool inter;
void config_impulsions(float period, int32_t nombre, float ra, float rb) {
/*
periode : T en microsecondes
nombre : nombre de cyles (nombre de cycles illimité si nombre==0)
ra : rapport cyclique de OC1A
rb : rapport cyclique de OC1B
*/
count = 0;
if (nombre >0) {
max_count = nombre+1;
inter = true;
}
else inter = false;
tccr1a = 0;
tccr1b = 0;
//phase and frequency correct PWM mode, top = ICR1 WGM3:0 = 1,0,0,0
tccr1b |= (1 << WGM13);
// COM1A1 = 1, COM1A0 = 0 : clear OC1A on compare match when up counting
// COM1B1 = 1, COM1B0 = 1 : set OC1B on compare match when up counting
tccr1a |= (1 << COM1A1) | (1 << COM1B1) | (1 << COM1B0);
icr = (F_CPU/1000000*period/2);
int d = 1;
while ((icr>0xFFFF)&&(d<5)) {
d++;
icr = (F_CPU/1000000*period/2/diviseur[d]);
}
tccr1b |= d;
ocr1a = icr*ra;
ocr1b = icr*(1.0-rb);
}
void start_impulsions() {
cli();
count = 0;
TCCR1A = tccr1a;
TCCR1B = tccr1b;
TCNT1 = 0;
ICR1 = icr;
OCR1A = ocr1a;
OCR1B = ocr1b;
if (inter) TIMSK1 = 1 << TOIE1; // overflow interrupt enable
sei();
}
ISR(TIMER1_OVF_vect) {
count++;
if (count==max_count) {
TCCR1A = 0;
PORTB &= ~((1 << PORTB5) | (1 << PORTB6)); // PB5 et PB6 LOW
}
}
void setup() {
pinMode(IN1,OUTPUT);
pinMode(IN2,OUTPUT);
PORTB &= ~(1 << PORTB5);
PORTB &= ~(1 << PORTB6);
pinMode(ENA,OUTPUT);
digitalWrite(ENA,HIGH);
config_impulsions(13,0,0.5,0.5);
start_impulsions();
}
void loop() {
}
Voici les tensions e(t) (en sortie du pont) et u2(t) pour une distance d=20 mm et trois périodes différentes. On indique aussi le courant moyen débité par la l'alimentation. La tension de celle-ci est Vs=10 V.
figure(figsize=(10,10))
subplot(311)
[t,e,u2] = np.loadtxt('pontMOSFET-E-U2-14us-d=20mm.csv',skiprows=1,unpack=True,delimiter=',')
t *= 1e6
U2_eff_a = u2.std()
title("T = 14 us (71 kHz), Is = 168 mA")
plot(t,u2,label=r"$u_2(t)$")
plot(t,e,label="e(t)")
legend(loc='upper right')
grid()
subplot(312)
[t,e,u2] = np.loadtxt('pontMOSFET-E-U2-16us-d=20mm.csv',skiprows=1,unpack=True,delimiter=',')
t *= 1e6
U2_eff_b = u2.std()
title("T = 16 us (62 kHz), Is = 164 mA")
plot(t,u2,label=r"$u_2(t)$")
plot(t,e,label="e(t)")
legend(loc='upper right')
grid()
subplot(313)
[t,e,u2] = np.loadtxt('pontMOSFET-E-U2-18us-d=20mm.csv',skiprows=1,unpack=True,delimiter=',')
t *= 1e6
U2_eff_c = u2.std()
title("T = 18 us (55 kHz), Is = 215 mA")
plot(t,u2,label=r"$u_2(t)$")
plot(t,e,label="e(t)")
xlabel(r"$t\ (\rm \mu s)$",fontsize=16)
ylabel("Volts",fontsize=16)
legend(loc='upper right')
grid()
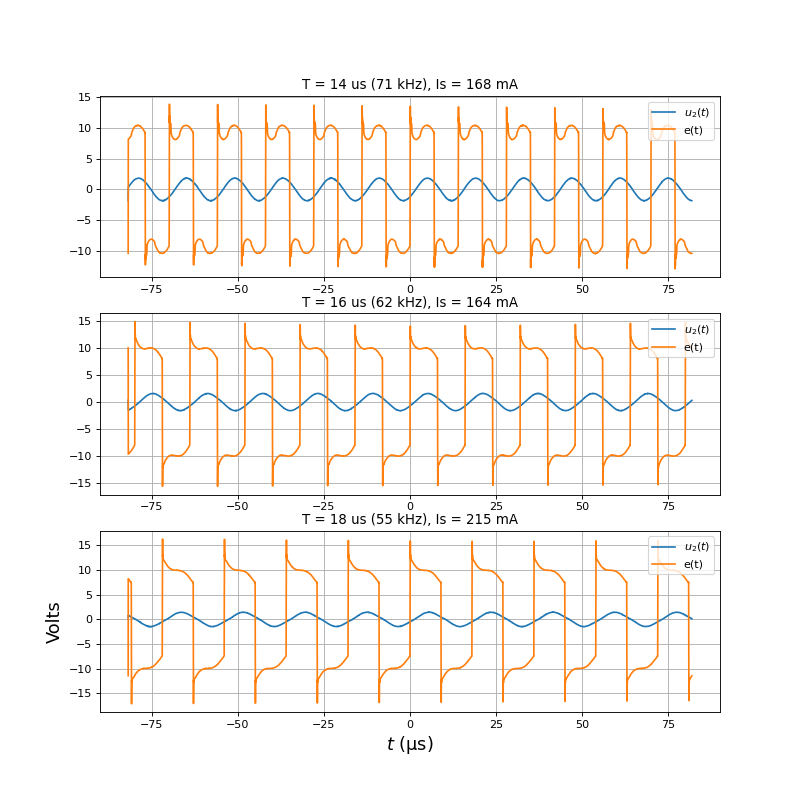 fig27.pdf
fig27.pdf
Voici les puissance moyennes reçues par la charge pour les trois fréquences :
print([U2_eff_a**2/Rc,U2_eff_b**2/Rc,U2_eff_c**2/Rc]) --> [0.33507805881352837, 0.2401136328251306, 0.19073660439757872]
et les puissance moyennes fournies par l'alimentation :
print([10*0.168,10*0.164,10*0.215]) --> [1.6800000000000002, 1.6400000000000001, 2.15]
Comme prévu par la simulation, la fréquence de 71 kHz (proche de 70 kHz) donne la plus grande puissance transmise à la charge. On peut déterminer un rendement, défini comme la puissance reçue par la charge sur la puissance fournie par l'alimentation. Bien sûr, ce rendement n'est pas comparable au rendement calculé dans le modèle car il dépend aussi des pertes dans le pont de transistors. Les rendements pour les trois fréquences sont 0.2, 0.15 et 0.088. La fréquence de 71 kHz est donc de loin celle qui donne le meilleur rendement, conformément aux résultats du modèle. Nous optons donc pour la période de 14 us (fréquence 71 kHz).
Voici les tensions e(t) et u2(t) pour d=10 mm (plus ou moins 1 mm) :
figure(figsize=(10,6))
[t,e,u2] = np.loadtxt('pontMOSFET-E-U2-14us-d=10mm.csv',skiprows=1,unpack=True,delimiter=',')
t *= 1e6
U2_eff_a = u2.std()
title("T = 14 us (71 kHz), Is = 418 mA")
plot(t,u2,label=r"$u_2(t)$")
plot(t,e,label="e(t)")
legend(loc='upper right')
xlabel(r"$t\ (\rm \mu s)$",fontsize=16)
ylabel("Volts",fontsize=16)
xlim(-50,50)
grid()
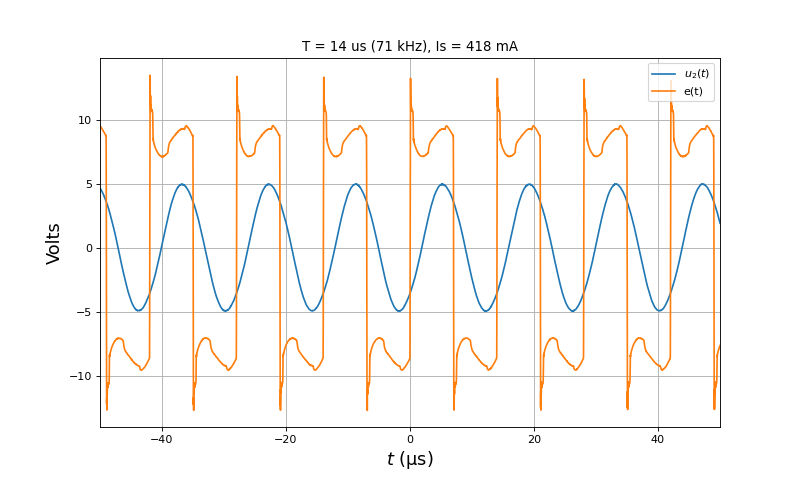 fig28.pdf
fig28.pdf
Puissance transmise à la charge :
print(U2_eff_a**2/Rc) --> 2.4496887778437393
Le rendement (par rapport à l'alimentation) est :
print(U2_eff_a**2/Rc/(10*0.418)) --> 0.5860499468525693
Voici les tensions e(t) et u2(t) pour d=2,5 mm :
figure(figsize=(10,6))
[t,e,u2] = np.loadtxt('pontMOSFET-E-U2-14us-d=2,5mm.csv',skiprows=1,unpack=True,delimiter=',')
t *= 1e6
U2_eff_a = u2.std()
title("T = 14 us (71 kHz), Is = 921 mA")
plot(t,u2,label=r"$u_2(t)$")
plot(t,e,label="e(t)")
legend(loc='upper right')
xlabel(r"$t\ (\rm \mu s)$",fontsize=16)
ylabel("Volts",fontsize=16)
xlim(-50,50)
grid()
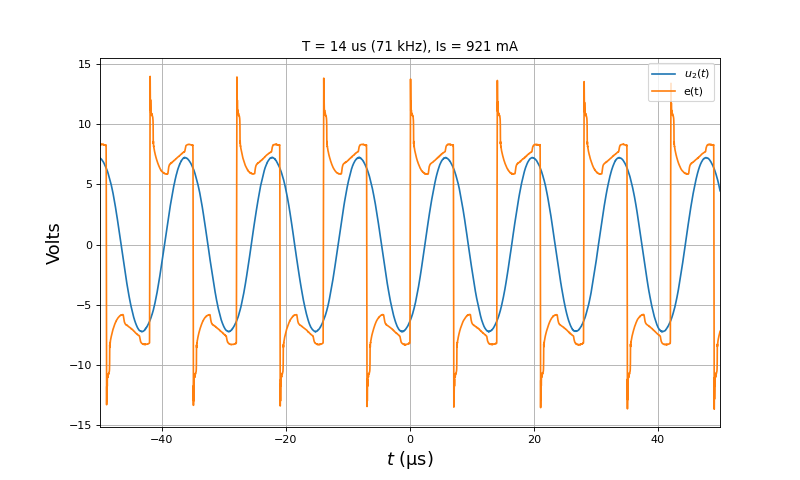 fig29.pdf
fig29.pdf
Puissance transmise à la charge :
print(U2_eff_a**2/Rc) --> 5.4408466814591145
Le rendement (par rapport à l'alimentation) est :
print(U2_eff_a**2/Rc/(10*0.921)) --> 0.5907542542300884
La vidéo ci-dessous montre la tension e(t) (en jaune) et la tension u2(t) (en bleu) au cours d'un déplacement manuel de la bobine secondaire. La fréquence est 71 kHz.
Afin de savoir s'il est possible d'obtenir une information sur la présence du circuit secondaire (avec la charge), nous visualisons le signal de commande (sortie D11 de l'Arduino) et la tension u2(t) :
Comme constaté plus haut en régime sinusoïdal, le déphasage entre u2(t) et le signal de commande augmente avec le couplage, mais seulement lorsque la distance entre les deux bobines est inférieure à 10 mm. Si le système doit fonctionner à une distance inférieure à 10 mm (condition pour avoir un rendement acceptable), on pourra ajouter un comparateur de phase constitué d'un comparateur (pour u2) et d'une porte OU-exclusif. Un filtre RC pass-bas à la sortie de la porte donne une tension proportionnelle au déphasage. La lecture de cette tension par le convertisseur A/N de l'Aduino devrait permettre de couper la commande du pont lorsque le déphasage est en dessous d'une certaine valeur.
6. Application : chauffage par induction
La bobine du circuit primaire permet de chauffer par induction une plaque en fer, par exemple le fond d'une boîte de conserve. Il suffit d'approcher la plaque à 1 ou 2 mm de la bobine. Avec une tension d'alimentation de 30 V, si la plaque est approchée à environ 1 mm de la bobine, l'alimentation délivre presque 3 A (son courant maximal). La puissance délivrée par l'alimentation est alors de 90 W. Si on considère que le rendement est d'environ 0,6, on peut estimer la puissance de chauffage à 50 W. Une plaque en fer de 1 mm d'épaisseur devient brûlante en quelques secondes. Cette puissance permet de chauffer 10 g d'eau de 100 K en 84 secondes.
La modélisation de ce système est difficile, car il faudrait connaître non seulement la valeur de L1, qui est certainement fortement augmentée en présence de l'induit (la plaque en fer), mais aussi l'auto-inductance et la résistance équivalente de l'induit.
Si l'on veut utiliser ce chauffage par induction pour faire des mesures physiques, il faut déterminer la puissance reçue par l'induit. Or la seule puissance moyenne que l'on peut mesurer est celle reçue par la bobine (puissance P2). La résistance r2 est connue pour la fréquence de travail grace à une étude préalable de la bobine (Bobines avec noyau). Si on mesure le courant i2(t) dans la bobine en parallèle avec la tension u2(t) à ses bornes, en peut en déduire la puissance moyenne P2 reçue par la bobine et la puissance dissipée, ce qui permet par différence d'obtenir la puissance transmise à l'induit.
Une sonde de courant à effet Hall permet d'obtenir l'intensité du courant en fonction du temps en introduisant une résistance négligeable dans le circuit. L'ACS711 est une sonde de courant à effet Hall. Sa version LC est vendue montée sur une plaque avec connecteurs par Microbot. Lorsqu'elle est alimentée en 5 V, la sortie est à 2,50 V pour un courant nul et la sensibilité est de 190 mV pour 1000 mA. La gamme de courants accessibles est +/- 12,5 A. La bande passante est de 100 kHz. La résistance est 1,2 mΩ, ce qui est tout à fait négligeable devant la résistance interne de la bobine (0,15 Ω).
La sonde comporte deux bornes IP+ et IP- pour la connecter avec le circuit. Si le circuit est alimenté par un demi-pont (délivrant pour la même tension d'alimentation 4 fois moins de puissance qu'un pont complet), il est préférable de connecter la sonde du côté de la bobine relié à la masse (low side), bien que la borne IP- n'ait pas à être reliée à la masse. Si le circuit est alimenté par un pont complet, les deux bornes de la bobines sont symétriques et leur potentiel par rapport à la masse peut atteindre 50 V à la fréquence de 70 kHz, mais beaucoup plus si on s'approche de la résonance de tension. La documentation de l'ACS711 précise que la sonde peut être utilisée dans ces conditions jusqu'à une tension de 100 V. Elle convient donc pour notre application mais il faudra contrôler la tension u2(t) pour que sa valeur de crête ne dépasse pas 100 V (par rapport à la masse).