Filtres passe-bas analogiques et numériques
1. Introduction
Les filtres passe-bas sont très utilisés en traitement du signal. On peut citer quelques applications :
- Extraction de la valeur moyenne d'un signal (composante continue).
- Filtrage du bruit.
- Filtre anti-repliement pour la numérisation des signaux.
- Filtre de lissage pour la conversion numérique-analogique.
Ce document présente une étude expérimentale de filtres passe-bas analogiques, un filtre RC et un filtre actif du second ordre. Un filtre numérique RIF est aussi étudié.
Tous les filtres étudiés ont une fréquence de coupure de 1 kHz. On s'intéresse à la transformation d'un signal périodique. Celui-ci est généré par le programme Pure Data syntheseHarmonique.pdf.
L'acquisisition des signaux et leur traitement sont fait avec Python, en utilisant le module d'interface pour Sysam SP5 présenté dans CAN Eurosmart : interface pour Python.
2. Généralités
L'étude d'un filtre se fait en considérant sa réponse fréquentielle, constituée du gain G(f) et du déphadage ϕ(f), définis pour un signal sinusoïdal.
Un filtre passe-bas idéal a un gain de 1 dans la bande passante 0<f<fc, nul dans la bande atténuée f>fc. La fonction gain d'un filtre réel peut prendre différentes formes. Les filtres analogiques que nous allons étudier ont une réponse de type Butterworth, de la forme suivante :
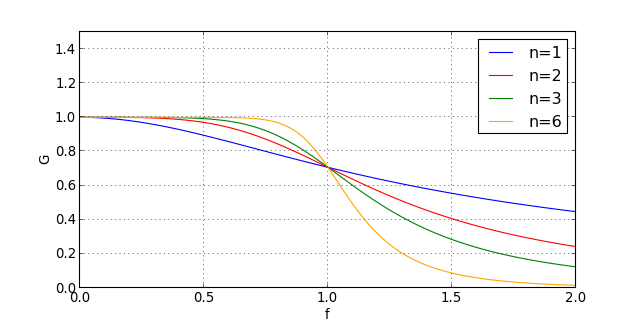
G0 est le gain dans la bande passante. On se place dans le cas G0=1. L'entier n est l'ordre du filtre. Pour voir l'influence de l'ordre du filtre, on trace le gain :
import numpy
import math
from matplotlib.pyplot import *
def G(n,f):
return 1.0/math.sqrt(1+f**(2*n))
n = 500
f = numpy.arange(n)*10.0/n
g1 = numpy.zeros(n)
g2 = numpy.zeros(n)
g3 = numpy.zeros(n)
g6 = numpy.zeros(n)
for k in range(n):
g1[k] = G(1,f[k])
g2[k] = G(2,f[k])
g3[k] = G(3,f[k])
g6[k] = G(6,f[k])
figure(figsize=(8,4))
plot(f,g1,'b',label='n=1')
plot(f,g2,'r',label='n=2')
plot(f,g3,'g',label='n=3')
plot(f,g6,'orange',label='n=6')
xlabel('f')
ylabel('G')
axis([0,2,0,1.5])
legend(loc='upper right')
grid()
 plotA.pdf
plotA.pdf
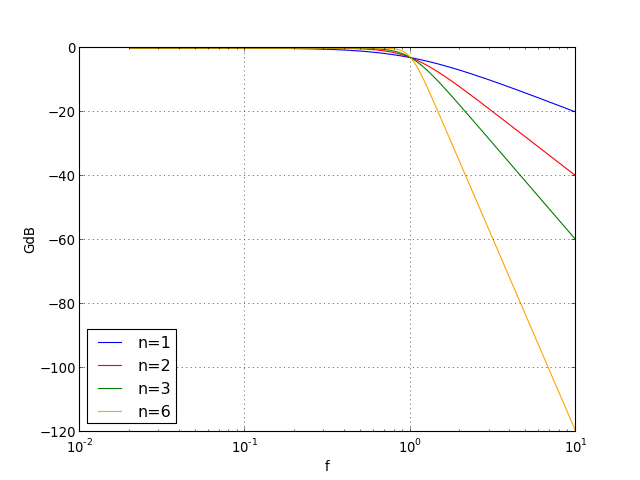
Le gain pour la fréquence de coupure est indépendant de l'ordre (G=0.71). On voit que le gain est loin d'être constant dans la bande passante. Pour obtenir un vraie bande passante, avec un gain constant sur une plage de fréquence assez large, il faut augmenter l'ordre du filtre. Si on s'intéresse à la variation du gain dans la bande atténuée, une courbe logarithmique est plus adaptée (diagramme de Bode) :
gdb1 = 20*numpy.log10(g1)
gdb2 = 20*numpy.log10(g2)
gdb3 = 20*numpy.log10(g3)
gdb6 = 20*numpy.log10(g6)
figure(figsize=(8,6))
plot(f,gdb1,'b',label='n=1')
plot(f,gdb2,'r',label='n=2')
plot(f,gdb3,'g',label='n=3')
plot(f,gdb6,'orange',label='n=6')
xlabel('f')
ylabel('GdB')
xscale('log')
legend(loc='lower left')
grid()
 plotB.pdf
plotB.pdf
Dans la bande atténuée, le filtre d'ordre n présente une pente de -20n décibels par décade. Pour résumer, plus le filtre est d'ordre élevé plus le gain est constant dans la bande passante et plus le gain décroît rapidement dans la bande atténuée. On dit que la sélectivité du filtre augmente avec l'ordre.
Une autre caractéristique du filtre qu'il doit posséder dans la bande passante est la linéarité du déphasage par rapport à la fréquence :
où τ est une constante ayant les dimensions d'un temps. Nous avons placé un signe négatif car la constante de proportionnalité est souvent négative. Considérons un signal périodique comportant un fondamental et une harmonique, les deux dans la bande passante. Supposons pour simplifier que le gain soit 1 pour ces deux harmoniques. L'entrée du filtre s'écrit :
La sortie est :
On voit donc que la sortie est identique à l'entrée, avec un retard τ. Ainsi la linéarité du déphasage par rapport à la fréquence assure-t-elle une transmission des signaux dans la bande passante sans déformation (mais il faut aussi que le gain soit consant).
Pour prendre l'exemple d'un filtre passe-bas utilisé dans le traitement du son, on cherche à obtenir dans la bande passante un gain constant et une phase linéaire de manière à ne pas introduire de distorsion dans le son.
3. Filtres analogiques
3.a. Filtre du premier ordre
Une cellule RC constitue un filtre passe-bas du premier ordre. Voici le montage :
Figure pleine pageLa source de tension représente la sortie audio de l'ordinateur, avec sa résistance de sortie r=50 Ω. On fait une acquisition à la fois sur le signal non filtré (EA0) et sur le signal filtré (EA1). Les valeurs pour le filtre sont R=6.8+0.39=7.2 kΩ et C=22 nF, ce qui donne une fréquence de coupure de 1.0 kHz.
La fonction de transfert est :
Lorsque le déphasage est
ce qui montre que le filtre retarde les signaux (dans la bande passante) d'une durée τ=RC=0.16 ms.
L'inconvénient de ce filtre est son impédance de sortie élevée. On peut remedier facilement à cela en ajoutant un amplificateur suiveur (de gain unité) en sortie. Dans le cas présent, ce n'est pas gênant car l'impédance d'entrée du convertisseur analogique-numérique est très élevé (1 MΩ).
Voici le programme python qui fait l'acquisition et enregistre les données dans un fichier. Il trace aussi le signal en entrée et en sortie du filtre, et le spectre en entrée et en sortie.
import pycan.main as pycan
from matplotlib.pyplot import *
import numpy
import math
import numpy.fft
import os
os.chdir("C:/Users/fred/Documents/electro/TP/filtresPB")
nom = "signal-1"
can = pycan.Sysam("SP5")
can.config_entrees([0,1],[2.0,2.0])
fe=20000.0
T=1.0
te=1.0/fe
N = int(T/te)
print(N)
can.config_echantillon(te*10**6,N)
can.acquerir()
temps = can.temps()
entrees = can.entrees()
t0=temps[0]
u0=entrees[0]
t1=temps[1]
u1=entrees[1]
numpy.savetxt('%s.txt'%nom,[t0,u0,t1,u1])
te = t0[1]-t0[0]
fe = 1.0/te
N = t0.size
T = t0[N-1]-t0[0]
can.fermer()
figure()
plot(t0,u0,'b')
plot(t1,u1,'r')
xlabel("t (s)")
ylabel("u (V)")
axis([0.1,0.12,-2,2])
grid()
savefig("%s-signal.pdf"%nom)
tfd0=numpy.fft.fft(u0)
a0 = numpy.absolute(tfd0)/N
tfd1 = numpy.fft.fft(u1)
a1 = numpy.absolute(tfd1)/N
f=numpy.arange(N)*1.0/T
figure()
plot(f,a0,'b')
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
title("avant filtrage")
savefig("%s-spectre-A.pdf"%nom)
figure()
plot(f,a1,'r')
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
title("apres filtrage")
savefig("%s-spectre-B.pdf"%nom)
show()
Le signal étudié comporte un fondamental et une harmonique de rang 2. On fait varier sa fréquence de 100 à 1000 Hertz, par pas de 100. La fréquence d'échantillonnage est fixée à fe=20 kHz, ce qui nous place en situation de sur-échantillonnage afin d'obtenir facilement un tracé de la forme d'onde. Le temps d'acquisition est T=1.0 s.
La fonction suivante lit un fichier de données et trace le signal en entrée et en sortie :
import numpy
import math
from matplotlib.pyplot import *
import numpy.fft
import scipy.signal
def traceSignaux(nom):
[t0,u0,t1,u1] = numpy.loadtxt(nom)
figure(figsize=(8,4))
plot(t0,u0,'b',label='entree')
plot(t1,u1,'r',label='sortie')
xlabel('t (s)')
ylabel('u (V)')
axis([0.1,0.12,-1,1])
legend(loc='upper right')
grid()
La fonction suivante trace les spectres entre 0 et 2 kHz :
def traceSpectres(nom):
[t0,u0,t1,u1] = numpy.loadtxt(nom)
N = t0.size
T = t0[N-1]-t0[0]
te = t0[1]-t0[0]
fe = 1.0/te
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
a1 =numpy.absolute(numpy.fft.fft(u1*scipy.signal.get_window("hann",N)))/N
max = a0.max()
f=numpy.arange(N)*1.0/T
subplot(211)
plot(f,a0,'b')
ylabel('A')
axis([0,2000,0,max])
grid()
subplot(212)
plot(f,a1,'b')
xlabel('f (Hz)')
ylabel('A')
axis([0,2000,0,max])
grid()
On commence par un signal de fréquence f=100 Hz :
traceSignaux("signal-11.txt")
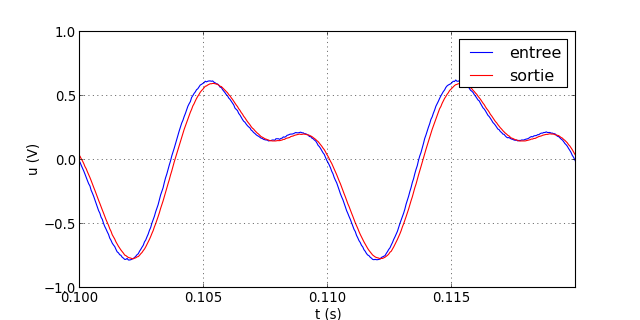 figA.pdf
figA.pdf
traceSpectres("signal-11.txt")
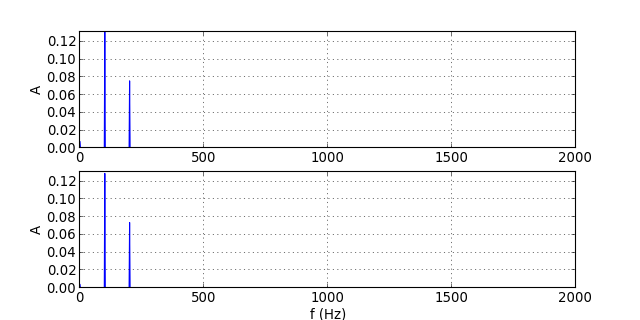 figB.pdf
figB.pdf
Les deux harmoniques sont dans la bande passante. Il n'y a pratiquement pas de déformation du signal, qui présente en sortie le retard τ=RC.
Voici le résultat pour f=300 Hz
traceSignaux("signal-13.txt")
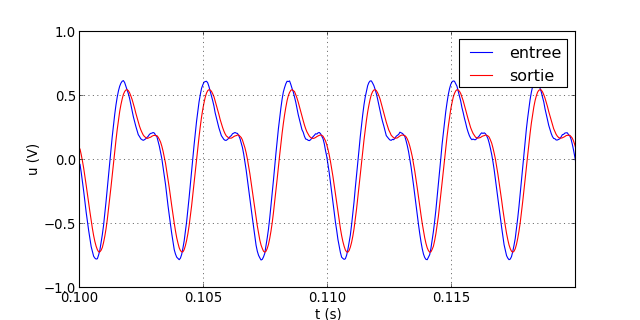 figC.pdf
figC.pdf
traceSpectres("signal-13.txt")
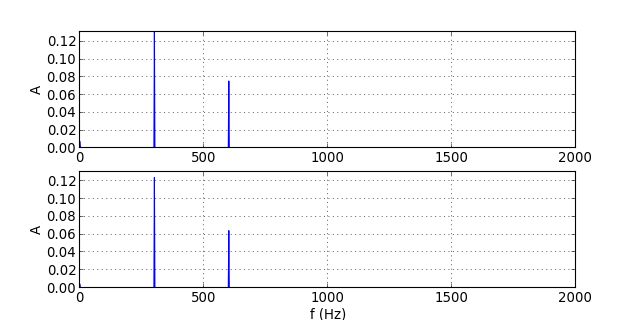 figD.pdf
figD.pdf
Bien que les deux harmoniques soient dans la bande passante, on commence à voir une légère déformation du signal, due au fait que l'harmonique de rang 2 est abaissée en sortie.
Voici le résultat pour f=400 Hz
traceSignaux("signal-14.txt")
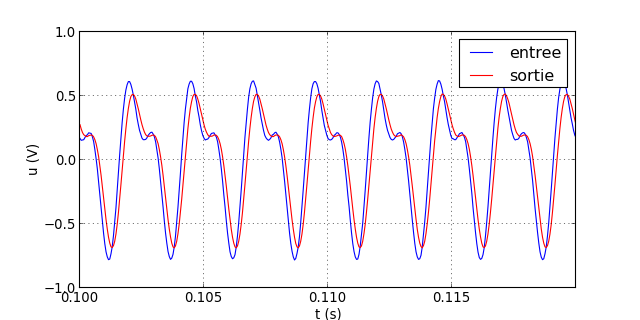 figE.pdf
figE.pdf
traceSpectres("signal-14.txt")
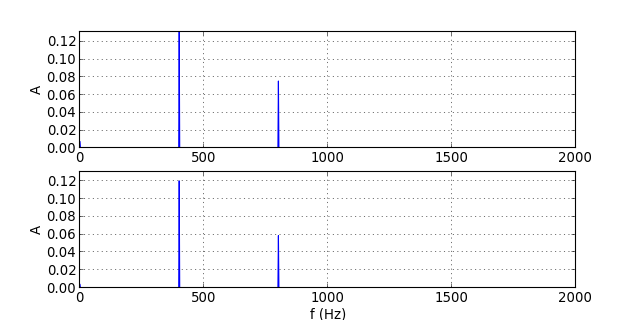 figF.pdf
figF.pdf
La déformation est plus marquée.
Voici le résultat pour f=600 Hz
traceSignaux("signal-16.txt")
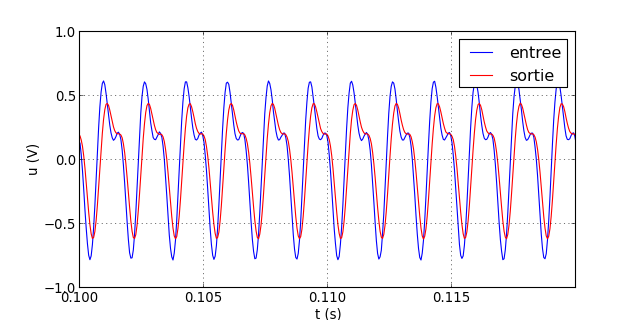 figG.pdf
figG.pdf
traceSpectres("signal-16.txt")
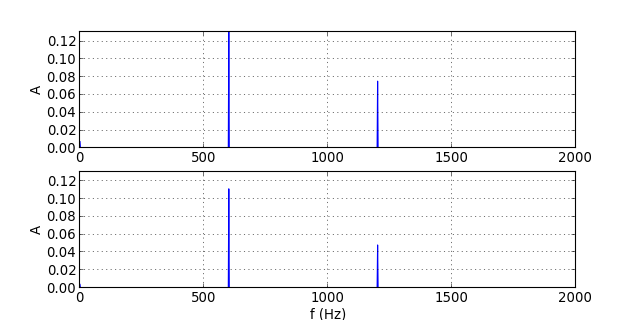 figH.pdf
figH.pdf
Voici le résultat pour f=900 Hz
traceSignaux("signal-19.txt")
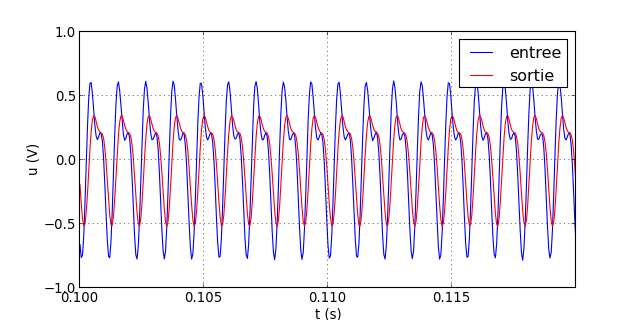 figI.pdf
figI.pdf
traceSpectres("signal-19.txt")
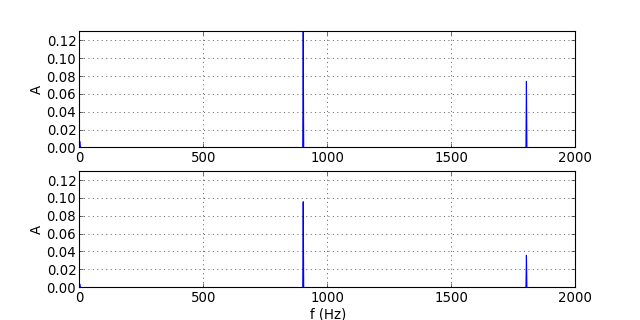 figJ.pdf
figJ.pdf
La déformation est très importante car l'harmonique de rang 2 se trouve dans la bande atténuée. On voit aussi qu'un fitre d'ordre 1 n'est pas assez sélectif pour supprimer l'harmonique de rang 2.
3.b. Filtre d'ordre 2
Dans le montage suivant, un filtre actif de Sallen et Key est utilisé:
Figure pleine pageL'élément actif est un amplificateur suiveur. L'impédance de sortie du filtre est celle de l'amplificateur, ce qui lui donne une valeur assez faible, de l'ordre de quelques Ohms.
Avec R=11.2 kΩ et C=10 nF, la fréquence de coupure est :
Le gain a en principe la forme suivante :
Voici les résultats pour les mêmes fréquences que précédemment :
traceSignaux("signal-1.txt")
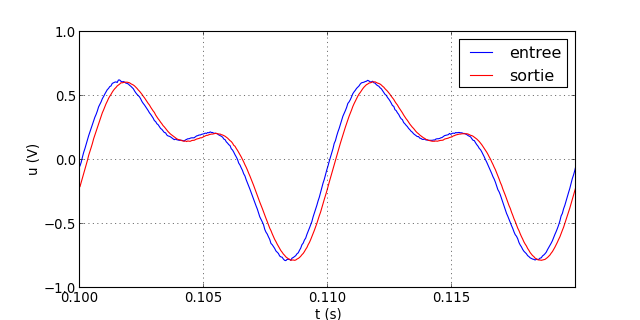 figK.pdf
figK.pdf
traceSpectres("signal-1.txt")
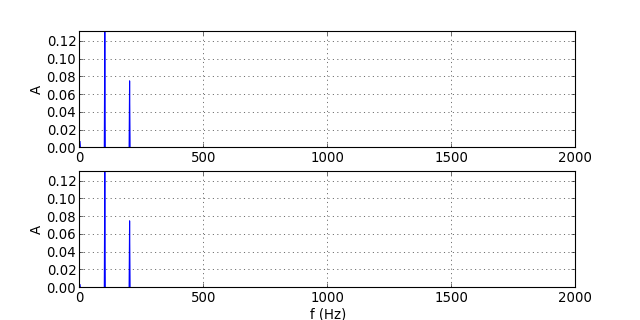 figL.pdf
figL.pdf
traceSignaux("signal-3.txt")
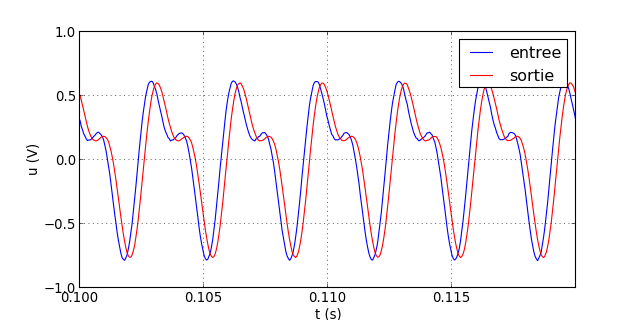 figM.pdf
figM.pdf
traceSpectres("signal-3.txt")
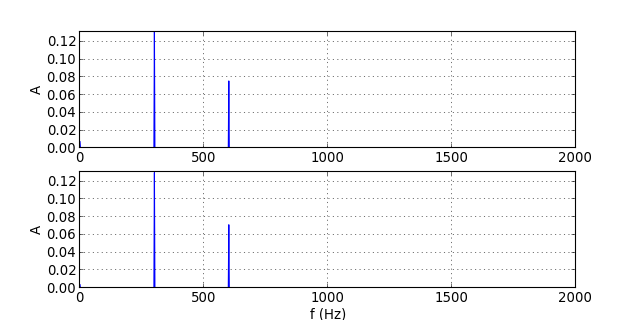 figN.pdf
figN.pdf
traceSignaux("signal-4.txt")
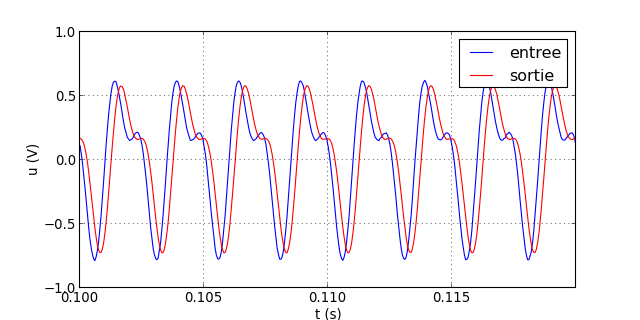 figO.pdf
figO.pdf
traceSpectres("signal-4.txt")
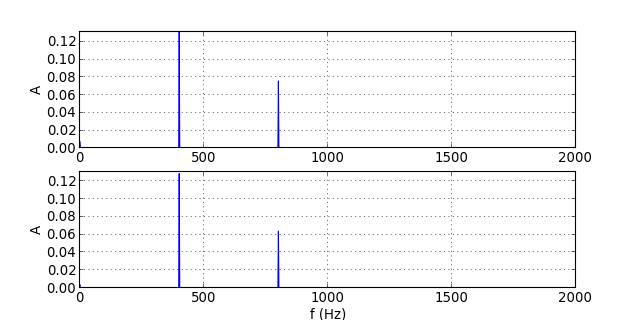 figP.pdf
figP.pdf
traceSignaux("signal-6.txt")
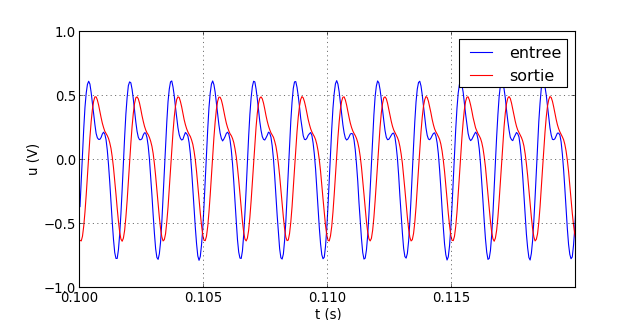 figQ.pdf
figQ.pdf
traceSpectres("signal-6.txt")
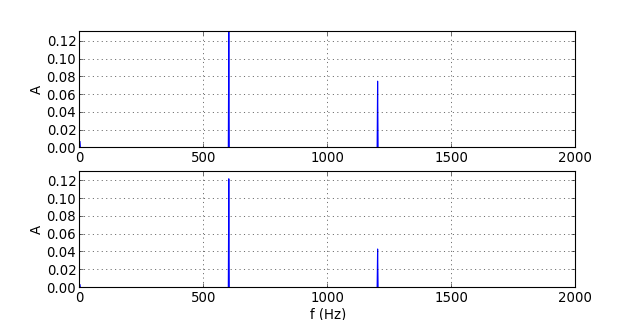 figR.pdf
figR.pdf
traceSignaux("signal-9.txt")
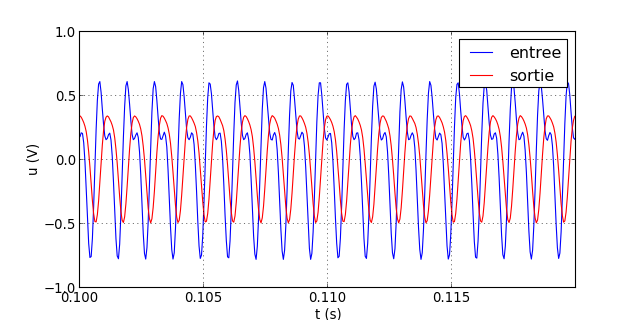 figS.pdf
figS.pdf
traceSpectres("signal-9.txt")
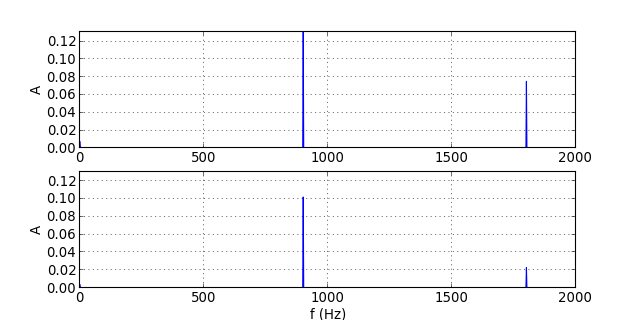 figT.pdf
figT.pdf
Comparé au filtre d'ordre 1, la déformation du signal dans la bande passante se produit à une fréquence un peu plus élevée, mais la différence est en pratique peu marquée. En revanche, l'effet de réduction de l'harmonique de rang 2 lorsqu'elle est dans la bande atténuée est nettement plus important.
4. Filtre numérique
Nous allons utiliser un filtre à réponse impulsionnelle finie (RIF), comme expliqué dans le document Exemples de filtres RIF.
Pour définir ce type de filtre, il faut tout d'abord calculer le rapport de la fréquence de coupure sur la fréquence d'échantillonnage :
Le filtre passe-bas idéal doit avoir un gain de 1 dans la bande passante et 0 dans la bande atténuée. Par ailleurs, le déphasage doit varier linéairement avec la fréquence dans la bande passante, pour que le retard soit indépendant de la fréquence. La réponse impulsionnelle d'un tel filtre est donnée par la fonction suivante :
où la fonction sinus cardinale est définie par :
Pour obtenir une réponse impulsionnelle finie, il faut la tronquer à un rang P, c'est-à-dire garder seulement les indices . Voici le calcul de la réponse impulsionnelle pour P=150.
import math
P=150
h = numpy.zeros(2*P+1)
def sinc(u):
if u==0:
return 1.0
else:
return math.sin(math.pi*u)/(math.pi*u)
a=1.0/20
for k in range(2*P+1):
h[k] = 2*a*sinc(2*(k-P)*a)
indices = numpy.arange(2*P+1)
figure(figsize=(8,4))
vlines(indices,[0],h)
grid()
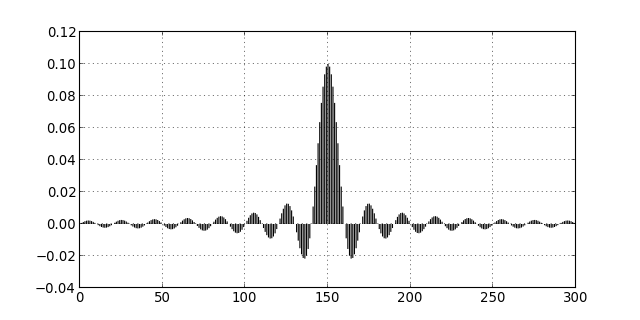 figU.pdf
figU.pdf
Avant d'appliquer ce filtre, il faut étudier sa réponse fréquentielle, c'est-à-dire son gain et son déphasage en fonction de la fréquence. La méthode pour le faire est expliquée dans Introduction aux filtres numériques. Voici la fonction qui permet de le faire :
def reponseFreq(h):
N = h.size
def Hf(f):
s = 0.0
for k in range(N):
s += h[k]*numpy.exp(-1j*2*math.pi*k*f)
return s
f = numpy.arange(start=0.0,stop=0.5,step=0.0001)
hf = Hf(f)
g = numpy.absolute(hf)
phi = numpy.unwrap(numpy.angle(hf))
return [f,g,phi]
Remarque : la fonction scipy.signal.freqz fournit la réponse fréquentielle d'un filtre donné sous forme de fonction de transfert en Z.
Voici donc la réponse fréquentielle du filtre :
(f,g,phi)=reponseFreq(h)
fe = 20000
figure(figsize=(6,4))
plot(f*fe,g)
xlabel('f (Hz)')
ylabel('|H|')
axis([0,2000,0,2])
grid()
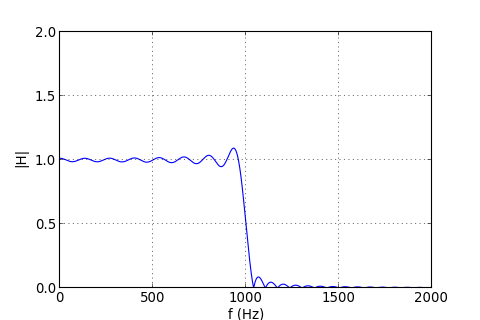 figV.pdf
figV.pdf
On est bien sûr assez loin du filtre idéal, parce-que la réponse impulsionnelle a été tronquée au rang P. Le plus gênant est la présence d'ondulations dans la bande passante. Pour les réduire, on utilise un fenêtrage progressif de la réponse impulsionnelle, par exemple un fenêtrage de Hamming :
import scipy.signal
h = h*scipy.signal.get_window("hamming",2*P+1)
(f,g,phi)=reponseFreq(h)
figure(figsize=(6,4))
plot(f*fe,g)
xlabel('f (Hz)')
ylabel('|H|')
axis([0,2000,0,2])
grid()
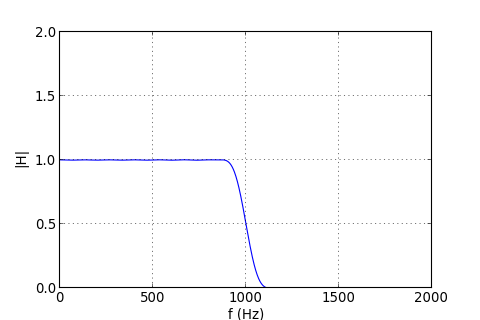 figW.pdf
figW.pdf
Il n'y a plus d'ondulations. On remarque que le gain à la coupure est 1/2. Si l'on veut retrouver la définition de la coupure utilisée en filtrage analogique, il faut abaisser légèrement le paramètre a.
Pour voir ce qu'il se passe dans la bande atténuée, on trace aussi le diagramme de Bode.
figure(figsize=(6,5))
plot(f*fe,20*numpy.log10(g))
xlabel('f (Hz)')
ylabel('GdB')
xscale('log')
grid()
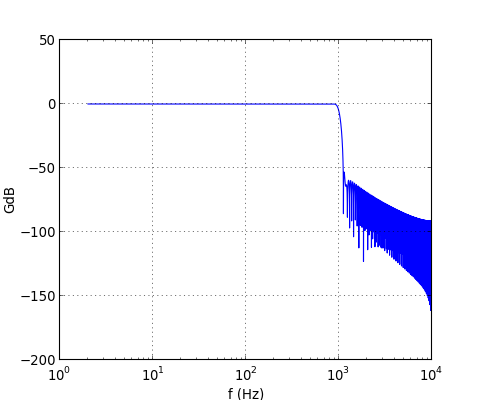 figW1.pdf
figW1.pdf
On constate que la chute du gain est très rapide, de -50 décibels sur quelques Hertz. Cela est dû à la grande valeur choisie pour P. On obtient ainsi un filtre très sélectif, sans commune mesure avec ce qu'il est possible d'obtenir en filtrage analogique.
Pour filtrer les échantillons, il faut effectuer une convolution avec la réponse impulsionnelle. La fonction scipy.signal.convolve permet de le faire. L'option mode='valid' permet de calculer la convolution seulement pour les points valides, c'est-à-dire à partir du point d'indice 2P.
La fonction suivante récupère le signal d'entrée d'un fichier de données pour le filtrer et trace le signal d'entrée et le signal filtré. Le signal filtré comporte moins de points que le signal de départ (2P+1 en moins). Il faut donc recalculer l'échelle de temps. Pour simuler l'effet d'un filtre numérique temps-réel, on attribue l'instant (2P+1)te au premier points calculé en sortie. Cela signifie que le retard de la sortie sur l'entrée est τ=Pte.
def filtrageNum(nom,P,h):
[t0,u0,t1,u1] = numpy.loadtxt(nom)
u2 = scipy.signal.convolve(u0,h,mode='valid')
te = t0[1]-t0[0]
t2 = numpy.arange(2*P+1,2*P+1+u2.size)*te
figure(figsize=(8,4))
plot(t0,u0,'b',label='entree')
plot(t2,u2,'r',label='sortie')
xlabel('t (s)')
ylabel('u (V)')
axis([0.1,0.12,-1,1])
legend(loc='upper right')
grid()
Voici le résultat du filtrage pour le signal de fréquence 300 Hz :
filtrageNum("signal-3.txt",P,h)
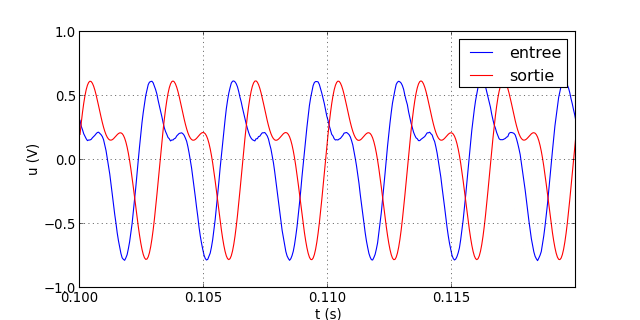 figX.pdf
figX.pdf
La sortie est identique à l'entrée, ce qui est logique car les deux harmoniques sont dans la bande passante, où le gain est égal à 1. Le décalage entre les deux est τ=Pte=5 ms. Le retard est plus grand que pour les filtres analogiques, mais celui-ci est proportionnel à P. Dans le cas présent, si P est supérieur à 100, le retard dépasse une période.
Voyons le résultat à 400 Hz :
filtrageNum("signal-4.txt",P,h)
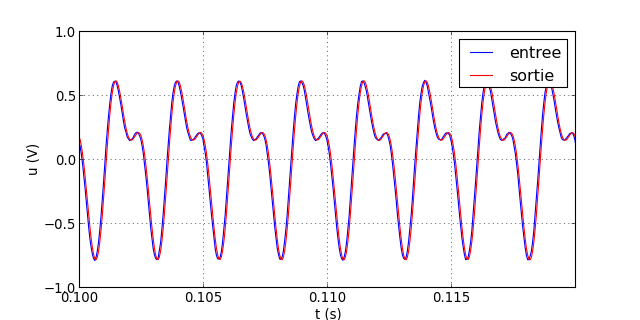 figY.pdf
figY.pdf
Les deux harmoniques sont toujours dans la bande passante. Le retard est multiple d'une période donc les deux signaux coïncident.
Voyons le résultat à 500 Hz :
filtrageNum("signal-5.txt",P,h)
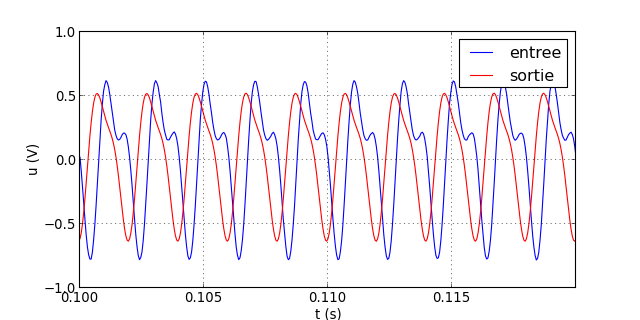 figZ.pdf
figZ.pdf
À cette fréquence, l'harmonique de rang 2 se trouve juste à la fréquence de coupure, avec un gain de 0.5, alors que le fondamental a toujours un gain de 1. Cela donne bien sûr une déformation importante en sortie. Voyons le résultat à 600 Hz :
filtrageNum("signal-6.txt",P,h)
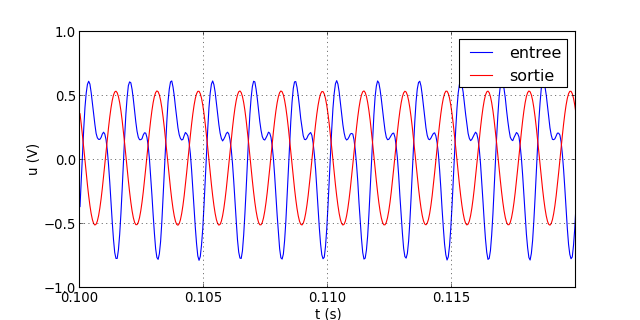 figZA.pdf
figZA.pdf
L'harmonique de rang 2 se trouve dans la bande atténuée, avec un gain pratiquement nul (de l'ordre de -50 décibel). On obtient donc en sortie le fondamental. On voit ainsi la sélectivité très forte de ce filtre, capable d'isoler le fondamental de l'harmonique de rang 2, ce qu'un filtre analogique ne peut faire.
5. Conclusion
Le filtre passe-bas numérique permet d'obtenir une sélectivité très forte, pratiquement impossible à obtenir avec un filtre analogique. Cette grande sélectivité s'obtient avec une valeur importante de l'indice de troncature P. Pour obtenir chaque point en sortie, le produit de convolution nécessite le calcul de 2P+1 termes à sommer. Cela ne pose pas de problème, car il existe aujourd'hui des processeurs de signaux (Digital Signal Processor ou DSP) capables de calculer de telles convolutions à des cadences de plusieurs mégahertz, voire gigahertz pour les dernières générations.
L'autre avantage des filtres numériques est leur grande souplesse de réglage. Il suffit de recalculer la réponse impulsionnelle pour modifier la fréquence de coupure ou l'ordre du filtre, ce qui prend quelques microsecondes.
La supériorité des filtres numériques est telle qu'il devient aujourd'hui courant d'utiliser des processeurs (DSP) effectuant la numérisation, le filtrage et la reconversion en analogique.
Il y a bien sûr des situations où les filtres analogiques sont irremplaçables, par exemple à l'interface entre les circuits analogiques et numériques (filtres anti-repliement et filtres de reconstruction).