Filtres anti-repliement
1. Introduction
La numérisation des signaux doit respecter le critère de Nyquist-Shannon, expliqué dans le document Échantillonnage et reconstruction d'un signal périodique : la fréquence d'échantillonnage fe doit être supérieure au double de la plus grande fréquence présente dans le spectre du signal 2fmax. Lorsque cette condition n'est pas respectée, on est en situation de sous-échantillonnage et il peut se produire un repliement de spectre, qui conduit à l'apparition de fréquences dans le signal.
Le sous-échantillonnage peut se produire dans les deux cas suivants :
- Le convertisseur analogique-numérique (CAN) n'est pas assez rapide pour assurer la condition de Nyquist-Shannon.
- Le convertisseur est assez rapide mais on souhaite stocker ou transmettre l'information à une cadence inférieure à 2fmax.
Dans le premier cas, le seul remède est l'utilisation d'un filtre anti-repliement analogique qui traite le signal avant sa numérisation. Aujourd'hui, il est rare que cette situation se produise car les CAN rapides (de l'ordre du MHz et plus) sont disponibles à faible coût. Par exemple, pour la numérisation du son, le sur-échantillonnage se fait couramment.
Le deuxième cas se produit plus fréquemment, car le stockage et le transfert de l'information doit se faire avec le minimum de données permettant de restituer correctement le signal. Par exemple dans le cas du son Hi-Fi, il est inutile de stocker le signal échantillonné à un fréquence supérieure à 40 kHz car les sons audibles ne vont pas au delà de 20 kHz. Si l'échantillonnage se fait à une fréquence supérieure pour éviter le repliement, par exemple 192 kHz, il faut réduire la fréquence d'échantillonnage avant de stocker les données. Cette réduction ne peut se faire qu'après avoir appliqué un filtre anti-repliement numérique, bien plus facile à réaliser qu'un filtre anti-repliement analogique.
Ce document présente la réalisation de filtres anti-repliement analogiques. Nous verrons aussi la méthode consistant à sur-échantillonner avant d'effectuer un filtrage anti-repliement numérique puis de réduire la fréquence.
On suppose que l'on doit numériser un signal dont la bande de fréquence utile est [0,1] kHz. Ce signal comporte néanmoins des harmoniques en dehors de cette bande (jusqu'au rang 4). On dispose pour cela d'un CAN dont les fréquences d'échantillonnage possibles sont 2 kHz, 5 kHz et 10 kHz.
Le signal est généré par le programme Pure Data syntheseHarmonique.pdf.
L'acquisisition des signaux et leur traitement sont fait avec Python, en utilisant le module d'interface pour Sysam SP5 présenté dans CAN Eurosmart : interface pour Python.
2. Filtres anti-repliement analogiques
2.a. Filtre du premier ordre
La bande utile du signal étant [0,1] kHz, on utilise un filtre passe-bas RC du premier ordre, avec une fréquence de coupure 1 kHz, dans le but de réduire les harmoniques situées en dehors de la bande utile.
Figure pleine pageLa source de tension représente la sortie audio de l'ordinateur, avec sa résistance de sortie r=50 Ω. On fait une acquisition à la fois sur le signal non filtré (EA0) et sur le signal filtré (EA1). Les valeurs pour le filtre sont R=6.8+0.39=7.2 kΩ et C=22 nF, ce qui donne une fréquence de coupure de 1.0 kHz.
Voici le programme python qui fait l'acquisition et enregistre les données dans un fichier. Il trace aussi le signal en entrée du filtre, et le spectre en entrée et en sortie.
import pycan.main as pycan
from matplotlib.pyplot import *
import numpy
import math
import numpy.fft
import os
os.chdir("C:/Users/fred/Documents/electro/TP/antiRepliement")
nom = "signal-1"
can = pycan.Sysam("SP5")
can.config_entrees([0,1],[2.0,2.0])
fe=2000.0
T=10.0
te=1.0/fe
N = int(T/te)
print(N)
can.config_echantillon(te*10**6,N)
can.acquerir()
temps = can.temps()
entrees = can.entrees()
t0=temps[0]
u0=entrees[0]
t1=temps[1]
u1=entrees[1]
numpy.savetxt('%s.txt'%nom,[t0,u0,t1,u1])
te = t0[1]-t0[0]
fe = 1.0/te
N = t0.size
T = t0[N-1]-t0[0]
can.fermer()
figure()
plot(t1,u1,'b')
xlabel("t (s)")
ylabel("u (V)")
axis([0,0.5,-2,2])
grid()
savefig("%s-signal.pdf"%nom)
tfd0=numpy.fft.fft(u0)
a0 = numpy.absolute(tfd0)/N
tfd1 = numpy.fft.fft(u1)
a1 = numpy.absolute(tfd1)/N
f=numpy.arange(N)*1.0/T
figure()
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
title("avant filtrage")
savefig("%s-spectre-A.pdf"%nom)
figure()
plot(f,a1)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
title("apres filtrage")
savefig("%s-spectre-B.pdf"%nom)
show()
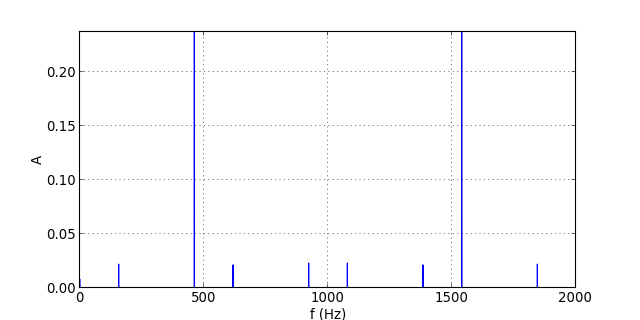
Le signal périodique comporte un fondamental, de fréquence 461 Hz et d'amplitude 1 V, et des harmoniques de rang 2,3 et 4, toutes d'amplitude 0.1.
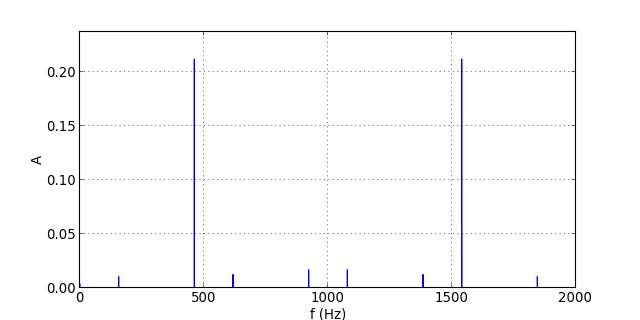
La durée de l'acquisition est toujours T=10.0 s, ce qui fait environ 500 périodes. On commence par la fréquence d'échantillonnage fe=2 kHz. Voici les spectres des signaux échantillonnés en entrée et en sortie du filtre :
import numpy
import scipy.signal
from matplotlib.pyplot import *
[t0,u0,t1,u1] = numpy.loadtxt('signal-1.txt')
N = t0.size
T = t0[N-1]-t0[0]
te = t0[1]-t0[0]
fe = 1.0/te
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
 figA.pdf
figA.pdf
a1 =numpy.absolute(numpy.fft.fft(u1*scipy.signal.get_window("hann",N)))/N
figure(figsize=(8,4))
plot(f,a1)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
 figB.pdf
figB.pdf
Les harmoniques de rang 3 et 4 se replient dans la bande [0,1] kHz, ce qui était prévisible puisque leur fréquence est supérieure à la fréquence de Nyquist (fn=fe/2). Le filtre passe-bas atténue un peu ces harmoniques, ce qui réduit un peu le repliement (ou plutôt ses conséquences) sur le signal de sortie. Néanmoins, l'efficacité du filtre est très faible. En effet, l'harmonique de rang 3 a une fréquence égale à seulement 1.4 fois la fréquence de coupure, ce qui fait une atténuation de seulement -4.6 dB. On en conclue qu'un filtre du premier ordre est insuffisant pour éviter le repliement de bande, du moins à cette fréquence d'échantillonnage.
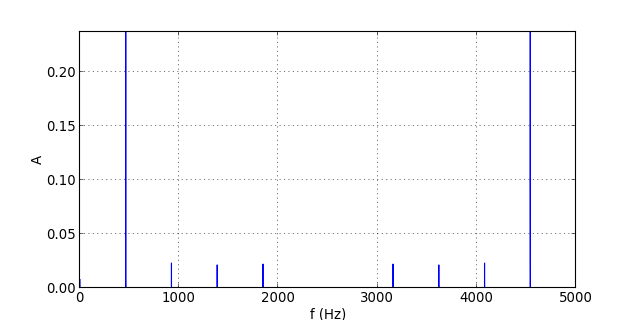
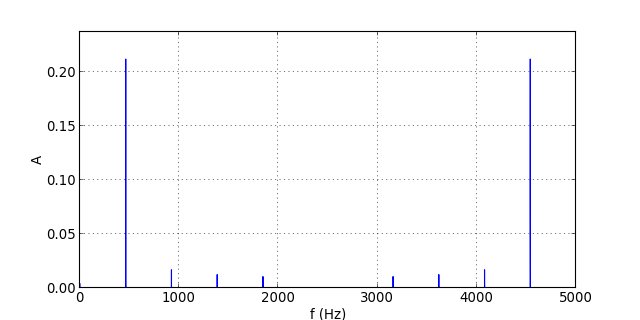
Voyons les spectres à une fréquence fe=5 kHz :
[t0,u0,t1,u1] = numpy.loadtxt('signal-2.txt')
N = t0.size
T = t0[N-1]-t0[0]
te = t0[1]-t0[0]
fe = 1.0/te
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
 figC.pdf
figC.pdf
a1 =numpy.absolute(numpy.fft.fft(u1*scipy.signal.get_window("hann",N)))/N
figure(figsize=(8,4))
plot(f,a1)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
 figD.pdf
figD.pdf
Il n'y a plus de repliement puisque toutes les harmoniques ont une fréquence inférieure à celle de Nyquist.
Pour un signal de plus grande fréquence, il faudra néanmoins encore augmenter la fréquence d'échantillonnage. Voici par exemple un signal de 894 Hz échantillonné à cette fréquence :
[t0,u0,t1,u1] = numpy.loadtxt('signal-4.txt')
N = t0.size
T = t0[N-1]-t0[0]
te = t0[1]-t0[0]
fe = 1.0/te
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
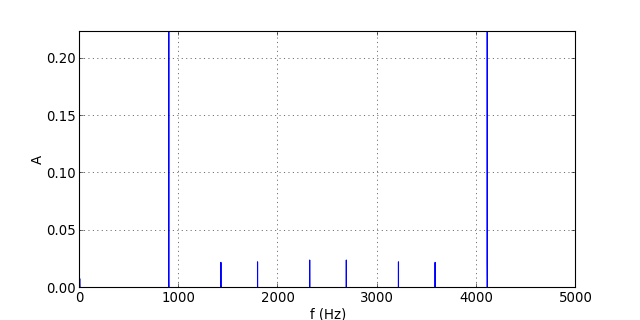 figE.pdf
figE.pdf
a1 =numpy.absolute(numpy.fft.fft(u1*scipy.signal.get_window("hann",N)))/N
figure(figsize=(8,4))
plot(f,a1)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
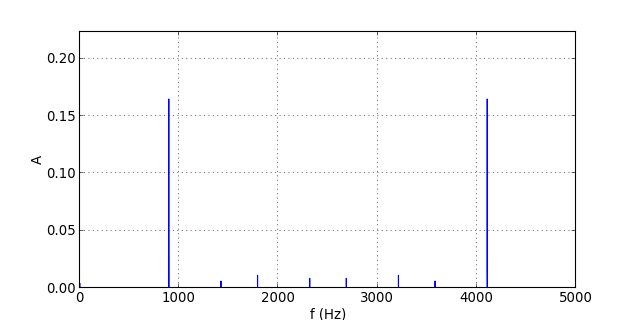 figF.pdf
figF.pdf
Il y a un repliement pour les harmoniques de rang 3 et 4, qui sont quand même bien réduites par le filtre.
2.b. Filtre du second ordre
Compte tenu de l'efficacité très médiocre du filtre RC comme filtre anti-repliement, on est amené à utiliser un filtre d'ordre 2. Dans le montage suivant, un filtre passe-bas de Sallen et Key est utilisé:
Figure pleine pageAvec R=10+1.2=11.2 kΩ et C=10 nF, la fréquence de coupure est :
Le gain a en principe la forme suivante :
On reprend l'exemple du signal de fréquence 461 Hz déjà vu ci-dessus. Voici les spectres en entrée et en sortie du filtre pour une fréquence d'échantillonnage fe=2 kHz :
[t0,u0,t1,u1] = numpy.loadtxt('signal-6.txt')
N = t0.size
T = t0[N-1]-t0[0]
te = t0[1]-t0[0]
fe = 1.0/te
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
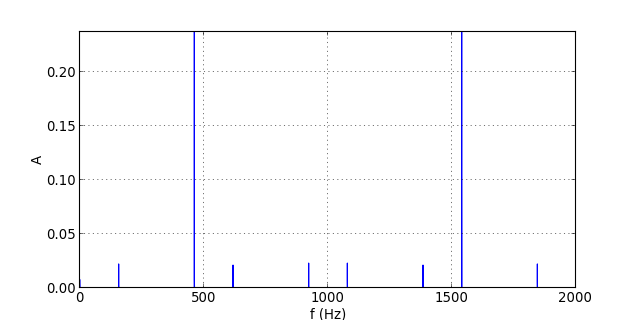 figG.pdf
figG.pdf
a1 =numpy.absolute(numpy.fft.fft(u1*scipy.signal.get_window("hann",N)))/N
figure(figsize=(8,4))
plot(f,a1)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
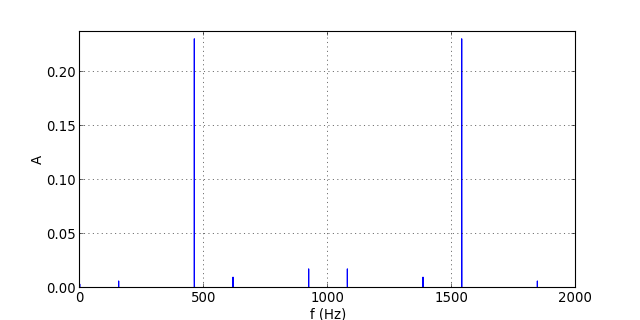 figH.pdf
figH.pdf
Le repliement affecte les harmoniques de rang 3 et 4. Le filtre permet de les atténuer. L'efficacité est bien meilleure qu'avec le filtre du premier ordre. Pour l'harmonique de rang 3, le gain est ici de -6.8 dB, contre -4.6 dB pour le filtre du premier ordre (le gain pour le fondamental est à peu près le même).
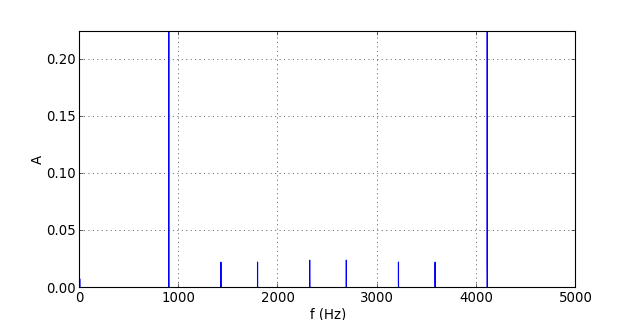
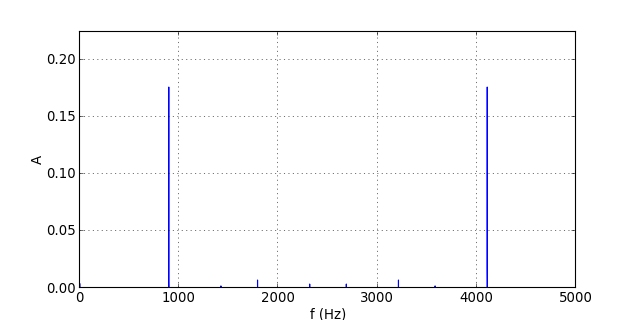
Voyons le résultat pour le signal à 894 Hz échantillonné à 5 kHz :
[t0,u0,t1,u1] = numpy.loadtxt('signal-10.txt')
N = t0.size
T = t0[N-1]-t0[0]
te = t0[1]-t0[0]
fe = 1.0/te
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
 figI.pdf
figI.pdf
a1 =numpy.absolute(numpy.fft.fft(u1*scipy.signal.get_window("hann",N)))/N
figure(figsize=(8,4))
plot(f,a1)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
 figJ.pdf
figJ.pdf
Le repliement affecte les harmoniques 3 et 4, mais elles sont bien atténuées par le filtre.
On déduit de ces résultats que le filtre d'ordre 2 est bien le minimum pour effectuer un anti-repliement efficace. Le résultat n'est toutefois pas parfait, mais peut être amélioré en associant des filtres en série pour obtenir un filtre d'ordre plus élevé, comme expliqué dans le document Filtres actifs de Sallen et Key.
Pour conclure, un filtre analogique anti-repliement efficace est relativement difficile à réaliser, c'est pourquoi cette méthode doit être réservée aux cas où il n'est pas possible d'augmenter la fréquence d'échantillonnage.
3. Filtre anti-repliement numérique
3.a. Principe
Lorsque cela est possible, le sur-échantillonnage doit être privilégié. Nous allons donc utiliser les échantillons prélevés à la fréquence maximale de 10 kHz. Comme le signal utile que l'on souhaite conserver se trouve dans la bande [0,1] kHz, nous devons réduire la fréquence d'échantillonnage d'un facteur 5 avant de stocker les données ou de les transmettre. Un exemple d'application de cette méthode est la numérisation du son, dans laquelle l'échantillonnage se fait à 172 kHz et le stockage à 44 kHz, soit une réduction d'un facteur 4. Pour faire cette réduction, il ne suffit pas de garder un échantillon sur 5, car cela ferait réapparaitre le repliement de bande. Il faut tout d'abord effectuer un filtrage passe-bas des échantillons, avec une fréquence de coupure de 1 kHz. Il s'agit en fait d'un filtre anti-repliement numérique.
3.b. Calcul du filtre
Une manière simple d'effectuer ce filtrage serait de prendre la valeur moyenne de 5 échantillons successifs pour obtenir un échantillon.
Pour obtenir un meilleur résultat, nous allons utiliser un filtre à réponse impulsionnelle finie (RIF), comme expliqué dans le document Exemples de filtres RIF.
Pour définir ce type de filtre, il faut tout d'abord calculer le rapport de la fréquence de coupure sur la fréquence d'échantillonnage :
Le filtre passe-bas idéal doit avoir un gain de 1 dans la bande passante et 0 dans la bande atténuée. Par ailleurs, le déphasage doit varier linéairement avec la fréquence dans la bande passante, pour que le retard soit indépendant de la fréquence. La réponse impulsionnelle d'un tel filtre est donnée par la fonction suivante :
où la fonction sinus cardinale est définie par :
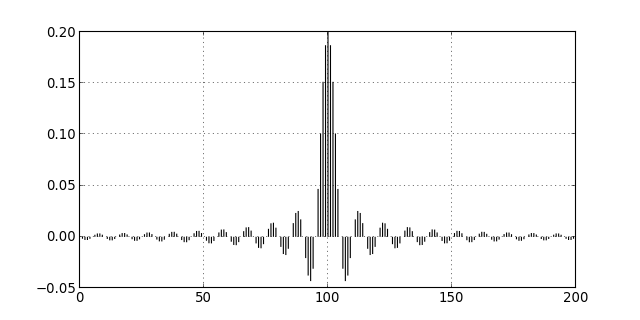
Pour obtenir une réponse impulsionnelle finie, il faut la tronquer à un rang P, c'est-à-dire garder seulement les indices . Voici le calcul de la réponse impulsionnelle pour P=100.
import math
P=100
h = numpy.zeros(2*P+1)
def sinc(u):
if u==0:
return 1.0
else:
return math.sin(math.pi*u)/(math.pi*u)
a=0.10
for k in range(2*P+1):
h[k] = 2*a*sinc(2*(k-P)*a)
indices = numpy.arange(2*P+1)
figure(figsize=(8,4))
vlines(indices,[0],h)
grid()
 figK.pdf
figK.pdf
Avant d'appliquer ce filtre, il faut étudier sa réponse fréquentielle, c'est-à-dire son gain et son déphasage en fonction de la fréquence. La méthode pour le faire est expliquée dans Introduction aux filtres numériques. Voici la fonction qui permet de le faire :
def reponseFreq(h):
N = h.size
def Hf(f):
s = 0.0
for k in range(N):
s += h[k]*numpy.exp(-1j*2*math.pi*k*f)
return s
f = numpy.arange(start=0.0,stop=0.5,step=0.0001)
hf = Hf(f)
g = numpy.absolute(hf)
phi = numpy.unwrap(numpy.angle(hf))
return [f,g,phi]
Remarque : la fonction scipy.signal.freqz fournit la réponse fréquentielle d'un filtre donné sous forme de fonction de transfert en Z.
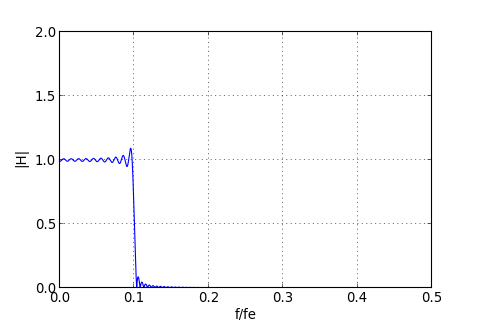
Voici donc la réponse fréquentielle du filtre :
(f,g,phi)=reponseFreq(h)
figure(figsize=(6,4))
plot(f,g)
xlabel('f/fe')
ylabel('|H|')
axis([0,0.5,0,2])
grid()
 figL.pdf
figL.pdf
On est bien sûr assez loin du filtre idéal, parce-que la réponse impulsionnelle a été tronquée au rang P. Le plus gênant est la présence d'ondulations dans la bande passante. Pour les réduire, on utilise un fenêtrage progressif de la réponse impulsionnelle, par exemple un fenêtrage de Hamming :
import scipy.signal
h = h*scipy.signal.get_window("hamming",2*P+1)
(f,g,phi)=reponseFreq(h)
figure(figsize=(6,4))
plot(f,g)
xlabel('f/fe')
ylabel('|H|')
axis([0,0.5,0,2])
grid()
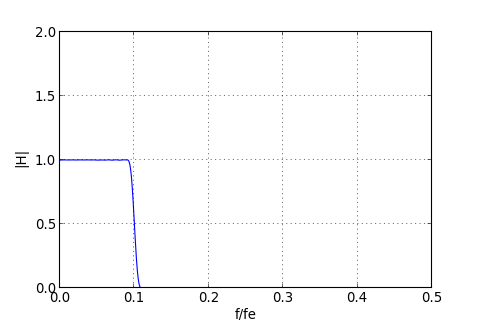 figM.pdf
figM.pdf
Il n'y a plus d'ondulations. La sélectivité semble suffisante pour notre usage. On remarque que le gain à la coupure est 1/2.
Pour filtrer les échantillons, il faut effectuer une convolution avec la réponse impulsionnelle. Nous allons le faire sur les échantillons du signal de 461 Hz échantillonné à 10 Hz
[t0,u0,t1,u1] = numpy.loadtxt('signal-8.txt')
u3 = scipy.signal.convolve(u0,h)
On commence par comparer le signal et le signal filtré dans le domaine temporel :
figure(figsize=(8,4))
plot(u0[1000:1100],'b')
plot(u3[1000:1100],'r')
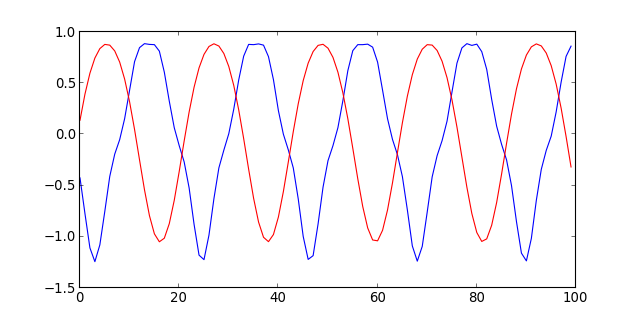 figN.pdf
figN.pdf
Ce graphique n'apporte pas beaucoup d'informations, même si l'on devine que des harmoniques ont été supprimées. Il vaut mieux faire la comparaison dans le domaine fréquentiel, c'est-à-dire sur les spectres :
te = t0[1]-t0[0]
fe = 1.0/te
N = u0.size
T = te*N
a0 =numpy.absolute(numpy.fft.fft(u0*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a0)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
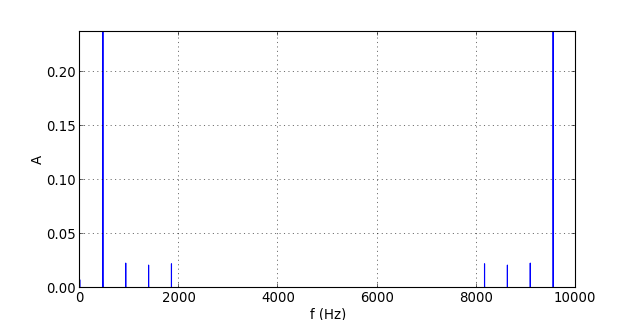 figO.pdf
figO.pdf
te = t0[1]-t0[0]
fe = 1.0/te
N = u3.size
T = te*N
a3 =numpy.absolute(numpy.fft.fft(u3*scipy.signal.get_window("hann",N)))/N
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a3)
xlabel("f (Hz)")
ylabel("A")
axis([0,fe,0,a0.max()])
grid()
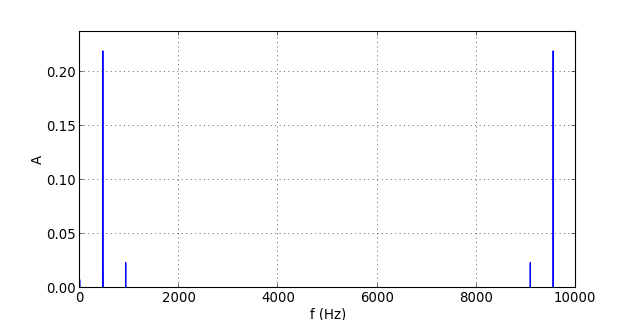 figP.pdf
figP.pdf
Les harmoniques au dessus de 1 kHz ont bien été supprimées. On peut à présent réduire la fréquence d'échantillonnage à 2 kHz, en gardant un échantillon sur 5.
u4 = numpy.zeros(0)
i = 0
while i<u3.size:
u4 = numpy.append(u4,u3[i])
i += 5
Pour vérifier, on calcule le spectre de ces nouveaux échantillons :
N = u4.size
a4 =numpy.absolute(numpy.fft.fft(u4*scipy.signal.get_window("hann",N)))/N
T = N*te*5
f=numpy.arange(N)*1.0/T
figure(figsize=(8,4))
plot(f,a4)
xlabel("f (Hz)")
ylabel("A")
grid()
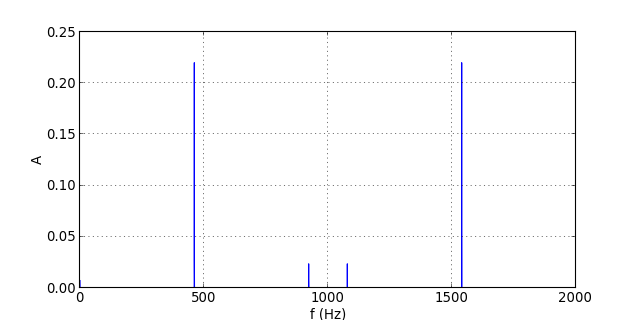 figQ.pdf
figQ.pdf
Le résultat est excellent : les harmoniques de rang 3 et 4, qui auraient donné un repliement à cette fréquence, ont complètement disparu.
Pour finir, voyons quel serait l'ordre d'un filtre analogique (de type Butterworth) qui donnerait la même réponse fréquentielle que le filtre numérique ci-dessus :
n=50
def G(f):
return 1.0/math.sqrt(1+(f/0.1)**(2*n))
f = numpy.arange(500)*1.0/500
g = numpy.zeros(f.size)
for k in range(f.size):
g[k] = G(f[k])
figure(figsize=(6,4))
plot(f,g)
xlabel("f/fe")
ylabel("G")
axis([0,0.5,0,2])
grid()
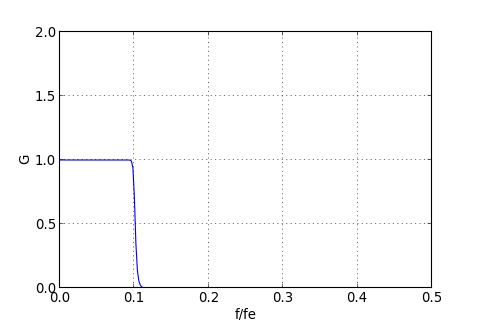 figR.pdf
figR.pdf
Pour obtenir ce filtre, il faudrait associer 25 cellules de type Sallen et Key. Autant dire qu'un tel filtre est irréalisable dans le domaine analogique.