Modèle filaire du rotor et du stator d'un moteur synchrone

1. Introduction

Ce document présente un modèle de stator et de rotor pour un moteur synchrone, ou plus généralement une machine synchrone. Les bobinages (ou les aimants du rotor) sont supposés très longs dans la direction de l'axe (Oz) de la machine. Les éléments du rotor et du stator sont donc assimilés à des fils rectilignes (infini) de direction (Oz). Ce modèle ne prend pas en compte la présence des parties en fer. L'objectif est de déterminer le couple exercé par le stator sur le rotor et le flux magnétique généré par le rotor dans le stator, qui permettra de calculer la force électromotrice générée dans le stator par le mouvement du rotor. Cette force électromotrice est intéressante dans le cas d'une génératrice puisqu'il s'agit de la tension à vide aux bornes du stator. Dans le cas d'un moteur, cette f.é.m. est la force contre-électromotrice, qu'il faut prendre en compte pour modéliser le comportement électrique du stator. Dans ce document, on s'intéresse principalement au cas d'un moteur, pour lequel le courant dans le stator est imposé.

2. Système élémentaire

L'espace est muni d'un repère (Oxyz) où (Oz) est l'axe du moteur. On considère un stator de rayon a_s et plus particulièrement une spire du bobinage du stator, de forme rectangulaire. Sa longueur $ℓ$ est supposée très grande par rapport à sa largeur, ce qui permet de modéliser la spire par deux fils rectilignes infinis parallèles, comme indiqué sur la figure suivante. Ces deux fils sont disposés sur le cercle de rayon a_s. L'axe de cette spire (la médiatrice des deux fils) fait un angle $θ_{s}$ par rapport à (Ox) et la distance angulaire par rapport au centre O entre les deux fils est $2 α_{s}$ . L'intensité du courant électrique dans la spire est notée i_s(t). Une spire du rotor (ou un aimant) est représentée de manière similaire. On considère donc deux fils rectilignes infinis situés à une distance a_r de l'axe, faisant entre elles un angle $2 α_{r}$ par rapport au point O et dont la médiatrice fait un angle $θ_{r}$ par rapport à l'axe (Ox).

Figure pleine page

Dans chaque fil, la convention de sens pour l'intensité algébrique du courant est indiquée sur la figure. Si cette intensité est positive, le champ magnétique généré par la spire est dans le sens radial sortant. Pour la modélisation d'un moteur complet, toutes les spires devront respecter cette convention.

On nommera bobine la partie du bobinage du stator (ou du rotor) qui peut être représentée par une spire de ce modèle.

Les intersections des fils rectilignes avec le plan (oxy) sont notées P_r,Q_r,P_s,Q_s. Les coordonnées de ces points s'expriment sans difficulté en fonction des rayons a_s,a_r et des angles $θ_{s}, α_{s}, θ_{r}, α_{r}$ .

Le champ magnétique créé par un fil situé au point P et parcouru par un courant d'intensité i(t) (compté dans le sens de ${\vec{u}}_{z}$ ) s'écrit :

\vec{B} (M, t) = \frac{μ_{0} i (t)}{2 π {(P M)}^{2}} ({\vec{u}}_{z} \land \vec{P M}) (1)

où PM désigne la distance entre P et M. Le champ créé par la bobine du stator en un point M s'écrit donc :

{\vec{B}}_{s} (M, t) = \frac{μ_{0} i_{s} (t)}{2 π} (\frac{{\vec{u}}_{z} \land \vec{P_{s} M}}{P_{s} M^{2}} - \frac{{\vec{u}}_{z} \land \vec{Q_{s} M}}{Q_{s} M^{2}}) (2)

De même, le champ créé par la bobine du rotor s'écrit :

{\vec{B}}_{r} (M, t) = \frac{μ_{0} i_{r}}{2 π} (\frac{{\vec{u}}_{z} \land \vec{P_{r} M}}{P_{r} M^{2}} - \frac{{\vec{u}}_{z} \land \vec{Q_{r} M}}{Q_{r} M^{2}}) (3)

Notons que dans le cas du rotor le courant est constant et que la variation dans le temps du champ qu'il crée vient de sa rotation.

La force de Laplace qui s'exerce sur les fils du rotor situés respectivement en P_r et Q_r sont :

\begin{matrix} {\vec{F}}_{P} = i_{r} ℓ {\vec{u}}_{z} \land {\vec{B}}_{s} (P_{r}, t) & (4) \\ {\vec{F}}_{Q} = - i_{r} ℓ {\vec{u}}_{z} \land {\vec{B}}_{s} (Q_{r}, t) & (5) \end{matrix}

Le moment de ces deux forces par rapport à l'axe de rotation est :

\vec{Γ} = \vec{O P_{r}} \land {\vec{F}}_{P} + \vec{O Q_{r}} \land {\vec{F}}_{Q} (6)

Le flux magnétique créé par la spire du rotor à travers celle du stator s'écrit comme une intégrale sur le segment rectiligne $Q_{s} P_{s}$ :

Φ_{s} (t) = ℓ \int_{0}^{1} {\vec{B}}_{r} (M, t) \cdot \vec{n} (Q_{s} P_{s}) d s (7)

où le vecteur unitaire $\vec{n}$ est orthogonale à $Q_{s} P_{s}$ et dirigé vers l'extérieur :

\vec{n} = \frac{\vec{Q_{s} P_{s}} \land {\vec{u}}_{z}}{Q_{s} P_{s}} (8)

On a donc :

Φ_{s} (t) = ℓ \int_{0}^{1} {\vec{B}}_{r} (M, t) \cdot (\vec{Q_{s} P_{s}} \land {\vec{u}}_{z}) d s (9)

La variable d'intégration s étant une abscisse curviligne normalisée variant de 0 à 1, on a :

\vec{O M} = \vec{O Q_{s}} + s \vec{Q_{s} P_{s}} (10)

L'intégrale est calculée numériquement par la méthode des rectangles. La force électromotrice dans le stator (force contre-électromotrice pour un moteur) est donnée par la loi de Faraday :

e_{s} (t) = - \frac{d Φ_{s}}{d t} (11)

On calculera la dérivée suivante :

e'_{s} = - \frac{d Φ_{s}}{d θ_{r}} (12)

qui permettra de calculer la f.é.m. à l'aide de la vitesse angulaire du rotor :

e_{s} (t) = e'_{s} \frac{d θ_{r}}{d t} (13)

On représente un vecteur ou un point par ses trois coordonnées sous la forme d'un tableau. La fonction numpy.cross calcule le produit vectoriel de deux vecteurs.

import numpy as np

class DeuxSpires:
    def __init__(self,a_s,theta_s,alpha_s,a_r,theta_r,alpha_r,longueur,Is=1,Ir=1):
        self.a_s = a_s
        self.theta_s = theta_s
        self.alpha_s = alpha_s
        self.a_r = a_r
        self.theta_r = theta_r
        self.alpha_r = alpha_r
        self.Ir = Ir
        self.Is = Is
        self.longueur = longueur
        self.positions()
        self.uz = np.array([0,0,1])
    def angles(self,theta_s,theta_r):
        self.theta_s = theta_s
        self.theta_r = theta_r
        self.positions()
    def champB(self,i,P,M):
        PM = M-P
        r2 = np.sum(PM*PM)
        return 2e-7*i/r2*np.cross(self.uz,PM)
    def champBstator(self,M):
        return self.champB(self.Is,self.Ps,M)+self.champB(-self.Is,self.Qs,M)
    def champBrotor(self,M):
        return self.champB(self.Ir,self.Pr,M)+self.champB(-self.Ir,self.Qr,M)
    def positions(self):
        self.Pr = np.array([self.a_r*np.cos(self.theta_r+self.alpha_r),self.a_r*np.sin(self.theta_r+self.alpha_r),0])
        self.Qr = np.array([self.a_r*np.cos(self.theta_r-self.alpha_r),self.a_r*np.sin(self.theta_r-self.alpha_r),0])
        self.Ps = np.array([self.a_s*np.cos(self.theta_s+self.alpha_s),self.a_s*np.sin(self.theta_s+self.alpha_s),0])
        self.Qs = np.array([self.a_s*np.cos(self.theta_s-self.alpha_s),self.a_s*np.sin(self.theta_s-self.alpha_s),0])
    def momentRotor(self):
        Fp = self.Ir*self.longueur*np.cross(self.uz,self.champBstator(self.Pr))
        Fq = -self.Ir*self.longueur*np.cross(self.uz,self.champBstator(self.Qr))
        Gamma = np.cross(self.Pr,Fp)+np.cross(self.Qr,Fq)
        return Gamma[2]
    def fluxStator(self,N):
        s = np.arange(0,N)/N
        QsPs = self.Ps-self.Qs
        n = np.cross(QsPs,self.uz)
        f = np.zeros(N)
        for k in range(N):
            M = self.Qs+s[k]*QsPs
            f[k] = np.sum(self.champBrotor(M)*n)
        phi = self.longueur*f.sum()*1/N
        return phi

Voici un exemple, avec tracé du moment en fonction de l'angle $θ_{r}$ :

a_s = 0.1
theta_s = 0
alpha_s = 30/180*np.pi
a_r = 0.08
theta_r = 0
alpha_r = 30/180*np.pi
Is = 100
Ir = 100
longueur = 0.5
spires = DeuxSpires(a_s,theta_s,alpha_s,a_r,theta_r,alpha_r,longueur,Is,Ir)
theta_r = np.arange(360)*2*np.pi/360
Gamma = np.zeros(len(theta_r))
flux = np.zeros(len(theta_r))
N = 100
for k in range(len(Gamma)):
    spires.angles(theta_s,theta_r[k])
    Gamma[k] = spires.momentRotor()
    flux[k] = spires.fluxStator(N)

from matplotlib.pyplot import *
figure(figsize=(16,6))
plot(theta_r*180/np.pi,Gamma)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)

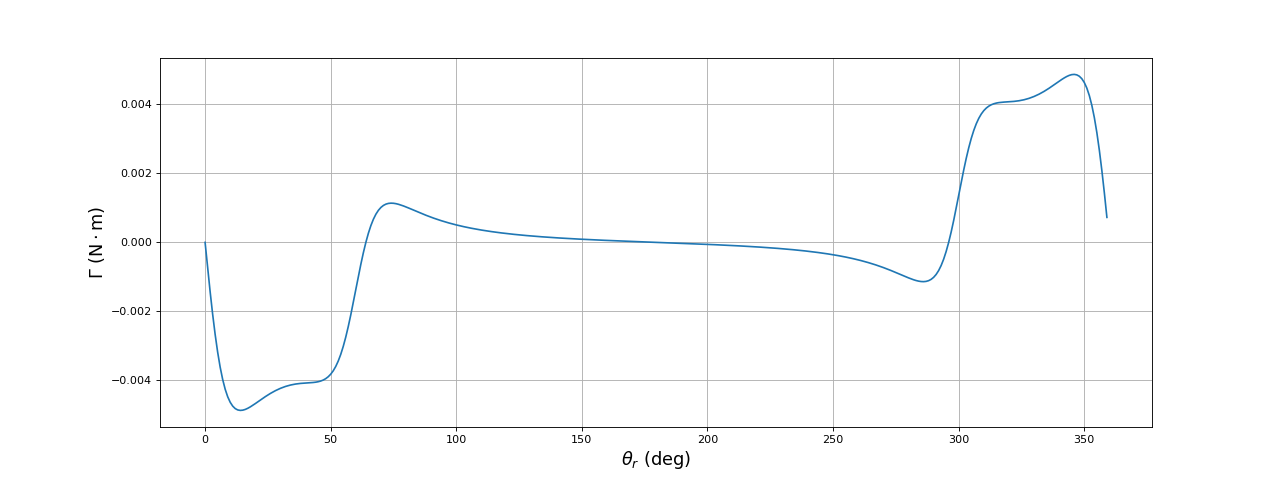fig1.pdf

Voici le flux à travers la spire du stator en fonction de l'angle $θ_{r}$ :

figure(figsize=(16,6))
plot(theta_r*180/np.pi,flux)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$\Phi_s\ (\rm T\cdot m^2)$",fontsize=16)

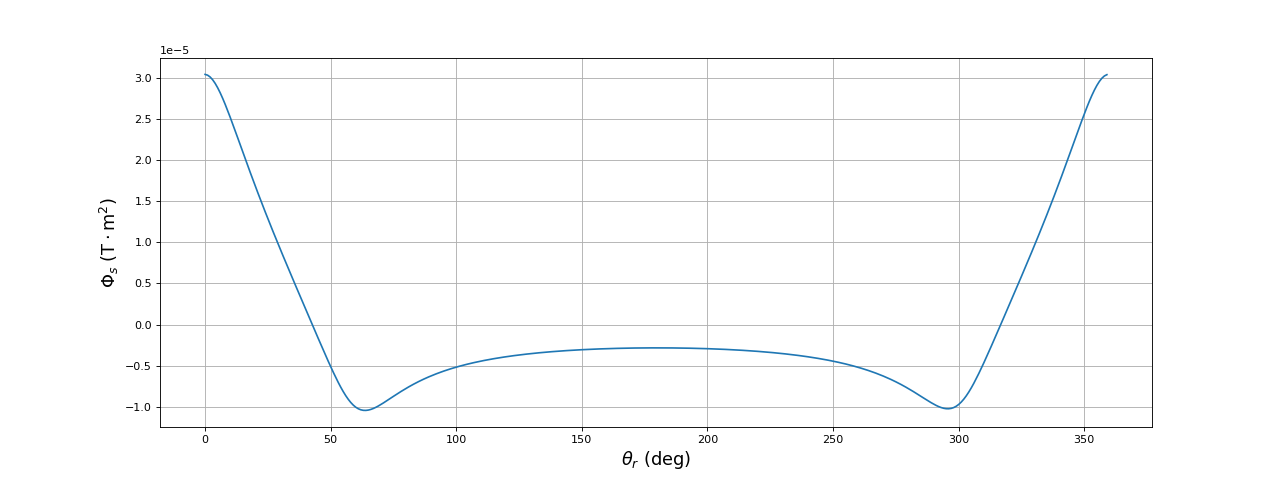fig2.pdf

et la force électromotrice dans la spire du stator :

fem = -np.convolve(flux,[-1,1],mode='valid')/(2*np.pi/len(flux))
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

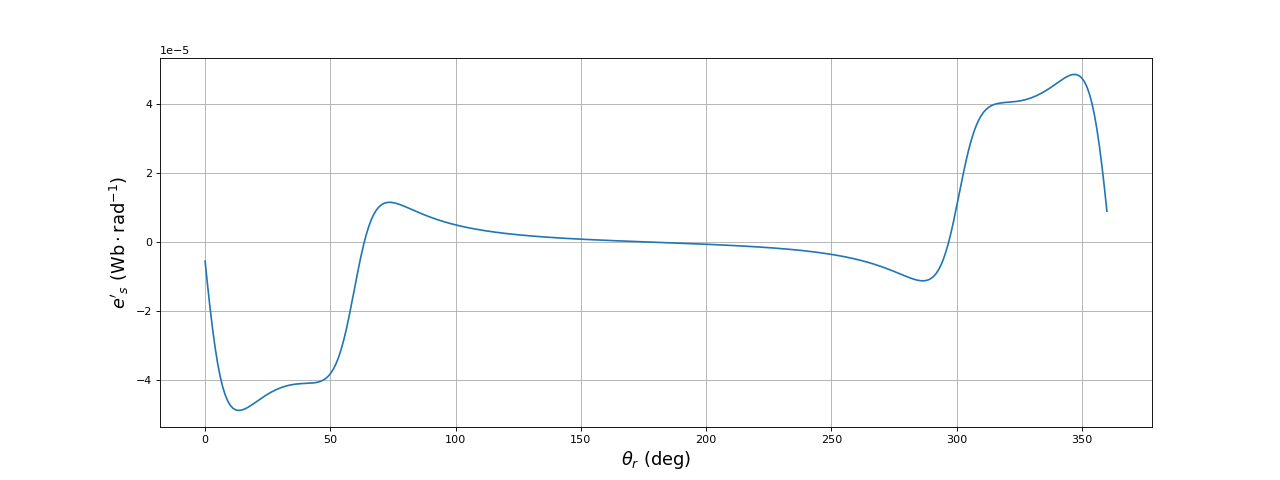fig3.pdf

3. Moteur complet

3.a. Stator bipolaire diphasé et rotor bipolaire

On considère un rotor constitué de 4 bobines (B₁,B₂,B₃,B₄) qui créent un champ bipolaire, c'est-à-dire comportant un pôle nord (N) et un pôle sud (S). Il est possible de créer un champ bipolaire avec seulement deux bobines mais pour créer un champ tournant il faut au moins 3 bobines. Le rotor est constitué de deux bobines (ou deux aimants)) produisant un pôle nord et un pôle sud diamètralement opposés.

Figure pleine page

Deux bobines du stator diamètralement opposées forment une paire de bobines qui sont en réalité deux bobines connectées en série (paire B₁,B₂ et paire B₃,B₄). Le courant circule effectivement dans le même sens par rapport à l'axe dans les deux bobines d'une paire. Les courants dans les deux paires sont en quadrature :

\begin{matrix} i_{s 1} (t) = I_{0} cos (ω t) & (14) \\ i_{s 2} (t) = I_{0} sin (ω t) & (15) \end{matrix}

Ce stator produit un champ tournant bipolaire. À l'instant t=0, la bobine B₁ produit un pôle S au niveau de l'entrefer, la bobine B₂ produit un pôle N. À t=T/4, le pôle S est généré par la bobine B₃ et le pôle N par la bobine B₄. À l'instant t=T/2 le pôle S est généré par la bobine B₂ et le pôle N par la bobine B₁. À l'instant t=3T/4, le pôle S est généré par la bobine B₄ et le pôle N par la bobine B₃. Le rotor génère donc un champ tournant dans le sens trigonométrique à la pulsation $ω$ .

Le rotor comporte une paire de bobines diamètralement opposées parcourues par un courant i_r dans deux sens opposés mais qui sont en fait dans le même sens par rapport à l'axe (Ox). i_r étant supposé positif, ce rotor produit (tel qu'il est orienté sur la figure) un pôle N à droite et un pôle S à gauche. Ce rotor peut aussi être réalisé avec deux aimants fixés sur le bord du rotor. Un seul barreau aimanté centré en O ferait aussi un rotor bipolaire.

La classe DeuxSpires permet de calculer le couple généré par une bobine du stator sur une bobine du rotor. Le couple généré sur une bobine du rotor par l'ensemble du stator est la somme des couples générés par les quatre bobines du stator. Pour obtenir le couple total sur le rotor, il suffira de sommer les couples générés sur ses deux bobines.

On commence par définir le système constitué d'une bobine du rotor et d'une bobine du stator :

a_s = 0.1
theta_s = 0
alpha_s = 30/180*np.pi
a_r = 0.08
theta_r = 0
alpha_r = 30/180*np.pi
Is = 100
Ir = 100
longueur = 0.5
spires = DeuxSpires(a_s,theta_s,alpha_s,a_r,theta_r,alpha_r,longueur,Is,Ir)

Voyons pour commencer le calcul le plus simple, celui de la f.é.m. dans une bobine du stator, en fonction de la position du rotor. On commencer par calculer la f.é.m. générée dans la bobine B₁ du stator par la bobine B_a du rotor, en fonction de l'angle $θ_{r}$ de celle-ci, pour 360 valeurs de l'angle :

theta_r = np.arange(360)*2*np.pi/360
flux = np.zeros(len(theta_r))
N = 100
for k in range(len(theta_r)):
    spires.angles(theta_s,theta_r[k])
    flux[k] = spires.fluxStator(N)
fem_a = -np.convolve(flux,[-1,1],mode='valid')/(2*np.pi/len(flux))
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem_a)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

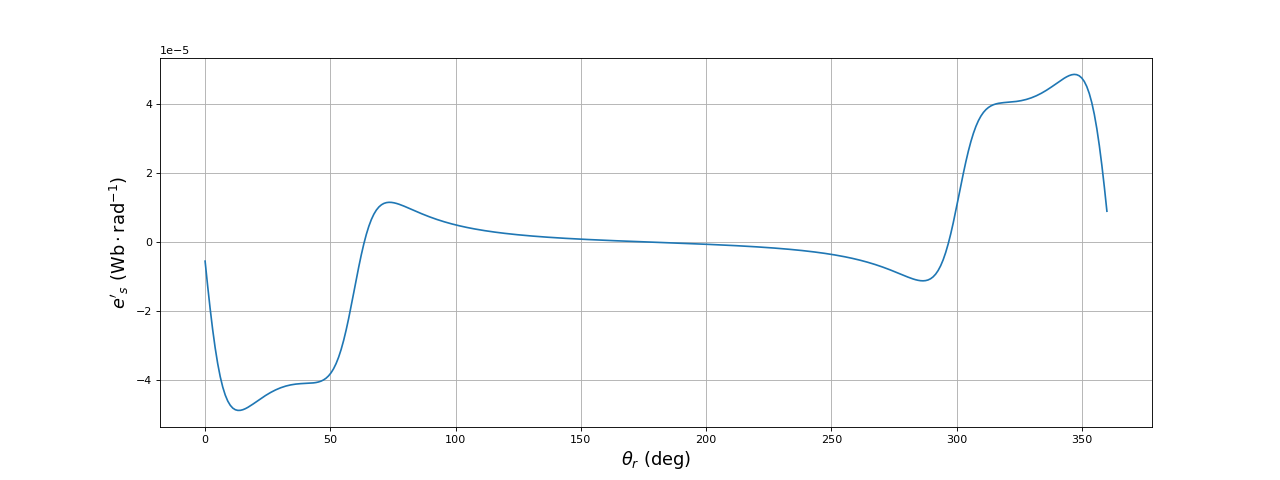fig4.pdf

Lorsque la bobine B_a passe devant la bobine B₁, une f.é.m. positive est générée suivie d'une f.é.m. négative. On remarque cependant que la partie positive est précédée d'une partie négative de moindre amplitude. De même, la partie négative est suivie d'une partie positive de moindre amplitude.

La bobine B_b du rotor est parcourue par un courant opposé à la bobine B_a (voir la figure ci-dessus) et sa position est décalée de 180 degrés par rapport à la première. Pour calculer la f.é.m. que la bobine B_b génère dans la bobine du stator, il suffit de prendre l'opposée de f.é.m. générée par B_a et d'appliquer une rotation de 180 degrés, ce qui se fait simplement avec la fonction numpy.roll :

fem_b  = np.roll(-fem_a,180)
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem_b)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

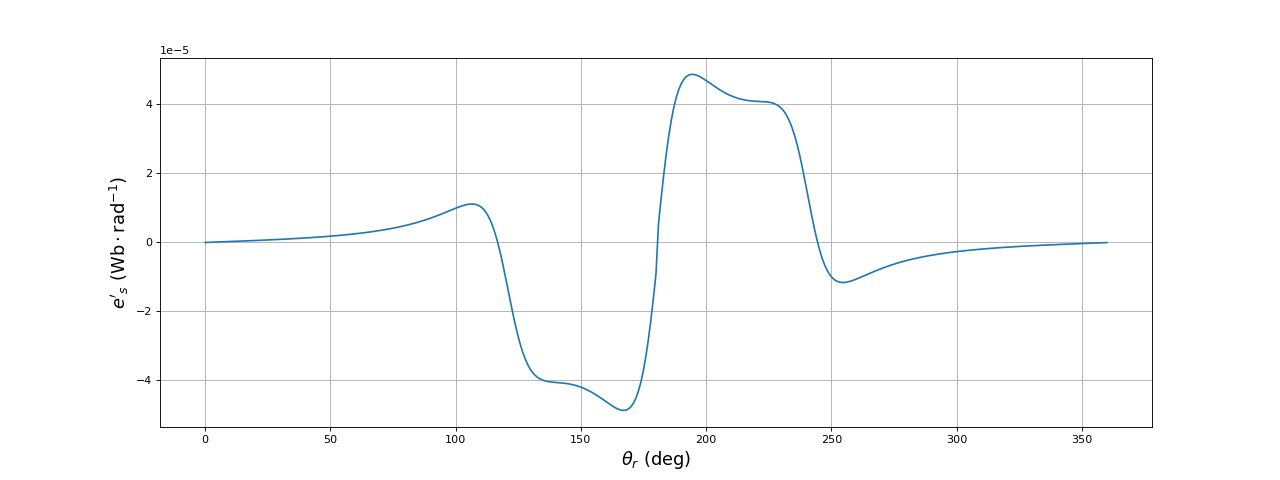fig5.pdf

La f.é.m. totale dans la bobine B₁ est la somme des deux précédentes :

fem_1 = fem_a+fem_b
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem_1)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

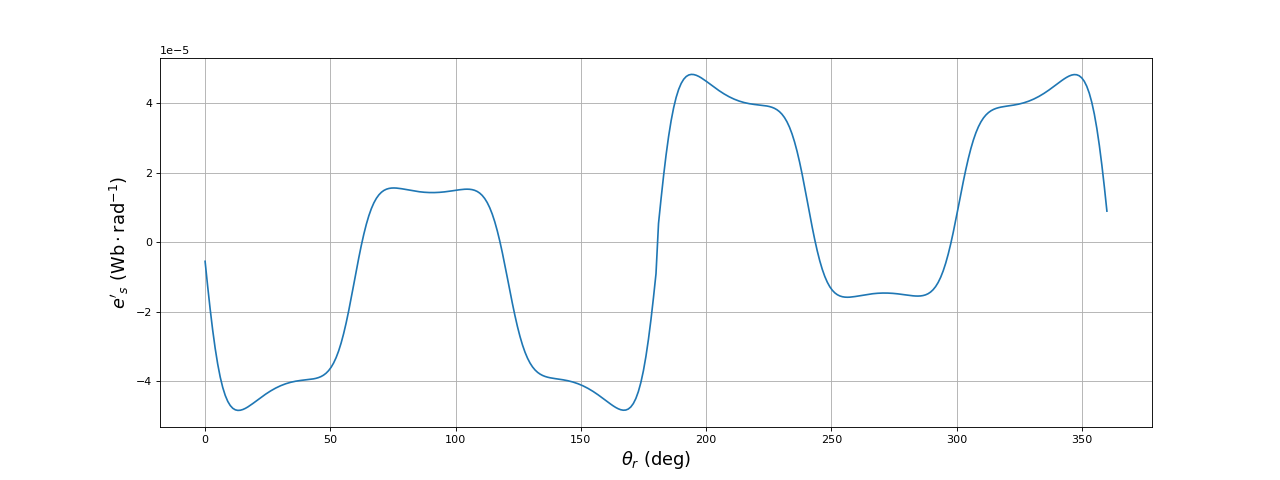fig6.pdf

L'angle reporté en abscisse est l'angle de la bobine B_a du rotor. La f.é.m. générée dans la bobine du stator a une fréquence égale à celle du champ tournant mais sa forme n'est pas optimale car elle ne permet pas de réaliser un générateur donnant une tension quasi sinusoïdale.

Voyons à présent comment calculer le couple moteur sur le rotor. Ce couple dépend à la fois du temps et de la position du rotor. On commence par calculer le couple à l'instant t sur la bobine B_a en fonction de sa position $θ_{r}$ . Pour cela, on calcule le couple généré par chaque bobine du stator et on fait la somme. Le moment généré par chaque bobine du stator doit être multiplié par l'intensité du courant à l'instant considéré dans cette bobine. Le passage de la bobine B_a à la bobine B_b est équivalent à une rotation du rotor de -90 degrés. Le couple total est la somme du couple sur la bobine B_a et de celui sur la bobine B_b. Ce dernier se déduit du précédent par un changement de signe et un décalage de 180 degrés. Le couple sur la bobine B_a est en fait égal au couple sur la bobine B_b.

                          
def couple(t):
    # t = temps divisé par la période
    is1 = np.cos(2*np.pi*t)
    is2 = np.sin(2*np.pi*t)
    Gamma_0 = np.zeros(len(theta_r))
    for k in range(len(theta_r)):
        spires.angles(theta_s,theta_r[k])
        Gamma_0[k] = spires.momentRotor()
    Gamma_a = Gamma_0*is1 + np.roll(Gamma_0*is2,90) + np.roll(Gamma_0*(-is1),180) + np.roll(Gamma_0*(-is2),270)
    Gamma_b = np.roll(-Gamma_a,180)
    Gamma = Gamma_a + Gamma_b
    return Gamma

figure(figsize=(16,6))
subplot(411)
Gamma = couple(0)
plot(theta_r*180/np.pi,Gamma,label='t=0')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(412)
Gamma = couple(0.25)
plot(theta_r*180/np.pi,Gamma,label='t=T/4')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(413)
Gamma = couple(0.5)
plot(theta_r*180/np.pi,Gamma,label='t=T/2')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(414)
Gamma = couple(0.75)
plot(theta_r*180/np.pi,Gamma,label='t=3T/4')
legend(loc='upper right')
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)

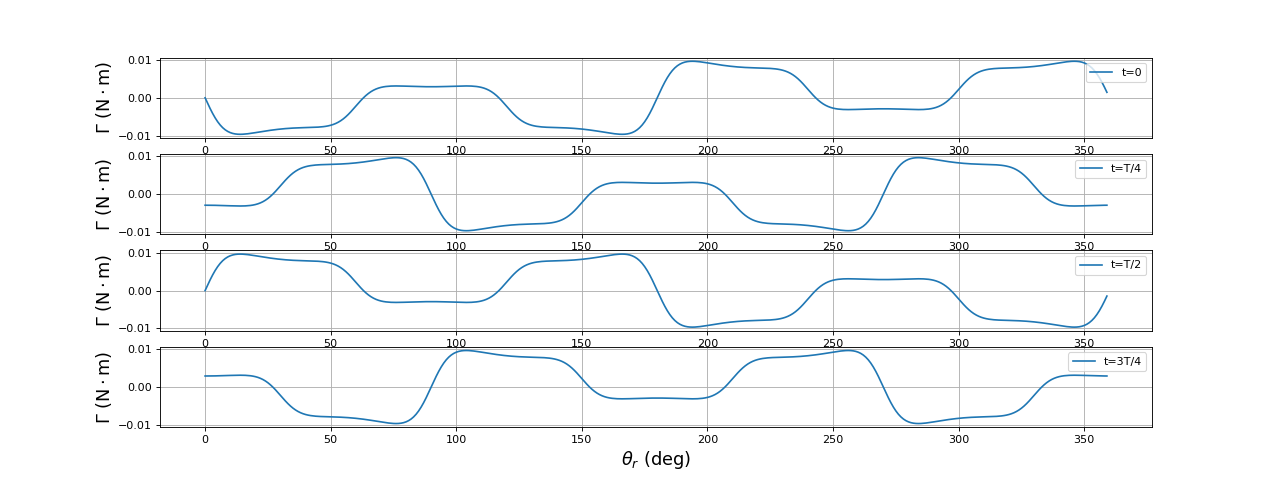fig7.pdf

Le champ tourne à la pulsation $ω_{s}$ . Si le rotor tourne à cette pulsation, le couple moteur est constant. Pour un moteur, il faut que le couple soit du même sens que la rotation : la rotation est ici dans le sens direct (angle croissant), il faut donc un couple positif.

3.b. Stator quadrupolaire monophasé et rotor quadrupolaire

Le stator comporte toujours 4 bobines mais elles sont alimentées de manière à produire 4 pôles (2 pôles N et 2 pôles S) : dans chaque paire, les courants dans les deux bobines sont de sens opposé par rapport à l'axe. On ajoute une paire de bobines au rotor (ou une paire d'aimants) de manière à obtenir un rotor à 4 pôles. Les pôles produits par le stator sont représentés à t=0.

Figure pleine page

Les courants dans les deux paires sont en opposition de phase :

\begin{matrix} i_{s 1} (t) = I_{0} cos (ω t) & (16) \\ i_{s 2} (t) = - I_{0} cos (ω t) & (17) \end{matrix}

Ce stator est donc alimenté par un onduleur monophasé, alors que le stator à 2 pôles nécessite un onduleur diphasé. Contrairement au stator à 2 pôles, le champ produit par ce stator à 4 pôles n'est pas tournant : il y a simplement une inversion des pôles à chaque période du cycle. On remarque par ailleurs que le champ au point O est nul à tout instant car les deux bobines de chaque paire produisent en ce point deux champs opposés.

Remarquons que l'utilisation du stator bipolaire diphasé (produisant un champ tournant) donnerait un couple nul avec ce rotor.

Pour obtenir la f.é.m. générée dans la bobine du stator B₁ en fonction de la position du rotor, il faut sommer les 4 f.é.m. produites par les 4 bobines du rotor. La bobine B_c génère une f.é.m. opposée à celle générée B_a et décalée de 90 degrés. La bobine B_b génère la même f.é.m. que B_a mais décalée de 180 degrés. La bobine B_d génère une f.é.m. opposée à celle générée par B_a et décalée de 270 degrés.

theta_r = np.arange(360)*2*np.pi/360
flux = np.zeros(len(theta_r))
N = 100
for k in range(len(theta_r)):
    spires.angles(theta_s,theta_r[k])
    flux[k] = spires.fluxStator(N)
fem_a = -np.convolve(flux,[-1,1],mode='valid')/(2*np.pi/len(flux))
fem_1 = fem_a+np.roll(-fem_a,90)+np.roll(fem_a,180)+np.roll(-fem_a,270)
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem_1)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

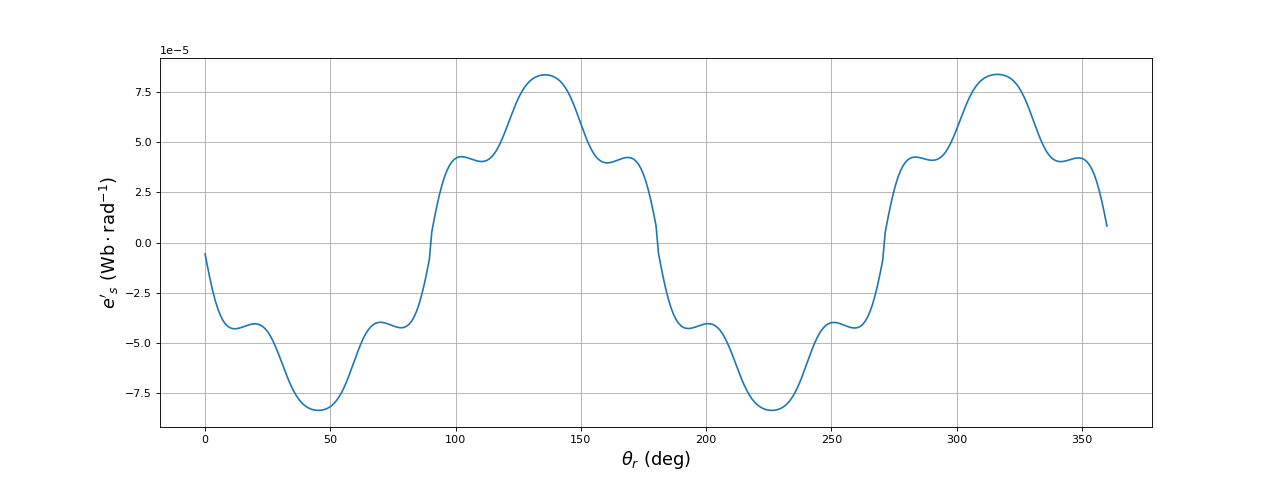fig8.pdf

La présence de 4 pôles dans le rotor permet d'obtenir une f.é.m. s'approchant grossièrement d'une sinusoïde.

Voici les courbes du couple moteur en fonction de la position du rotor, pour 4 instants du cycle du champ tournant :

                          
def couple(t):
    # t = temps divisé par la période
    is1 = np.cos(2*np.pi*t)
    is2 = -is1
    Gamma_0 = np.zeros(len(theta_r)) 
    for k in range(len(theta_r)):
        spires.angles(theta_s,theta_r[k])
        Gamma_0[k] = spires.momentRotor()
    Gamma_a = Gamma_0*is1 + np.roll(Gamma_0*is2,90) + np.roll(Gamma_0*(is1),180) + np.roll(Gamma_0*(is2),270)
    Gamma_b = np.roll(Gamma_a,180)
    Gamma_c = np.roll(-Gamma_a,90)
    Gamma_d = np.roll(-Gamma_a,270)
    Gamma = Gamma_a + Gamma_b + Gamma_c + Gamma_d
    return Gamma

figure(figsize=(16,6))
subplot(411)
Gamma = couple(0)
plot(theta_r*180/np.pi,Gamma,label='t=0')
grid()
ylim(-0.04,0.04)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(412)
Gamma = couple(0.25)
plot(theta_r*180/np.pi,Gamma,label='t=T/4')
grid()
ylim(-0.04,0.04)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(413)
Gamma = couple(0.5)
plot(theta_r*180/np.pi,Gamma,label='t=T/2')
grid()
ylim(-0.04,0.04)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(414)
Gamma = couple(0.75)
plot(theta_r*180/np.pi,Gamma,label='t=3T/4')
legend(loc='upper right')
grid()
ylim(-0.04,0.04)
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)

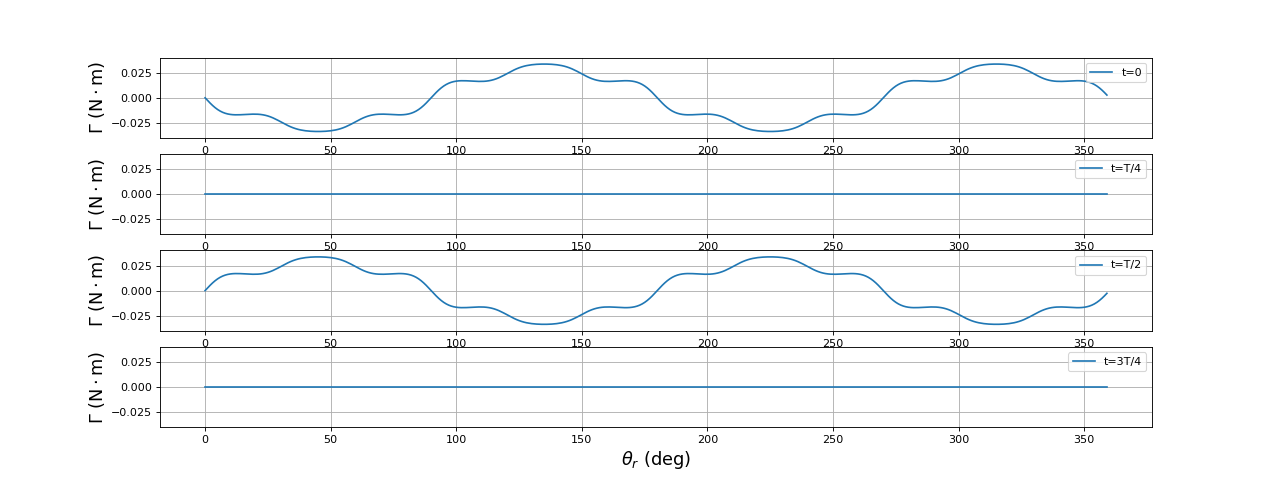fig9.pdf

Le couple est nul à t=T/4 et t=3T/4 quelle que soit la position du rotor car le courant dans les bobines du stator est nul à ces instants. Cette configuration n'est donc pas optimale pour réaliser un moteur car le couple sur le rotor oscille lorsqu'il tourne à la pulsation $ω$ (cela est dû au fait que le champ n'est pas tournant mais simplement pulsant). Son principal avantage est l'alimentation monophasé de son stator. On trouve cette configuration dans certains petits moteurs, par exemple les moteurs de ventilateurs pour PC.

Une configuration similaire à celle-ci mais encore plus simple est composée d'un stator à une paire de bobine et un rotor à une paire (rotor bipolaire et stator bipolaire monophasé).

3.c. Stator bipolaire triphasé et rotor bipolaire

Le stator est composé de trois paires de bobines alimentées par trois courants déphasés de 120 degrés (au moyen d'un onduleur triphasé). Il produit un champ tournant bipolaire. Les trois paires de bobines du stator sont (B₁,B₂), (B₃,B₄) et (B₅,B₆), parcourues par les courants suivants :

\begin{matrix} i_{s 1} (t) = I_{0} cos (ω t) & (18) \\ i_{s 2} (t) = I_{0} cos (ω t + \frac{2 π}{3}) & (19) \\ i_{s 3} (t) = I_{0} cos (ω t - \frac{2 π}{3}) & (20) \end{matrix}

Figure pleine page

Remarquons que dans une paire de bobines du stator, le sens du courant effectif par rapport à l'axe de la paire est le même pour les deux bobines (comme dans le stator diphasé étudié plus haut).

On commence par définir le système constitué d'une bobine du rotor et d'une bobine du stator :

a_s = 0.1
theta_s = 0
alpha_s = 20/180*np.pi
a_r = 0.08
theta_r = 0
alpha_r = 30/180*np.pi
Is = 100
Ir = 100
longueur = 0.5
spires = DeuxSpires(a_s,theta_s,alpha_s,a_r,theta_r,alpha_r,longueur,Is,Ir)

Voici la f.é.m. dans une bobine du stator :

theta_r = np.arange(360)*2*np.pi/360
flux = np.zeros(len(theta_r))
N = 100
for k in range(len(theta_r)):
    spires.angles(theta_s,theta_r[k])
    flux[k] = spires.fluxStator(N)
fem_a = -np.convolve(flux,[-1,1],mode='valid')/(2*np.pi/len(flux))
fem_1 = fem_a+np.roll(-fem_a,180)
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem_1)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

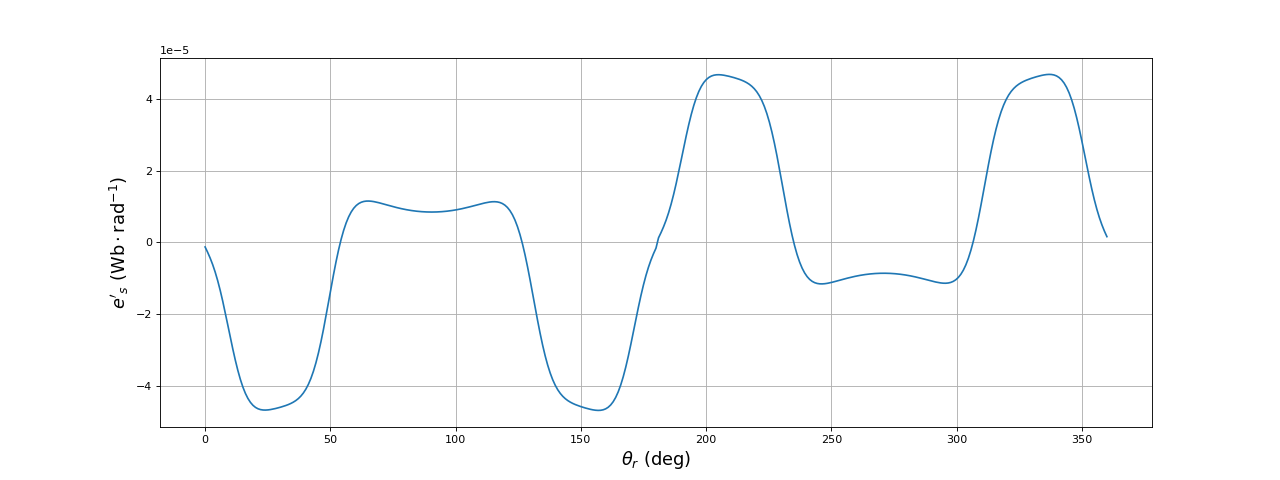fig10.pdf

Comme dans le cas étudié en 3.a, l'utilisation d'un rotor bipolaire fait que la f.é.m. dans une bobine du stator est très loin d'une forme sinusoïdale.

Voici les courbes du couple moteur en fonction de la position du rotor, pour 4 instants du cycle du champ tournant :

                          
def couple(t):
    # t = temps divisé par la période
    is1 = np.cos(2*np.pi*t)
    is2 = np.cos(2*np.pi*t+2*np.pi/3)
    is3 = np.cos(2*np.pi*t-2*np.pi/3)
    Gamma_0 = np.zeros(len(theta_r)) 
    for k in range(len(theta_r)):
        spires.angles(theta_s,theta_r[k])
        Gamma_0[k] = spires.momentRotor()
    Gamma_a = Gamma_0*is1 + np.roll(Gamma_0*(-is1),-180) + np.roll(Gamma_0*is2,-120) + np.roll(Gamma_0*(-is2),60) + np.roll(Gamma_0*is3,120)+np.roll(Gamma_0*(-is3),-60)
    Gamma_b = np.roll(-Gamma_a,-180)
    
    Gamma = Gamma_a + Gamma_b 
    return Gamma

figure(figsize=(16,6))
subplot(411)
Gamma = couple(0)
plot(theta_r*180/np.pi,Gamma,label='t=0')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(412)
Gamma = couple(0.25)
plot(theta_r*180/np.pi,Gamma,label='t=T/4')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(413)
Gamma = couple(0.5)
plot(theta_r*180/np.pi,Gamma,label='t=T/2')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(414)
Gamma = couple(0.75)
plot(theta_r*180/np.pi,Gamma,label='t=3T/4')
legend(loc='upper right')
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)

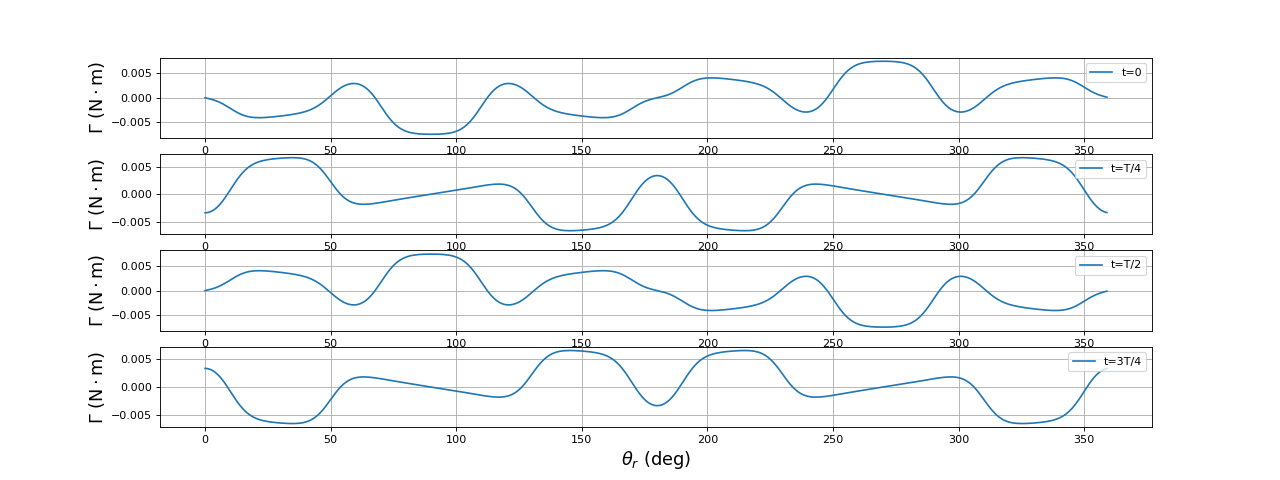fig11.pdf

Le champ tourne à la pulsation $ω_{s}$ . Si le rotor tourne à cette pulsation, le couple moteur est constant.

3.d. Stator quadrupolaire triphasé et rotor quadrupolaire

Comme vu précédemment (partie 3.b), un rotor à 4 pôles permet d'obtenir dans une bobine du stator une f.é.m. plus proche d'une forme sinusoïdale. On peut deviner que l'augmentation du nombre de pôles permettra de s'approcher encore plus de la forme sinusoïdale. L'obtention de 4 pôles au stator avec une alimentation triphasée se fait avec un bobinage plus complexe de ces trois phases. Chaque phase doit alimenter 4 bobines (autant que de pôles). Rappelons que l'on désigne par bobine le système formé de deux fils parcourus par des courants opposés. Les 4 bobines d'une phase doivent être réparties uniformément sur 360 degrés : leurs axes sont donc à 90, 180 et 270 degrés par rapport à la première de chaque phase. L'ensemble des 4 bobines des deux autres phases se déduisent par deux rotations, respectivement de 120 degrés et de -120 degrés. Sur la figure ci-dessous, chaque phase est identifiée par une couleur. Le premier indice d'un nom de bobine identifie la phase, le second identifie le numéro de la bobine pour cette phase.

Figure pleine page

Les 4 bobines alimentées par la phase 1 sont B_1,1,B_1,2,B_1,3,B_1,4 dans l'ordre de la rotation dans le sens trigonométrique. Les sens du courant effectif dans un fil de la bobine B_1,1 et le fil voisin de la bobine B_1,2 sont identiques mais, compte tenu de la convention d'orientation des courants dans les spires, il faut changer le signe du courant algébrique.

Sur la figure, nous avons choisi un angle de 80 degrés pour la largeur angulaire de chaque bobine du stator. Le stator contient 24 fils (12 bobines). Il est souhaitable de répartir ces fils uniformément sur le cercle (chaque fil est en réalité un ensemble de fils logés dans une encoche du stator). L'angle entre deux fils consécutifs est alors de 360/24 degrés et la largeur angulaire d'une bobine est 360/24*5 = 75 degrés.

Il est intéressant de remarquer que les 4 bobines d'une phase sont similaires aux 4 bobines du stator monophasé étudié plus haut (partie 3.b). Ces 4 bobines produisent donc un champ pulsant. La combinaison des 3 phases produit le champ tournant.

On commence par définir le système constitué d'une bobine du rotor et d'une bobine du stator :

a_s = 0.1
theta_s = 0
alpha_s = 37.5/180*np.pi
a_r = 0.08
theta_r = 0
alpha_r = 37.5/180*np.pi
Is = 100
Ir = 100
longueur = 0.5
spires = DeuxSpires(a_s,theta_s,alpha_s,a_r,theta_r,alpha_r,longueur,Is,Ir)

Voici la f.é.m. dans une bobine du stator :

theta_r = np.arange(360)*2*np.pi/360
flux = np.zeros(len(theta_r))
N = 10000
for k in range(len(theta_r)):
    spires.angles(theta_s,theta_r[k])
    flux[k] = spires.fluxStator(N)
fem_a = -np.convolve(flux,[-1,1],mode='valid')/(2*np.pi/len(flux))
fem_1 = fem_a+np.roll(-fem_a,90)+np.roll(fem_a,180)+np.roll(-fem_a,270)
flux_1 = flux + np.roll(-flux,90)+np.roll(flux,180)+np.roll(-flux,270)
figure(figsize=(16,6))
plot(np.linspace(0,360,len(theta_r)-1),fem_1)
#plot(theta_r,flux)
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$e'_s\ (\rm Wb\cdot rad^{-1})$",fontsize=16)

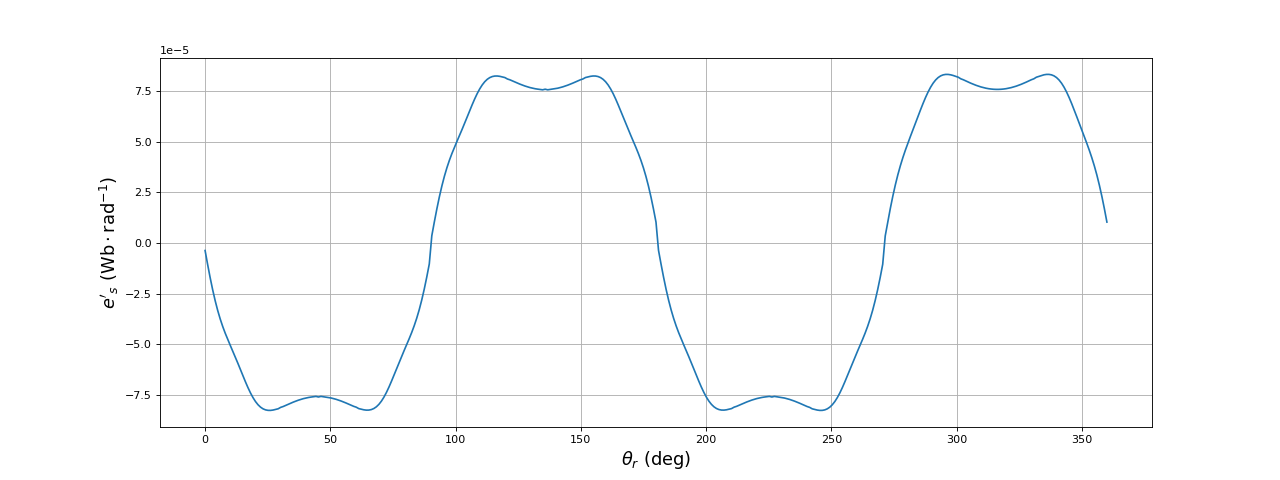fig12.pdf

Voici les courbes du couple moteur en fonction de la position du rotor, pour 4 instants du cycle du champ tournant :

                          
def couple(t):
    # t = temps divisé par la période
    is1 = np.cos(2*np.pi*t)
    is2 = np.cos(2*np.pi*t+2*np.pi/3)
    is3 = np.cos(2*np.pi*t-2*np.pi/3)
    Gamma_0 = np.zeros(len(theta_r)) 
    for k in range(len(theta_r)):
        spires.angles(theta_s,theta_r[k])
        Gamma_0[k] = spires.momentRotor()
    
    Gamma_a = np.roll(Gamma_0*is1,0) + np.roll(Gamma_0*(-is1),90) + np.roll(Gamma_0*is1,180) + np.roll(Gamma_0*(-is1),270)
    Gamma_a += np.roll(Gamma_0*is2,120) + np.roll(Gamma_0*(-is2),90+120) + np.roll(Gamma_0*is2,180+120) + np.roll(Gamma_0*(-is2),270+120)
    Gamma_a += np.roll(Gamma_0*is3,-120) + np.roll(Gamma_0*(-is3),90-120) + np.roll(Gamma_0*is3,180-120) + np.roll(Gamma_0*(-is3),270-120)
    Gamma = Gamma_a + np.roll(-Gamma_a,90) + np.roll(Gamma_a,180) + np.roll(-Gamma_a,270)
    return Gamma

figure(figsize=(16,6))
subplot(411)
Gamma = couple(0)
plot(theta_r*180/np.pi,Gamma,label='t=0')
grid()
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(412)
Gamma = couple(0.25)
plot(theta_r*180/np.pi,Gamma,label='t=T/4')
grid()

ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(413)
Gamma = couple(0.5)
plot(theta_r*180/np.pi,Gamma,label='t=T/2')
grid()

ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)
legend(loc='upper right')
subplot(414)
Gamma = couple(0.75)
plot(theta_r*180/np.pi,Gamma,label='t=3T/4')
legend(loc='upper right')
grid()

xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$\Gamma\ (\rm N\cdot m)$",fontsize=16)

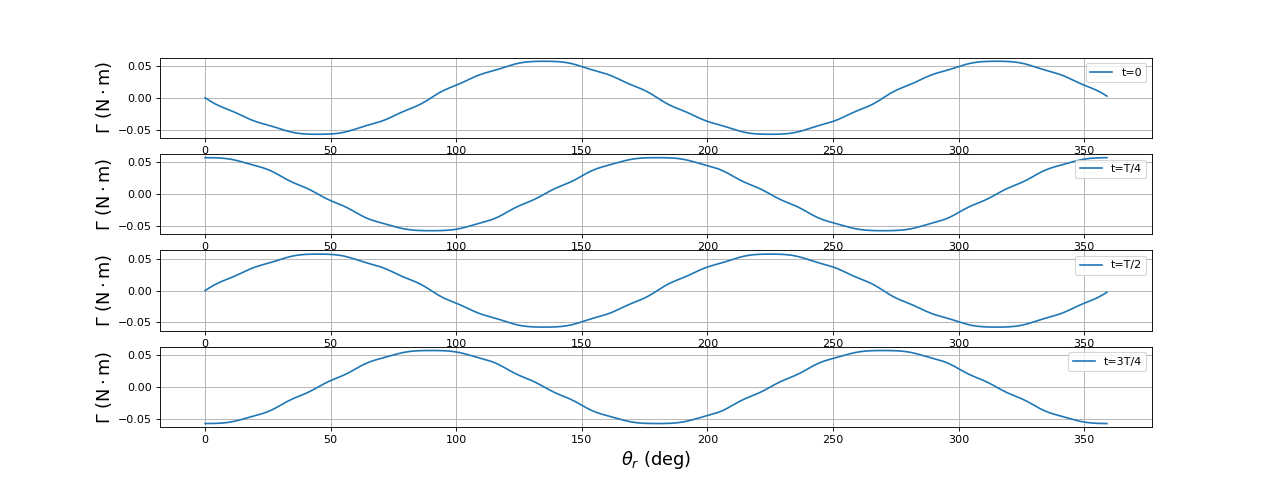fig13.pdf

Le champ tourne à la pulsation $ω_{s} / 2$ . Si le rotor tourne à cette pulsation, le couple moteur est constant.

Ces courbes montrent bien l'avantage d'une machine triphasée à 4 pôles sur une machine triphasée à 2 pôles : la forme de la f.é.m. et celle du couple en fonction de la position du rotor sont proches d'une forme sinusoïdale alors que c'est loin d'être le cas pour la machine à 2 pôles. Pour un moteur, la forme sinusoïdale de la force contre-électromotrice facilite la modélisation du stator. Pour une génératrice, cela permet de générer une tension sinusoïdale.

On peut aussi tracer les composantes radiales et orthoradiales du champ magnétique créé par le stator au niveau du rotor, en fonction de l'angle :

                            
def champB(t):
    is1 = np.cos(2*np.pi*t)
    is2 = np.cos(2*np.pi*t+2*np.pi/3)
    is3 = np.cos(2*np.pi*t-2*np.pi/3)
    theta = np.arange(360)*2*np.pi/360
    champBr_0 = np.zeros(len(theta))
    champBtheta_0 = np.zeros(len(theta))
    for k in range(len(theta)):
        cos = np.cos(theta[k])
        sin = np.sin(theta[k])
        M = np.array([a_r*cos,a_r*sin,0])
        B = spires.champBstator(M)
        champBr_0[k] = B[0]*cos+B[1]*sin
        champBtheta_0[k] = -B[0]*sin+B[1]*cos
    champBr = np.roll(champBr_0*is1,0) + np.roll(champBr_0*(-is1),90) + np.roll(champBr_0*is1,180) + np.roll(champBr_0*(-is1),270)
    champBr += np.roll(champBr_0*is2,120) + np.roll(champBr_0*(-is2),90+120) + np.roll(champBr_0*is2,180+120) + np.roll(champBr_0*(-is2),270+120)
    champBr += np.roll(champBr_0*is3,-120) + np.roll(champBr_0*(-is3),90-120) + np.roll(champBr_0*is3,180-120) + np.roll(champBr_0*(-is3),270-120)
    champBtheta = np.roll(champBtheta_0*is1,0) + np.roll(champBtheta_0*(-is1),90) + np.roll(champBtheta_0*is1,180) + np.roll(champBtheta_0*(-is1),270)
    champBtheta += np.roll(champBtheta_0*is2,120) + np.roll(champBtheta_0*(-is2),90+120) + np.roll(champBtheta_0*is2,180+120) + np.roll(champBtheta_0*(-is2),270+120)
    champBtheta += np.roll(champBtheta_0*is3,-120) + np.roll(champBtheta_0*(-is3),90-120) + np.roll(champBtheta_0*is3,180-120) + np.roll(champBtheta_0*(-is3),270-120)
    return theta,champBr,champBtheta
    
figure(figsize=(16,6))
subplot(411)
theta,champBr,champBtheta = champB(0)
plot(theta,champBr,label=r"$B_r$")
plot(theta,champBtheta,label=r"$B_{\theta}$")
legend(loc='upper right')
grid()
ylabel(r"$B_r\ (\rm T)$",fontsize=16)
subplot(412)
theta,champBr,champBtheta = champB(0.25)
plot(theta,champBr,label=r"$B_r$")
plot(theta,champBtheta,label=r"$B_{\theta}$")
legend(loc='upper right')
grid()
ylabel(r"$B_r\ (\rm T)$",fontsize=16)
subplot(413)
theta,champBr,champBtheta = champB(0.5)
plot(theta,champBr,label=r"$B_r$")
plot(theta,champBtheta,label=r"$B_{\theta}$")
legend(loc='upper right')
grid()
ylabel(r"$B_r\ (\rm T)$",fontsize=16)
subplot(414)
theta,champBr,champBtheta = champB(0.75)
plot(theta,champBr,label=r"$B_r$")
plot(theta,champBtheta,label=r"$B_{\theta}$")
legend(loc='upper right')
grid()
xlabel(r"$\theta_r\ (\rm deg)$",fontsize=16)
ylabel(r"$B_r\ (\rm T)$",fontsize=16)

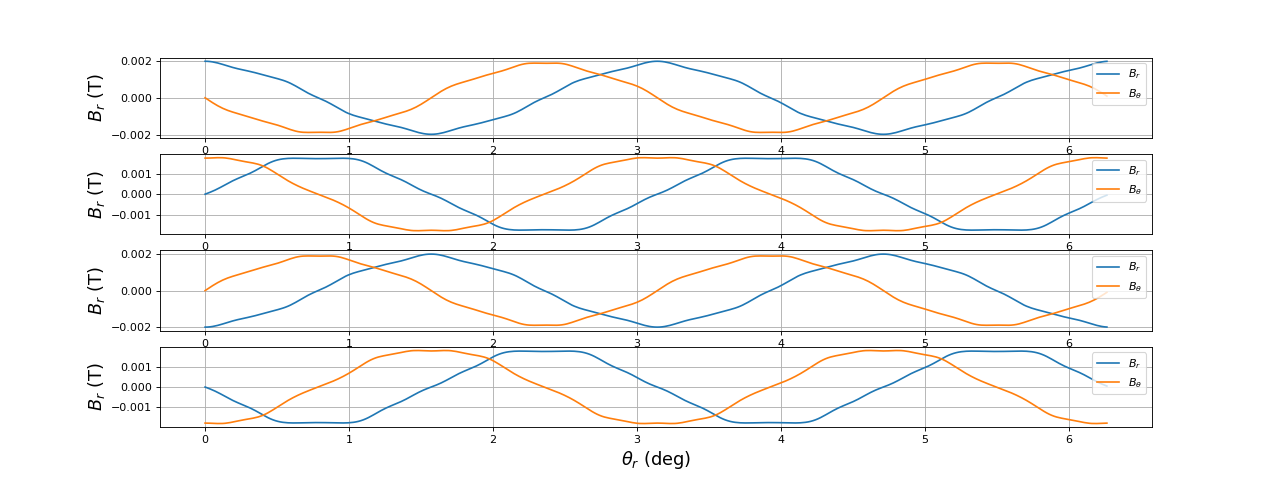fig14.pdf

Sur ces courbes, on voit bien la rotation du champ : il tourne d'un demi-tour pendant une période du courant triphasé. On remarque aussi que le champ dans l'entrefer n'est pas du tout radial. En réalité, la direction du champ dans l'entrefer est très différente de celle-ci en raison de la présence des parties en fer. Notons que seule la composante radial du champ magnétique a un effet sur le couple moteur car elle donne une force de Laplace orthoradiale, alors que la composante orthoradiale donne une force de Laplace radiale.