Ondes électromagnétiques dans un milieu dispersif

1.a. Définitions

Dans un milieu matériel transparent aux ondes électromagnétiques, on considère la propagation d'une onde électromagnétique plane progressive monochromatique (OPPM), de polarisation rectiligne. Le champ électrique a la forme suivante :

$${\underline{E}}_y(x,t)=E_0{e}^{i(kx-\omega t)}\text{(1)}$$

En général, les équations de Maxwell vérifiées par le champ électromagnétique ne sont pas celles du vide. L'équation de propagation n'est donc pas en général l'équation de d'Alembert. Néanmoins, si le milieu est transparent, l'OPPM est solution de l'équation de propagation, mais la relation entre le nombre d'onde k et la pulsation ω n'est pas celle du vide.

La vitesse de phase est définie comme la vitesse de propagation des plans équiphases :

Dans le vide, la vitesse de phase est indépendante de la pulsation, égale à la vitesse de la lumière dans le vide c. Dans un milieu matériel, la vitesse de phase dépend en général de la pulsation.

La matière condensée (solide, liquide) est généralement dispersive pour les ondes électromagnétiques, à des degrés divers en fonction du domaine de fréquence considéré. Dans les gaz, la dispersion est beaucoup plus faible et peut généralement être négligée, à l'exception des milieux gazeux ionisés (plasma), que nous allons étudier plus loin.

Dans le domaine optique, on définit l'indice de réfraction n d'un milieu transparent de la manière suivante :

$$V_{\phi }=\frac{c}{n\left(\omega \right)}\text{(3)}$$

Par extension, on peut définir un indice pour un milieu transparent en général. Lorsque le milieu est dispersif, l'indice de réfraction dépend de la pulsation.

Dans un milieu matériel, on caractérise une onde électromagnétique par sa pulsation (ou sa fréquence), car celle-ci ne change pas lorsque l'onde traverse successivement différents milieux. On peut aussi utiliser la longueur d'onde dans le vide, définie par :

$${\lambda }_0=\frac{c}{f}\text{(4)}$$

Un exemple de milieu dispersif est un verre dans le domaine optique (ou plus généralement tout milieu transparent). L'indice de réfraction dépend de la longueur d'onde dans le vide. C'est pour cette raison que la lumière est dispersée en ses différentes composantes spectrales lorsqu'elle traverse un prisme; l'adjectif dispersif vient de cela. L'indice d'un verre est une fonction décroissante de la longueur d'onde dans le vide. C'est donc une fonction croissante de la pulsation, ce qui signifie que la vitesse de phase est une fonction décroissante de la pulsation. Cette propriété est appelée dispersion normale. Elle est caractéristique des milieux transparents, dans lesquels les ondes électromagnétiques se propagent sans atténuation (les OPPM sont solutions de l'équation de propagation).

1.b. Modulation d'amplitude et vitesse de groupe

Une conséquence du caractère dispersif du milieu est la suivante :

Pour voir cela, nous allons considérer une onde obtenue en superposant deux OPPM de même amplitude, mais ayant des pulsations légérement différentes :

$${\underline{E}}_y(x,t)=E_0(e^{i(k_{1}x-{\omega }_{1}t)}+e^{i(k_{2}x-{\omega }_{2}t)})\text{(5)}$$

Les nombres d'onde sont obtenus avec la relation de dispersion, c'est-à-dire :

$$\begin{array}{ccc}\hfill & k_1=k\left({\omega }_1\right)\hfill & \hfill \text{(6)}\\ \hfill & k_2=k\left({\omega }_2\right)\hfill & \hfill \text{(7)}\end{array}$$

On suppose que l'écart Δω=ω₂-ω₁ est très faible devant la pulsation. On introduit alors la pulsation moyenne ω₀ et on pose :

$$\begin{array}{ccc}\hfill & {\omega }_1={\omega }_0-\frac{\Delta \omega }{2}\hfill & \hfill \text{(8)}\\ \hfill & {\omega }_2={\omega }_0+\frac{\Delta \omega }{2}\hfill & \hfill \text{(9)}\end{array}$$

Pour le nombre d'onde, on effectue un développement limité à l'ordre 1 :

$$\begin{array}{ccc}\hfill & k_1=k\left({\omega }_0\right)-\frac{\Delta \omega }{2}k\text{'}\left({\omega }_0\right)\hfill & \hfill \text{(10)}\\ \hfill & k_2=k\left({\omega }_0\right)+\frac{\Delta \omega }{2}k\text{'}\left({\omega }_0\right)\hfill & \hfill \text{(11)}\end{array}$$

En reportant dans l'expression du champ électrique, on obtient après factorisation :

$${\underline{E}}_y(x,t)=2E_0{e}^{i(k_{0}x-{\omega }_{0}t)}cos\left(\frac{\Delta \omega }{2}(k{\text{'}}_{0}x-t)\right)\text{(12)}$$

Le champ réel s'écrit donc :

$$E_y(x,t)=2E_{0}cos(k_{0}x-{\omega }_{0}t)cos\left(\frac{\Delta \omega }{2}(k{\text{'}}_{0}x-t)\right)\text{(13)}$$

On voit que l'onde résultante est le produit de deux ondes progressives. Le premier cosinus se propage à la vitesse de phase :

$$V_{\phi }=\frac{{\omega }_0}{k_0}\text{(14)}$$

Le second cosinus varie beaucoup plus lentement que le premier, aussi bien dans le temps que dans l'espace. Il constitue donc une modulation de l'amplitude du premier. À x fixé, on a un cosinus de pulsation ω₀ dont l'amplitude est modulée à la pulsation Δω/2. La modulation d'amplitude se propage à la vitesse suivante :

$$V_g=\frac{1}{k\text{'}\left({\omega }_0\right)}=\frac{d\omega }{dk}\left({\omega }_0\right)\text{(15)}$$

Cette vitesse est la vitesse de groupe. C'est l'inverse de la dérivée de la relation de dispersion k(ω), évaluée à la pulsation ω₀. C'est aussi la dérivée de la fonction ω(k).

La vitesse de groupe est la vitesse de déplacement de la modulation, c'est-à-dire de l'enveloppe de l'onde. En terme de transmission des signaux, c'est donc la vitesse de transmission de l'information (valable aussi en modulation de fréquence). D'un point de vue énergétique, on peut montrer que c'est la vitesse de transport de l'énergie.

En dérivant la vitesse de phase par rapport à la pulsation, on obtient :

$$\frac{d{V}_{\phi }}{d\omega }=\frac{1}{k}(1-\frac{V_{\phi }}{V_g})\text{(17)}$$

Lorsque le milieu est dispersif, la vitesse de groupe est donc différente de la vitesse de phase. L'animation Superposition de deux ondes sinusoïdales et dispersion montre l'évolution de l'onde.

1.c. Propagation d'un paquet d'ondes

Comme nous l'avons vu dans le chapitre ondes électromagnétiques dans le vide, on peut construire une succession périodique de paquets d'ondes en superposant des OPPM dont les fréquences sont localisées autour d'une fréquence centrale ω₀. Dans le vide, les paquets d'ondes se propagent sans déformation (l'onde est progressive). Il n'en est plus de même dans un milieu dispersif.

Lorsque le spectre du paquet d'ondes est très étroit, ses composantes spectrales vérifient la relation

$$|\omega -{\omega }_0|\ll {\omega }_0\text{(18)}$$

Dans ce cas, un calcul analogue au précédent (voir paquet d'onde et dispersion) montre que le paquet se propage à la vitesse de groupe, sans que son enveloppe ne se déforme.

Ce résultat repose sur un développement limité à l'ordre 1 de la relation de dispersion. Même lorsque le spectre est très étroit, on observe à plus ou moins long terme un autre phénomène : l'étalement du paquet d'onde.

L'animation ci-dessous utilise la relation de dispersion d'un plasma. Le paquet d'ondes est suivi à la vitesse de groupe pour voir l'évolution de sa forme au cours du temps.

2.a. Définition et exemples

Les deux principales caractéristiques d'un plasma sont sa densité électronique n et sa température T. Les plasmas sont très abondants dans l'univers :

• L'ionosphère, couche de l'atmosphère comprise entre 100 et 600 km d'altitude. La densité est d'environ $n=10^{12}{m}^{-3}$ et la température T=1200 K.
• Le vent solaire, constitué de protons et d'électrons émis par le Soleil.
• La couronne solaire, couche du Soleil s'étendant au delà de la photosphère.
• Le cœur du Soleil.
• Les nébuleuses interstellaires.

Les plasmas artificiels sont aussi nombreux. On peut citer le plasma à l'intérieur d'un tokamak, le plasma dans une lampe à décharge. Dans ce type de lampe, une décharge d'électrons ionise les molécules du gaz et provoque des transitions de niveau électronique.

La physique des plasmas est un domaine d'étude très vaste, car il existe une très grande variété de plasmas. La physique des plasmas relève à la fois de l'électromagnétisme et de la dynamique des fluides (magnéto-hydrodynamique). Le tableau suivant montre comment se situent quelques plasmas sur une échelle logarithmique de densité et de température.

Figure pleine page

Nous allons nous intéresser particulièrement au plasma de l'ionosphère, qui est relativement froid et de très faible densité. Les ions sont produits par des réactions photochimiques sous l'effet du rayonnement solaire UV, très intense à haute altitude. L'ionisation a lieu pendant la journée et la concentration en ions (par conséquent la densité électronique) décroît notablement pendant la nuit. La température dans l'ionosphère est beaucoup plus élevée qu'à la surface terrestre, de l'ordre de 1000 K. L'absorption du rayonnement UV est en grande partie responsable de cette température.

Figure pleine page

2.b. Plasma neutre de faible densité

Globalement, un plasma est neutre puisque les électrons sont issus de l'ionisation des atomes. Cependant, à l'échelle mésoscopique, l'éloignement des charges positives et négatives peut causer l'apparition d'une densité de charge. La longueur de Debye permet de définir l'échelle de neutralité d'un plasma

$${\lambda }_D=\sqrt{\frac{{\epsilon }_0{k}_{B}T}{n{e}^2}}=69\sqrt{\frac{T}{n}}\text{(19)}$$

À une échelle de longueur grande devant la longueur de Debye, on peut considérer que la densité de charge est nulle. Par exemple pour l'ionosphère λ_D=2 mm. Pour l'étude de la propagation d'une onde électromagnétique dans l'ionosphère, on se limite à des longueurs d'onde supérieures au centimètre (radiofréquences). On peut donc poser ρ=0.

Pour déterminer la densité de courant électrique, on suppose que la densité d'électrons n est assez faible pour que l'on puisse négliger les interactions directes entre les charges. La force agissant sur une charge est donc donnée par le champ électromagnétique moyen, c'est-à-dire le champ électromagnétique vue à une échelle très grande devant les distances entre les charges.

$$\overrightarrow{F}=q(\overrightarrow{E}+\overrightarrow{v}\wedge \overrightarrow{B})\text{(20)}$$

En se référant aux ondes électromagnétiques dans le vide, on peut supposer que B sera de l'ordre de grandeur de E/c. On voit donc que si les charges ont une vitesse petite devant celle de la lumière, alors la force magnétique est négligeable devant la force électrique. Nous ferons cette hypothèse, qui nous permet de traiter le mouvement d'une charge (électron ou ion) en suivant la loi de Newton :

$$m\frac{d\overrightarrow{v}}{dt}=q\overrightarrow{E}\text{(21)}$$

Nous allons nous intéresser aux ondes électromagnétiques monochromatiques. On recherche donc une solution permanente de cette équation en régime sinusoïdal. En notation complexe :

$$-i\omega m\overrightarrow{\underline{v}}=q\overrightarrow{\underline{E}}\text{(22)}$$

En distinguant les ions (m_i>10^-27 kg) et les électrons ($m_e=9,1\mathrm{.}10^{-31}kg$), on obtient la densité de courant dans le plasma, en régime sinusoïdal permanent :

$$\overrightarrow{\underline{j}}=i(\frac{n_e{q}_e^2}{\omega m_e}+\frac{n_i{q}_i^2}{\omega m_i})\overrightarrow{\underline{E}}\text{(23)}$$

Pour chaque ion positif, il n'y a que quelques électrons (souvent un seul). Les densités sont donc du même ordre de grandeur. La masse des ions est beaucoup plus grande que celle des électrons donc le courant ionique est négligeable. On obtient ainsi :

La densité de courant complexe de ce modèle de plasma est donc proportionnelle au champ électrique. Cette relation ressemble à la loi d'Ohm locale, mais il faut remarquer que la conductivité est imaginaire pur. Cela signifie que la densité de courant oscille en quadrature par rapport au champ électrique. Considérons alors la puissance moyenne reçue par les charges :

$$<\overrightarrow{j}\cdot \overrightarrow{E}>=\frac{1}{T}{\int }_0^T{j}_0{E}_{0}cos\left(\omega t\right)sin\left(\omega t\right)dt=0\text{(25)}$$

2.c. Équation de propagation

Les équations de Maxwell pour un milieu dont la densité de charge est nulle conduisent à l'équation de propagation suivante :

$${\nabla }^2\overrightarrow{E}={\mu }_0\frac{\partial \overrightarrow{j}}{\partial t}+{\mu }_0{\epsilon }_0\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}\text{(26)}$$

En considérant le régime sinusoïdal permament et en utilisant l'équation $\mathrm{(24)}$, on obtient :

$${\nabla }^2\overrightarrow{\underline{E}}=(\frac{n{e}^2}{{\epsilon }_0{m}_e{c}^2}-\frac{{\omega }^2}{c^2})\overrightarrow{\underline{E}}\text{(27)}$$

2.d. Relation de dispersion

On recherche une solution de l'équation de propagation sous la forme suivante :

$$\overrightarrow{\underline{E}}={\overrightarrow{\underline{E}}}_0{e}^{i(\overrightarrow{\underline{k}}\cdot \overrightarrow{r}-\omega t)}\text{(28)}$$

Le vecteur d'onde sera éventuellement un vecteur complexe. Il s'agit d'une onde plane monochromatique mais si le vecteur d'onde est complexe elle n'est pas progressive. L'équation $\mathrm{(27)}$ conduit à :

$${\underline{k}}^2=\frac{{\omega }^2}{c^2}-\frac{n{e}^2}{{\epsilon }_0{m}_e{c}^2}\text{(29)}$$

On définit alors une pulsation caractéristique du plasma, appelée pulsation de coupure :

$${\omega }_c=\sqrt{\frac{n{e}^2}{{\epsilon }_0{m}_e}}\text{(30)}$$

La relation de dispersion s'écrit finalement :

2.e. Onde plane progressive sinusoïdale

Lorsque ω>ω_c, le vecteur d'onde est réel et la solution $\mathrm{(28)}$ est une onde plane progressive monochromatique. La relation de dispersion s'écrit alors :

$$k=\frac{1}{c}\sqrt{{\omega }^2-{\omega }_c^2}\text{(32)}$$

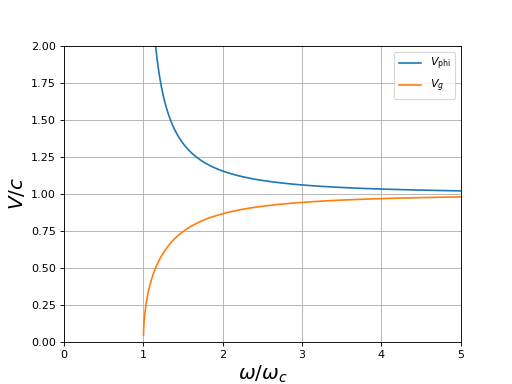
La vitesse de phase est :

$$V_{\phi }=\frac{\omega }{k}=\frac{c}{\sqrt{1-\frac{{\omega }_c^2}{{\omega }^2}}}\text{(33)}$$

On voit que la vitesse de phase dépend de la pulsation : le plasma est un milieu dispersif. Elle est supérieure à la vitesse de la lumière dans le vide. Lorsque la pulsation est très grande devant ω_c, la vitesse de phase est pratiquement égale à celle du vide et la dispersion devient négligeable. À très haute fréquence (par exemple dans l'infrarouge et dans le visible), l'ionosphère se comporte comme le vide. Cela vient du fait que l'inertie des électrons les empêche d'osciller à des fréquences aussi élevées.

2.f. Modulations et paquets d'onde

Comme nous l'avons vu plus haut, les paquets d'onde se propagent à la vitesse de groupe. D'une manière générale, une modulation de l'amplitude se propage à la vitesse de groupe. Pour calculer cette vitesse, dérivons la relation $\mathrm{(31)}$ par rapport à ω :

$$2k\frac{dk}{d\omega }=2\frac{\omega }{c^2}\text{(34)}$$

On obtient ainsi la vitesse de groupe :

$$V_g=\frac{d\omega }{dk}=\frac{c^2}{V_{\phi }}=c\sqrt{1-\frac{{\omega }_c^2}{{\omega }^2}}\text{(35)}$$

La vitesse de groupe est la vitesse de propagation de l'énergie ou de l'information. Elle est strictement inférieure à la vitesse de la lumière dans le vide. Le fait que la vitesse de phase soit supérieure à c n'a aucune conséquence pratique car les ondes rencontrées en réalité ne sont pas parfaitement monochromatiques. L'énergie est nécessairement localisée dans un paquet (plus ou moins grand) dont l'enveloppe se déplace à la vitesse de groupe.

from matplotlib.pyplot import *
import numpy

x = numpy.arange(1.001,5,1e-3)
vg = numpy.sqrt(1-1.0/(x*x))
vp = 1.0/vg

figure()
plot(x,vp,label=r'$V_{\rm phi}$')
plot(x,vg,label=r'$V_g$')
grid()
axis([0,5,0,2])
legend(loc='upper right')
xlabel(r"$\omega/\omega_c$",fontsize=18)
ylabel(r"$V/c$",fontsize=18)
                 

figA.pdf

Lorsqu'on s'approche de la fréquence de coupure, la vitesse de groupe tend vers zéro. Les ondes utilisées pour communiquer avec les satellites doivent avoir une fréquence nettement supérieure à la fréquence de coupure de l'ionosphère. Les fréquences utilisées pour cela sont dans le domaine du gigahertz. Pour de telles fréquences, le plasma ionosphérique est pratiquement équivalent au vide.

2.g. Phénomène de coupure

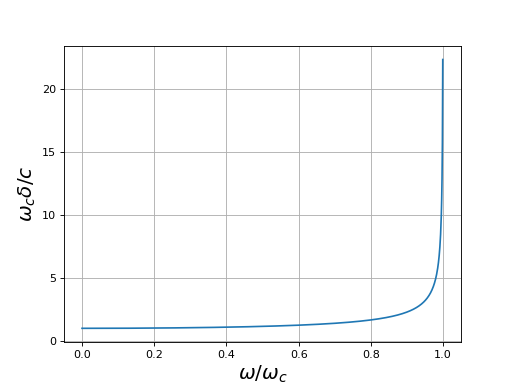
Considérons à présent le cas ω<ω_c. L'équation $\mathrm{(31)}$ conduit alors à un nombre d'onde imaginaire pur :

$$k=\pm i\frac{\sqrt{{\omega }_c^2-{\omega }^2}}{c}=\pm i\frac{1}{\delta }\text{(36)}$$

où δ est une longueur (dépendant de la pulsation). On a donc deux solutions possibles. La solution monochromatique générale est une combinaison linéaire de ces deux solutions. Voici le tracé de δ en fonction de la fréquence. L'unité de longueur est c/ω_c, soit environ 5 m pour l'ionosphère.

x = numpy.arange(0.0,1.0,1e-3)
delta = 1.0/numpy.sqrt(1.0-x*x)
figure()
plot(x,delta)
xlabel(r"$\omega/\omega_c$",fontsize=18)
ylabel(r"$\omega_c\delta/c$",fontsize=18)
grid()
                  

figB.pdf

Considérons une onde plane progressive monochromatique se propageant dans l'air (assimilée au vide) et rencontrant le plasma ionosphérique en incidence normale. On suppose que la polarisation est rectiligne.

Figure pleine page

Pour simplifier, on suppose que l'ionosphère possède une frontière basse bien nette (alors qu'en réalité la densité électronique varie continûment). On place l'origine de z sur cette frontière. Le champ électrique de l'onde incidente (z<0) s'écrit, pour une polarisation rectiligne :

$${\underline{E}}_x(z,t)=E_0{e}^{i(kz-\omega t)}\text{(37)}$$

avec k=ω/c. Dans le plasma, l'onde qui se développe pour z>0 est de la forme :

$${\underline{E}}_x(z,t)=E_1{e}^{-\frac{z}{\delta }}{e}^{-i\omega t}+E_2{e}^{+\frac{z}{\delta }}{e}^{-i\omega t}\text{(38)}$$

Si la pulsation n'est pas trop voisine de la pulsation de coupure, la longueur δ est très petite devant l'épaisseur de l'ionosphère. On peut donc considérer que l'ionosphère est un milieu semi-infini et on ne retient que la solution décroissante :

$$E_x(z,t)=E_1{e}^{-\frac{z}{\delta }}cos\left(\omega t\right)\text{(39)}$$

Cette onde n'est pas progressive, puisque l'amplitude du cosinus s'atténue rapidement avec z. Il s'agit d'une onde évanescente. On peut montrer que cette onde ne transporte aucune puissance (en moyenne). Comme nous l'avons démontré plus haut, aucune énergie n'est dissipée dans ce plasma de très faible densité. En conséquence, la puissance de l'onde incidente n'est pas absorbée dans le plasma mais réfléchie sous forme d'une onde réfléchie se propageant dans le sens de z décroissant, de même amplitude E₀.

En conclusion, le plasma se comporte comme un filtre passe-haut de pulsation de coupure ω_c. Les ondes de pulsation inférieure à la pulsation de coupure sont entièrement réfléchies par le plasma, et ne peuvent donc le traverser.

La simulation Réflexion d'une onde monochromatique sur un plasma montre l'onde réfléchie et l'onde transmise en fonction du rapport ω/ω_c. Le coefficient de réflexion en puissance est égal à 1 en dessous de la pulsation de coupure.

La simulation Réflexion de paquets d'onde sur un plasma montre comment les paquets sont transmis dans le plasma pour ω>ω_c et réfléchis pour ω<ω_c. On remarque la dispersion importante, avec une vitesse de groupe faible, lorsque les raies du paquet sont juste au dessus de la fréquence de coupure.

2.h. Application

Les ondes de fréquence inférieure à environ 9 MHz ne peuvent donc traverser l'ionosphère. Elles sont réfléchies vers le sol. Cette propriété est mise à profit pour la communication à longue distance par onde radio.

Figure pleine page

Les transmissions radiophoniques ondes longues utilisent des fréquences de l'ordre de 100 kHz, qui sont réfléchies par l'ionosphère et par le sol. Les transmissions radio HF de l'ordre du mégahertz utilisent aussi la réflexion par l'ionosphère. Pour les communications par satellites, il faut bien sûr utiliser une fréquence largement supérieure à la fréquence de coupure (de l'ordre du gigahertz).