Mesure de fréquence
1. Introduction
Cette partie montre comment mesurer la fréquence d'un signal TTL, soit par acquisition du signal puis analyse spectrale, soit par utilisation d'un compteur.
La mesure est mise en œuvre avec un multivibrateur astable, afin d'obtenir la valeur de capacité d'un condensateur.
2. Circuit
L'oscillateur utilisé est un multivibrateur astable construit avec un NE555.
Figure pleine pageLes résistances sont R1=R2=8,2 kΩ. Le montage peut être utilisé pour mesurer la capacité C1, qui s'exprime en fonction de la fréquence f d'oscillation par :
La sortie TTL est reliée à l'entrée EA0 de la carte Sysam SP5 et à son entrée CHRONO. La tension aux bornes de C1 sera obtenue sur l'entrée EA1.
Les premières mesures sont faites avec une capacité C1 d'environ 100 nF.
3. Analyse du signal
On commence par l'acquisition de 100000 points à la fréquence d'échantillonnage de 100 kHz :
import pycan.main as pycan
import numpy
sys = pycan.Sysam("SP5")
sys.config_entrees([0,1],[10,10])
te = 10e-6
ne = 100000
sys.config_echantillon(te*1e6,ne)
sys.acquerir()
t=sys.temps()
u=sys.entrees()
sys.fermer()
numpy.savetxt("signal-fe100kHz.txt",[t[0],u[0],u[1]])
import numpy
from matplotlib.pyplot import *
[t,u0,u1] = numpy.loadtxt("signal-fe100kHz.txt")
figure()
plot(t,u0)
plot(t,u1)
grid()
xlabel("t (s)")
ylabel("U (V)")
axis([0,1e-2,0,5])
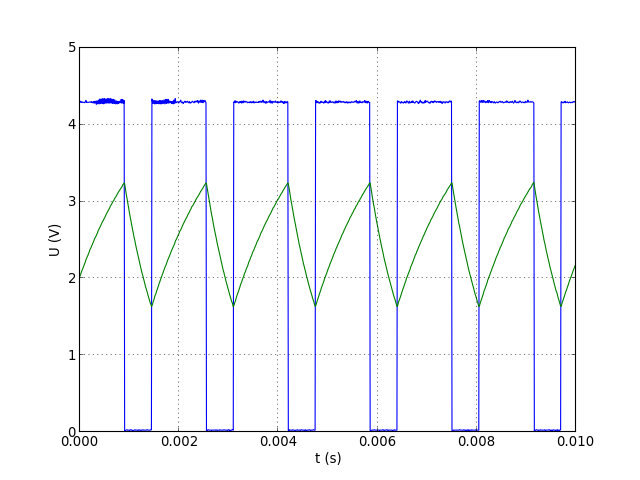figA.pdf
Le signal TTL a un rapport cyclique de 1/3, conformément à la formule :
On fait une analyse spectrale du signal TTL par transformée de Fourier discrète :
import numpy.fft
ne=u0.size
te=t[1]-t[0]
fe=1.0/te
A=numpy.absolute(numpy.fft.fft(u0))/ne
f=numpy.arange(ne)*1.0/(ne*te)
figure()
plot(f,A)
xlabel("f (Hz)")
ylabel("A")
grid()
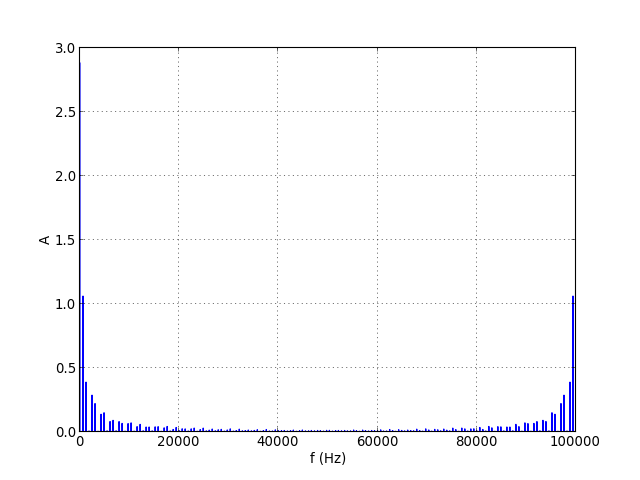figB.pdf
Voici le détail des deux premières raies :
axis([0,2000,0,2])
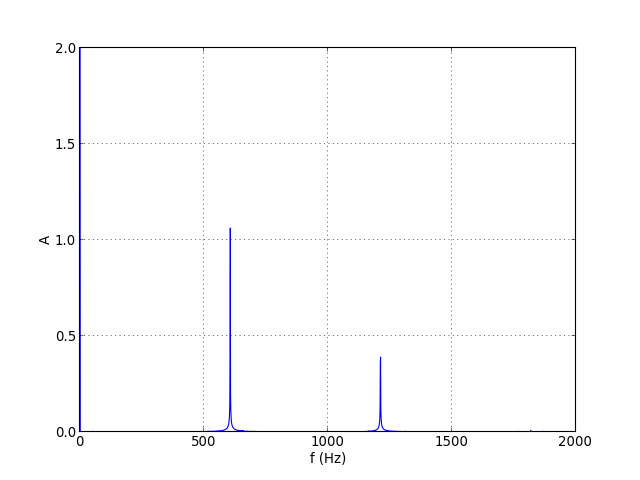figC.pdf
La résolution fréquentielle est l'inverse de la durée de l'acquisition, ici 1 Hz. Pour obtenir la fréquence fondamentale, on isole la partie du spectre comprise entre 100 et 1000 Hz et on recherche l'indice de la valeur maximale :
delta_f=fe/ne
k1 = int(100.0/delta_f)
k2 = int(1000.0/delta_f)
k = numpy.argmax(A[k1:k2])+k1
f0 = k*delta_f
print(f0) --> 606.00000000000011
L'incertitude sur cette fréquence est de 1 Hz. Pour la réduire d'un facteur 10, on fait une acquisition avec une fréquence d'échantillonnage de 10 kHz, le nombre de points étant toujours 100000 :
[t,u0,u1] = numpy.loadtxt("signal-fe10kHz.txt")
figure()
plot(t,u0)
plot(t,u1)
grid()
xlabel("t (s)")
ylabel("U (V)")
axis([0,1e-2,0,5])
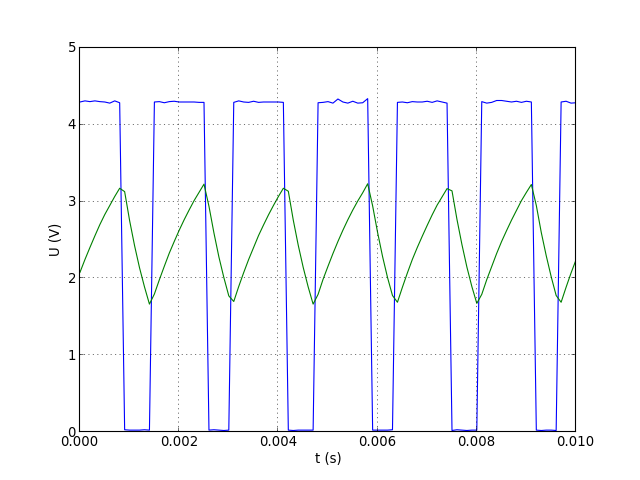figD.pdf
ne=u0.size
te=t[1]-t[0]
fe=1.0/te
A=numpy.absolute(numpy.fft.fft(u0))/ne
f=numpy.arange(ne)*1.0/(ne*te)
figure()
plot(f,A)
xlabel("f (Hz)")
ylabel("A")
grid()
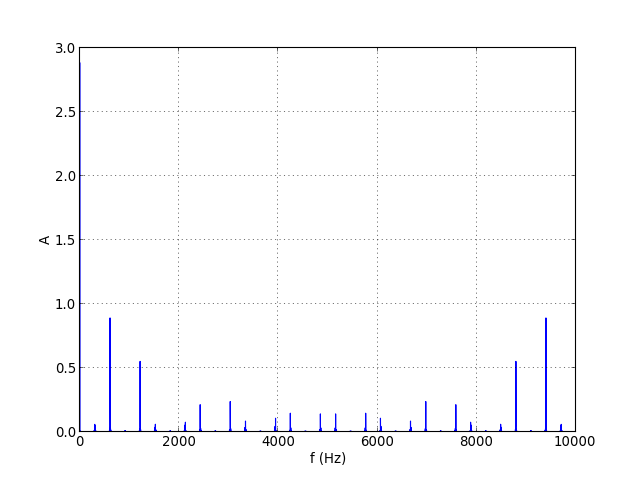figE.pdf
Sur le spectre global, on voit le phénomène de repliement de spectre. Voyons les premières raies :
axis([0,2000,0,2])
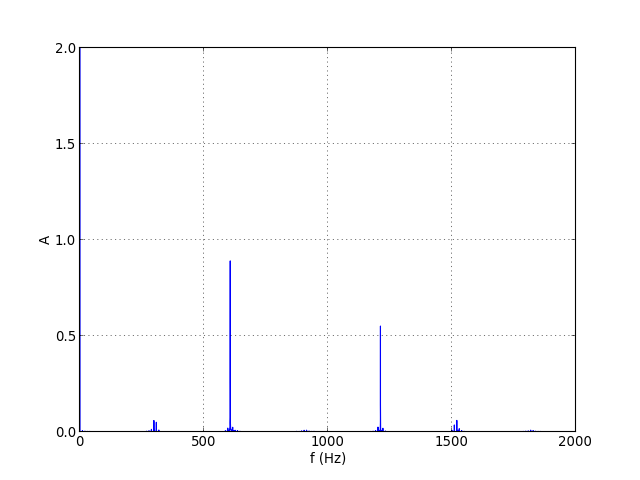figF.pdf
La première raie vers 300 Hz vient du repliement de spectre. Cependant, on extrait sans difficulté la raie fondamentale, qui est toujours la plus haute :
delta_f=fe/ne
k1 = int(100.0/delta_f)
k2 = int(1000.0/delta_f)
k = numpy.argmax(A[k1:k2])+k1
f0 = k*delta_f
print(f0) --> 605.80000000000007
On obtient ainsi la fréquence d'oscillation au dixième de Hertz près (le temps d'acquisition est de 10 secondes).
On en déduit la valeur de la capacité :
R1=R2=8.2e3
C1=1.44/((R1+2*R2)*f0)
print(C1) --> 9.662691542729226e-08
La précision sur la fréquence est bien sûr excessive par rapport à celle sur les résistances. Cependant, l'intérêt de ce montage est de permettre une mesure des faibles variations de capacité d'un capteur capacitif. Une précision relative de 1/1000 sur la mesure de fréquence permet de détecter des variations de capacité relative de 1/1000.
4. Utilisation d'un compteur
Une méthode plus simple de mesure de fréquence d'un signal périodique consiste à utiliser un compteur. La carte Sysam SP5 comporte un compteur dont l'horloge a une période de 10 ns. Le compteur fonctionne sur une durée multiple de cette période, par exemple sur une durée T=10 s. Pendant cette durée, les front montants ou/et descendants sont comptés. Dans notre cas, on peut compter les fronts montants. Voici comment configurer le compteur pour l'entrée CHRONO (qui doit recevoir une tension d'au plus 5 V) :
T=10.0
sys.config_compteur(pycan.ENTREE_CHRONO,front_montant=1,front_descend=0,hysteresis=1,duree=T*1e-6)
La durée est définie en microsecondes. L'hysteresis est une durée pendant laquelle le détecteur de front reste inactif juste après avoir détecté un front. Cela évite de compter plusieurs fronts sur des signaux très bruités. Dans le cas présent, une durée d'hystérésis de 1 μs suffit.
La commande suivante déclenche le compteur :
sys.compteur()
Pendant que le compteur fonctionne (ici 10 s), il est possible d'effectuer d'autres opérations. La commande suivante permet d'attendre la fin du comptage et de récupérer le nombre de fronts montants comptés, et d'en déduire la fréquence :
N = sys.lire_compteur()
f0=N/T
print(f0) --> 605.8
On peut bien sûr se contenter d'une précision moins grande en comptant sur une durée de une seconde ou moins. Si la capacité C1 est de l'ordre du nanofarad, la fréquence d'oscillation est de l'ordre de 60 kHz. On peut alors effectuer la mesure de fréquence en un centième de seconde avec une bonne précision. Voici un programme qui effectue 100 mesures successives de 10 ms :
sys = pycan.Sysam("SP5")
T=0.01
R1=8.2e3
R2=R1
sys.config_compteur(pycan.ENTREE_CHRONO,1,0,1,T*1.0e6)
capa = []
for i in range(100):
sys.compteur()
N=sys.lire_compteur()
f=N/T
C1=1.44/(f*(R1+2*R2))*1e9
capa.append(C1)
sys.fermer()
numpy.savetxt("capa-3.3nF.txt",capa)
capa = numpy.loadtxt("capa-3.3nF.txt")
figure()
plot(capa,'.')
xlabel("n")
ylabel("C (nF)")
axis([0,100,0,5])
grid()
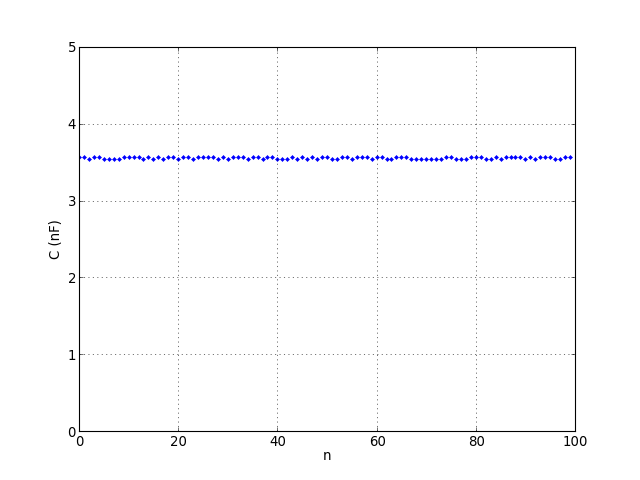figG.pdf
Le nombre de fronts comptés sur chaque mesure est 164. La précision relative de mesure de fréquence est donc inférieure à 1/100.
