CAN Eurosmart

1. Introduction

Cette partie montre comment obtenir la réponse fréquentielle d'un filtre au moyen d'une carte Sysam SP5. La tension appliquée à l'entrée du filtre est générée par la carte et le script Python présenté permet de faire un balayage de la fréquence.

q

2. Dispositif expérimental

Le dispositif permet d'étudier la réponse d'un filtre à un signal délivré par la sortie SA1 de la carte Sysam SP5.

Figure pleine page

La tension d'entrée du filtre est e(t), sa tension de sortie est s(t). À titre d'exemple, nous étudions un filtre constitué d'une bobine et d'un condensateur placés en série, la tension de sortie étant prise aux bornes de ce dernier. Lorsque l'impédance d'entrée du filtre est faible, comme c'est le cas ici au voisinage de la fréquence de résonance, il est nécessaire de placer un amplificateur suiveur entre la sortie SA1 de la carte et l'entrée du filtre.

Le tension e(t) est numérisée sur la voie EA0, la tension s(t) est numérisée du la voie EA1.

3. Méthodes numériques

3.a. Génération de la tension d'entrée

La tension appliquée est sinusoïdale donc les deux signaux ont la forme suivante :

\begin{matrix} e (t) = E cos (ω t) \\ s (t) = S cos (ω t + φ) \end{matrix}

Le convertisseur numérique-analogique de la sortie SA1 fonctionne à la même fréquence d'échantillonnage que le convertisseur analogique-numérique. La fréquence d'échantillonnage maximale pour une utilisation simultanée des entrées et d'une sortie est 1  MHz. Nous pouvons donc en principe générer une sinusoïde jusqu'à une fréquence de 499 kHz en respectant la condition de Nyquist-Shannon.

Notons e_n et s_n les signaux échantillonnés, pour $n = 0, 1, \dots N - 1$ .

Voyons tout d'abord comment les échantillons e_n sont générés. Afin de pouvoir choisir la fréquence f précisément, les N échantillons comportent un nombre variable P de cycles. La fréquence est donc :

f = \frac{P}{N T_{e}} (1)

où T_e est la période d'échantillonnage. Le nombre d'échantillons par période est :

N_{p} = \frac{N}{P} (2)

Ce nombre est en général non entier, ce qui permet justement de faire varier finement la fréquence alors que la période d'échantillonnage ne peut prendre que des valeurs multiples d'une période de base, que nous fixons à 1 microseconde. Dans un premier temps, une valeur approximative de N_p est choisie, par exemple 100, mais cette valeur peut être abaissée lorsque la fréquence est trop grande.

Supposons que l'on ait fixé N et que l'on souhaite une valeur approximative Np et une fréquence freq. On commence par préciser la valeur de la période d'échantillonnage minimale :

teMin=1e-6

Lorsque le nombre Np d'échantillons par période est supérieur au rapport de la période par la période d'échantillonnage minimale, on doit corriger sa valeur :

Np = min(Np,1/(teMin*freq))

La période d'échantillonnage adoptée est un multiple de teMin qui permet d'obtenir environ la fréquence freq avec Np échantillons par période :

techant = int(1/(Np*freq*teMin))*teMin
if techant==0:
        techant = teMin

On calcule la valeur de P, le nombre de périodes pour les N échantillons :

P = int(freq*N*techant)

Pour finir, on calcule la fréquence effective, qui peut être légèrement différente de la fréquence demandée :

freq = P/(N*techant)

et la valeur effective du nombre de points par périodes :

Np=N/P

Cette valeur est différente de la valeur demandée car elle est en général non entière.

Voici comment se fait la génération des N échantillons de tension pour la sortie SA1 :

e1 = amp*np.cos(2*np.pi*P/N*np.arange(N))

Si l'on veut que la fréquence effective soit toujours très proche de la fréquence demandée, il faut que P soit grand et donc il faut que N soit très grand. La valeur N=50000 donne de très bons résultats. La quantité de mémoire interne de la carte Sysam SP5 qu'il faut utiliser est 3N mots de 12 bits, ce qui est largement inférieur à la valeur maximale (262144).

3.b. Traitement des signaux

Soient $\bar{e}$ et $\bar{s}$ les valeurs moyennes des tensions d'entrée et de sortie du filtre. La première est en principe nulle mais la seconde peut avoir une valeur non négligeable par rapport à l'amplitude du signal. Ces valeurs moyennes sont évaluées en calculant la moyenne arithmétique du signal échantillonné :

\begin{matrix} \bar{e} = \frac{1}{N} \sum_{n = 0}^{N - 1} e_{n} \\ \bar{s} = \frac{1}{N} \sum_{n = 0}^{N - 1} s_{n} \end{matrix}

La fonction numpy.mean permet de calculer la valeur moyenne.

L'amplitude efficace du signal retranchée de sa valeur moyenne est l'écart-type des N échantillons :

\begin{matrix} E_{e f f} = \sqrt{\frac{1}{N} \sum_{n = 0}^{N - 1} {(e_{n} - \bar{e})}^{2}} \\ S_{e f f} = \sqrt{\frac{1}{N} \sum_{n = 0}^{N - 1} {(s_{n} - \bar{s})}^{2}} \end{matrix}

La fonction numpy.std permet de calculer l'écart-type.

Le gain du filtre est le rapport des amplitudes efficaces :

G = \frac{S_{e f f}}{E_{e f f}} (3)

Afin de calculer le déphasage entre la sortie et l'entrée, considérons le produit suivant :

\begin{matrix} z (t) = & s (t) (e (t) - j e (t - \frac{T}{4})) \\ = & E S cos (ω t + φ) (cos (ω t) - j sin (ω t)) \\ = & \frac{E S}{2} (e^{j φ} + e^{- j (2 ω t + φ)}) \end{matrix}

Sa valeur moyenne est :

\bar{z} = \frac{E S}{2} e^{j φ} = E_{e f f} S_{e f f} e^{j φ} (4)

Le déphasage cherché est donc l'argument de $\bar{z}$ . On peut aussi calculer la valeur de la fonction de transfert :

\underset{̲}{H} = \frac{\bar{z}}{E_{e f f}^{2}} (5)

Le calcul des échantillons z_n nécessite de disposer du signal $e (t - \frac{T}{4})$ , c'est-à-dire le signal e(t) en avance d'un quart de période. Le nombre d'échantillons de décalage correspondant est la partie entière de N_p/4. Cependant, lorsque N_p est faible, l'obtention précise du signal en quadrature pose problème, à l'exception du cas peu probable où N_p est un nombre entier divisible par 4. Pour résoudre cette difficulté, nous effectuons une augmentation du nombre d'échantillons en procédant à une interpolation par transformée de Fourier. Cette méthode d'interpolation (d'un signal périodique) consiste à calculer la transformée de Fourier discrète du signal (TFD) à N echantillons, à séparer les deux parties conjuguées de taille N/2 puis à ajouter kN zéros entre ces deux parties. On obtient ainsi la TFD d'un signal qui comporte (k+1)N échantillons et qui est obtenu par la transformée de Fourier discrète inverse. Le nombre d'échantillons ajoutés par interpolation entre deux échantillons du signal initial est k.

4. Programme complet

analyseFrequentielle.py

import numpy as np
import matplotlib.pyplot as plt
import pycanum.main as pycan
import numpy.fft

La fonction interpol ci-dessous effectue l'interpolation par transformée de Fourier discrète. x est un tableau contenant le signal échantillonné. Le nombre d'échantillons est multiplié par ninter+1 (ninter contient le paramètre noté k ci-dessus).

def interpol(x,ninter):
    N = len(x)
    tfd = numpy.fft.fft(x)
    N1 = N//2
    tfd2 = np.concatenate((tfd[0:N1],np.zeros(N*ninter),tfd[N1:N]))
    y = np.real(numpy.fft.ifft(tfd2))*(ninter+1)
    return y

La fonction mesure présentée ci-dessous effectue l'acquisition et les calculs pour une fréquence donnée. Ses paramètres sont :

can : objet de la classe Sysam. Les deux entrées utilisées doivent être configurées au préalable.
freq : fréquence souhaitée, en hertz.
amp : amplitude de e(t), en volts.
delai : délai en secondes avant de commencer l'analyse des signaux (pour le régime transitoire).
N : nombre d'échantillons des signaux.
Np : nombre approximatif d'échantillons par période (maximal).
ninter : nombre d'échantillons ajoutés par interpolation.
plot : si True, les signaux e(t) et s(t) sont tracés.

Les valeurs renvoyées sont :

freq : fréquence effective du signal.
G : gain du filtre.
phi : déphasage du filtre, en radians.
H : valeur de la fonction de transfert.
techant : période d'échantillonnage, en secondes.
Np : nombre d'échantillons par période.

def mesure(can,freq,amp,delai,N=50000,Np=100,ninter=4,plot=False):
    teMin = 1e-6
    Np = min(Np,1/(teMin*freq))
    techant = int(1/(Np*freq*teMin))*teMin
    if techant==0:
        techant = teMin
    P = int(freq*N*techant)
    freq = P/(N*techant)
    Np = N/P
    e1 = amp*np.cos(2*np.pi*P/N*np.arange(N))
    can.config_echantillon(techant*1e6,N)
    can.acquerir_avec_sorties(e1,0)
    t=can.temps()[0]
    signaux = can.entrees()
    u=signaux[0]
    s=signaux[1]
    N = len(t)
    n1 = int(delai/techant)
    t=t[n1:N]
    t=t-t[0]
    e=u[n1:N]
    s=s[n1:N]
    N=len(e)
    r = ninter+1
    if ninter>0:
        e = interpol(e,ninter)
        s = interpol(s,ninter)
        t = np.arange(len(e))*t[len(t)-1]/len(e)
    d = int(Np*r/4)       
    E=e.std()
    S=s.std()
    G=S/E
    z=s[d:N]*(e[d:N]-1j*e[0:N-d])
    Z = z.mean()
    phi = np.angle(Z)
    H = Z/E**2
    if plot:
        plt.figure()
        plt.plot(t,e,'b')
        plt.plot(t,s,'r')
        plt.grid()
        plt.ylim(-10,10)
        plt.xlim(0,10/freq)
        plt.show()
    return(freq,G,phi,H,techant,Np)

Voici le script qui permet d'acquérir la réponse fréquentielle du filtre. On commence par ouvrir l'interface avec la carte Sysam SP5 :

can = pycan.Sysam("SP5")

puis on initialise les listes qui serviront à mémoriser les mesures et on définit le tableau des fréquences :

liste_f = []
liste_G = []
liste_phi = []
frequences = np.logspace(2,4,300)

L'amplitude initiale doit être inférieure à 10 V et doit être telle que l'amplitude de la sortie pour la plus faible fréquence soit inférieure à 10 V. Dans le cas du circuit étudié ici, l'amplitude initiale est choisie égale à 2 volts car le montage suiveur avec le circuit LC ne fonctionne pas de manière linéaire pour une amplitude plus grande (à cause de la limite du courant de sortie de l'ALI).

amp0 = 2.0
amp = amp0
delai = 2e-2
ninter=0

Dans la boucle ci-dessous, la mesure pour une fréquence donnée se fait deux fois. La première mesure est faite avec le calibre maximal pour les deux entrées (10 V). Elle permet d'estimer le gain du filtre. Pour la seconde mesure, on ajuste l'amplitude de telle sorte que l'amplitude en sortie ne dépasse par 2 volts (pour d'autres filtres analysés, d'autres stratégies sont possibles). Le calibre des entrées est choisi afin d'offrir le maximum de précision puis la seconde mesure est effectuée, qui donne un résultat plus précis que la première. L'amplitude du signal d'entrée est conservée pour la mesure suivante, ce qui permet d'adapter cette amplitude aux variations du gain. Par exemple pour le circuit LC, l'amplitude diminue à l'approche de la résonance pour s'adapter à la très forte augmentation du gain.

for f in frequences:    
    can.config_entrees([0,1],[10.0,10.0])
    (f,G,phi,H,te,Np) = mesure(can,f,amp,delai,ninter=ninter)
    amp = min(amp0,amp0/G)
    can.config_entrees([0,1],[amp*1.1,amp*G*1.1])
    (f,G,phi,H,te,Np) = mesure(can,f,amp,delai,ninter=ninter,plot=False)
    print("f = %f Hz, G = %f, phi = %f, te = %f, Np = %f"%(f,G,phi,te,Np))
    liste_f.append(f)
    liste_G.append(G)
    liste_phi.append(phi)

On ferme l'interface et on enregistre les mesures dans un fichier :

can.fermer()
np.savetxt('filtreLC-1.txt',np.array([liste_f,liste_G,liste_phi]).T,header='f\t G\t phi')

Le gain en décibel est calculé et on utilise la fonction numpy.unwrap pour éliminer les sauts de phase de 2π. Pour finir, on trace le gain en décibel et le déphasage en fonction de la fréquence, en échelle logarithmique :

GdB = 20*np.log10(liste_G)
liste_phi = np.unwrap(liste_phi)
plt.figure()
plt.plot(liste_f,GdB,'b-')
plt.xscale('log')
plt.grid()
plt.xlabel('f (Hz)')
plt.ylabel('G (dB)')
plt.figure()
plt.plot(liste_f,liste_phi,'b-')
plt.xscale('log')
plt.xlabel('f (Hz)')
plt.ylabel('phi (rad)')
plt.grid()
plt.show()

5. Exemple

On présente ici les résultats pour le filtre LC (bobine d'auto-inductance 45 mH et de résistance 12 Ω, condensateur de 1 μF).

Voici le diagramme de Bode obtenu sans interpolation des signaux :

import numpy as np
from matplotlib.pyplot import *

[liste_f,liste_G,liste_phi] = np.loadtxt('filtreLC-1.txt',unpack=True, skiprows=1)
GdB = 20*np.log10(liste_G)
liste_phi = np.unwrap(liste_phi)

figure(figsize=(8,8))
subplot(211)
plot(liste_f,GdB,'b-')
xscale('log')
grid()
ylabel('G (dB)')
subplot(212)
plot(liste_f,liste_phi,'b-')
xscale('log')
xlabel('f (Hz)')
ylabel('phi (rad)')
grid()

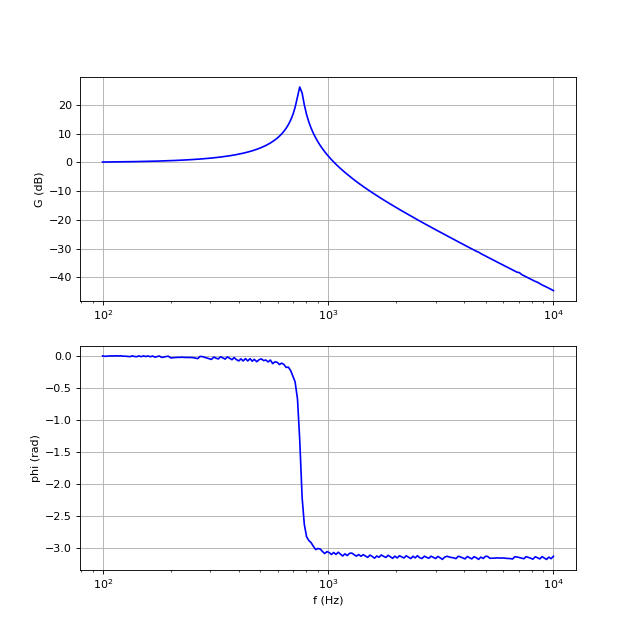bode-1.pdf

Voici le diagramme de Bode obtenu avec ninter=8 :

[liste_f,liste_G,liste_phi] = np.loadtxt('filtreLC-2.txt',unpack=True, skiprows=1)
GdB = 20*np.log10(liste_G)
liste_phi = np.unwrap(liste_phi)

figure(figsize=(8,8))
subplot(211)
plot(liste_f,GdB,'b-')
xscale('log')
grid()
ylabel('G (dB)')
subplot(212)
plot(liste_f,liste_phi,'b-')
xscale('log')
xlabel('f (Hz)')
ylabel('phi (rad)')
grid()

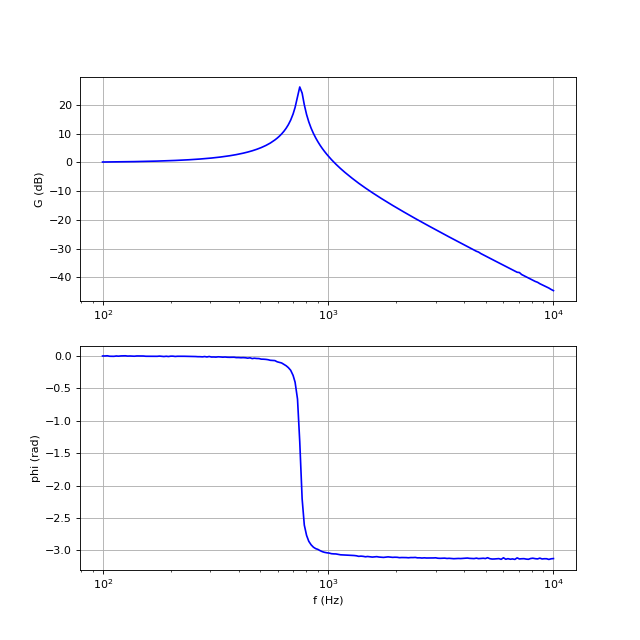bode-2.pdf

L'interpolation permet d'améliorer la précision de la mesure du déphasage.

Diagramme de Bode