Filtres passe-bande analogique et numérique

1. Introduction

Ce document montre l'étude expérimentale d'un filtre analogique passe-bande dont la bande passante est ajustable. Après avoir établi sa réponse à un signal sinusoïdal de fréquence variable et tracé son diagramme de Bode, nous verrons sa caractérisation par la réponse impulsionnelle, qui permet également d'obtenir sa réponse fréquentielle, par tranformée de Fourier.

La second partie montre la mise en œuvre d'un filtre numérique récursif biquadratique, qui permet d'obtenir un filtrage passe-bande similaire à celui du filtre analogique.

2. Filtre passe-bande analogique

2.a. Circuit électronique

Le filtre utilisé est de type Sallen et Key :

Figure pleine page

Le bloc constitué de l'amplificateur, des deux résistances et du potentiomètre à sa droite est un amplificateur de gain K, ajustable entre 4,3 et 5,3 avec le potentiomètre.

La fonction de transfert de ce filtre est :

H (ω) = A \frac{\frac{1}{Q} j \frac{ω}{ω_{0}}}{1 + \frac{1}{Q} j \frac{ω}{ω_{0}} + {(j \frac{ω}{ω_{0}})}^{2}} (1)

avec :

\begin{matrix} A = \frac{K}{5 - K} & (2) \\ ω_{0} = \frac{\sqrt{2}}{R C} & (3) \\ Q = \frac{\sqrt{2}}{5 - K} & (4) \end{matrix}

ω₀ est la pulsation de résonance, correspondant au maximum du gain et à un déphasage nul. Q est le facteur de qualité. La largeur de la bande passante à -3 dB est :

Δ ω = \frac{ω_{0}}{Q} (5)

Le gain maximal est A. Le facteur de qualité augmente avec A selon la relation :

Q = \frac{\sqrt{2}}{5} (1 + A) (6)

En se plaçant en régime sinusoïdal à la fréquence de résonance f₀, le réglage du potentiomètre permet d'obtenir le gain A correspondant au facteur de qualité souhaité.

2.b. Réponse en régime sinusoïdal

Un générateur de signaux (GBF) fournit une tension V_e(t) sinusoïdale. En parallèle avec un suivi des signaux à l'oscilloscope, la carte d'acquisition Sysam SP5 est utilisée pour numériser le signal de sortie V_s(t) et le signal d'entrée. Les entrées EA0 et EA1 de la carte sont branchées respectivement sur l'entrée et la sortie du filtre. Le script suivant effectue l'acquisition de ces deux signaux puis calcule les valeurs efficaces des deux tensions, leur déphasage et la fréquence exacte (par analyse specrale). La fonction mesure(a0,a1,f) effectue ces mesures pour deux calibres de tension et une fréquence approximative donnés. L'utilisateur entre la fréquence approximative du signal, ce qui permet de choisir au mieux la fréquence d'échantillonnage. La fonction mesure est appelée deux fois, la première fois avec le calibre maximal (10  V) afin de déterminer les amplitudes des signaux, la seconde fois avec un calibre choisi en fonction de ces amplitudes. On conserve ainsi une très bonne précision de mesure même lorsque le signal de sortie est très faible (ou inversement). Les mesures sont enregistrées dans un fichier texte.

reponseFrequentielleFiltre.py

import pycanum.main as pycan
import numpy
import numpy.fft
from matplotlib.pyplot import *

sys = pycan.Sysam("SP5")


def mesure(a0,a1,f):
    global sys
    sys.config_entrees([0,1],[a0,a1])
    fe = f*200
    if fe > 1.0e7:
        fe = 1.0e7
    te = 1.0/fe
    ne = 40000
    print("fe = %f"%fe)
    T = ne*te
    print("T = %f"%T)
    sys.config_echantillon(te*1e6,ne)
    sys.acquerir()
    u=sys.entrees()
    t=sys.temps()[0]
    te = t[1]-t[0]
    Ue = u[0]
    Us = u[1]
    calibre_e = max(abs(numpy.max(Ue)),abs(numpy.min(Ue)))
    calibre_s = max(abs(numpy.max(Us)),abs(numpy.min(Us)))
    Ue=Ue-Ue.mean()
    Us=Us-Us.mean()
    spectre = numpy.absolute(numpy.fft.fft(Ue))
    freq = numpy.argmax(spectre[0:int(ne/2)])*1.0/(te*ne)
    print(freq)
    periode = 1.0/freq
    p = int(periode/te/4) # decalage quadrature
    Ve = numpy.roll(Ue,p,0)
    cos = numpy.mean(Ue*Us)
    sin = numpy.mean(Ve*Us)
    phi = -numpy.angle(cos+sin*1j)
    Uemax = numpy.std(Ue)*numpy.sqrt(2)
    Usmax = numpy.std(Us)*numpy.sqrt(2)              
    return (Uemax,Usmax,freq,phi,calibre_e,calibre_s)

liste_freq = []
liste_Ue = []
liste_Us = []
liste_phi = []
liste_freq = []

while True:
    r = input("Frequence approximative (Hz) (taper N pour finir) ?")
    if r=="N":
        break
    f= float(r)
    (a0,a1,f,phi,calibre_e,calibre_s) = mesure(10,10,f)
    (Uemax,Usmax,f,phi,calibre_e,calibre_s) = mesure(10,calibre_s*1.05,f)
    print("f = %.4e, Ue = %.4e, Us = %.4e, phi = %.4e"%(f,Uemax,Usmax,phi))
    liste_freq.append(f)
    liste_Ue.append(Uemax)
    liste_Us.append(Usmax)
    liste_phi.append(phi)
    
sys.fermer()

a_freq = numpy.array(liste_freq)
a_Ue = numpy.array(liste_Ue)
a_Us = numpy.array(liste_Us)
a_phi = numpy.array(liste_phi)


numpy.savetxt("reponseFreq-G30.txt",numpy.array([a_freq,a_Ue,a_Us,a_phi]).T,delimiter="\t",fmt="%.4e",header="f(Hz)\t Ue(V)\t Us(V)\t phi(rad)")

figure()
plot(a_freq,a_Us,"o")
xlabel("f (Hz)")
ylabel("Uc (V)")
grid()

figure()
plot(a_freq,a_phi,"o")
xlabel("f (Hz)")
ylabel("phi (rad)")
grid()

show(block=True)

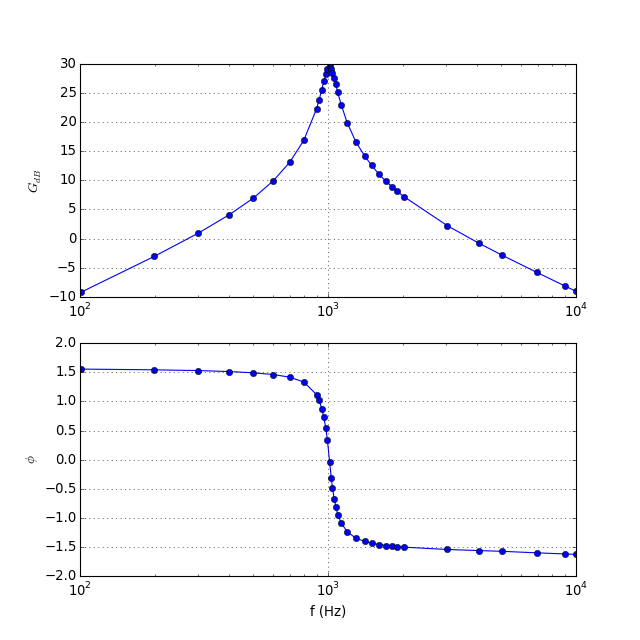
La fréquence de résonance relevée est f₀=1009  Hz. En se plaçant à cette fréquence, le potentiomètre est tournée afin d'obtenir un gain A=30 (soit 29,5  dB), ce qui correspond en théorie à un facteur de qualité Q=8,8. La réponse fréquentielle est déterminée pour des fréquences variant de 100  Hz à 10000  Hz. Voici le gain et le déphasage en fonction de la fréquence :

import numpy
from matplotlib.pyplot import *

[f,Ue,Us,phi]=numpy.loadtxt("reponseFreq-G30.txt",unpack=True,skiprows=1)
G=Us/Ue
GdB=20*numpy.log10(G)
figure(figsize=(8,8))
subplot(211)
plot(f,GdB,'-o')
xscale('log')
ylabel('$G_{dB}$')
grid()
subplot(212)
plot(f,phi,'-o')
xscale('log')
ylabel('$\phi$')
xlabel('f (Hz)')
grid()

figA.pdf

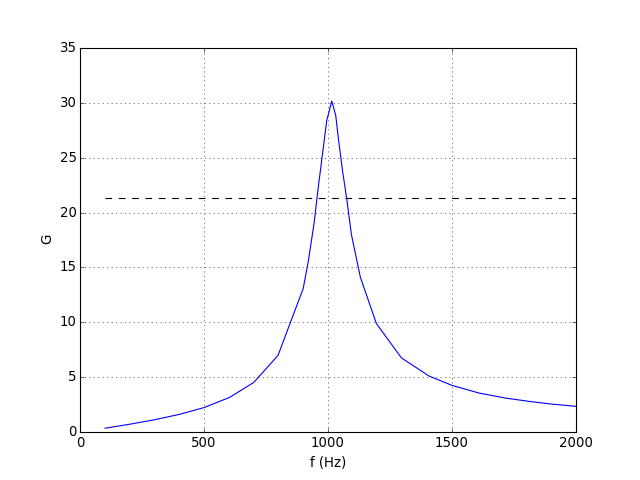
Un tracé du gain G en fonction de la fréquence en échelle linéaire permet de relever plus facilement la largeur de bande passante et le facteur de qualité :

figure(figsize=(8,6))
plot(f,G)
gc=G.max()/numpy.sqrt(2)
xlim(0,2000)
plot([100,2000],[gc,gc],'k--')
xlabel("f (Hz)")
ylabel("G")
grid()

figB.pdf

On relève une largeur de bande passante Δf=120  Hz pour une fréquence de résonance f₀=1009  Hz, soit un facteur de qualité Q=8,4.

2.c. Réponse à un échelon

Théorie

On écrit tout d'abord la fonction de transfert avec la variable s=jω :

H (s) = A \frac{\frac{ω_{0}}{Q} s}{s^{2} + \frac{ω_{0}}{Q} s + ω_{0}^{2}} (7)

L'équation différentielle reliant le signal de sortie au signal d'entrée se déduit de cette forme :

\frac{d^{2} V_{s}}{d t^{2}} + \frac{ω_{0}}{Q} \frac{d V_{s}}{d t} + ω_{0}^{2} V_{s} = A \frac{ω_{0}}{Q} \frac{d V_{e}}{d t} (8)

D'une manière générale (quelque soit le signal d'entrée) la résolution de cette équation nécessite les racines de l'équation :

s^{2} + \frac{ω_{0}}{Q} s + ω_{0}^{2} = 0 (9)

c'est-à-dire les pôles de la fonction de transfert H(s). On se place dans le cas Q>1/2 où les deux pôles p₁ et p₂ sont complexes conjugués :

p_{i} = - \frac{ω_{0}}{2 Q} \pm j ω_{0} \sqrt{1 - \frac{1}{4 Q^{2}}} (10)

Lorsque Q>5, on peut utiliser l'approximation suivante :

p_{i} \approx - \frac{ω_{0}}{2 Q} \pm j ω_{0} (11)

La réponse à un échelon a donc la forme suivante :

V_{s} (t) = exp (- \frac{ω_{0}}{2 Q} t) (A_{1} cos (ω_{0} t) + A_{2} cos (ω_{0} t)) (12)

Il s'agit d'oscillations amorties de pulsation ω₀. Après un nombre d'oscillations égal au facteur de qualité, le facteur exponentiel est égal à :

exp (- \frac{ω_{0}}{2 Q} \frac{2 π Q}{ω_{0}}) = exp (- π) = 0, 043 (13)

Une estimation rapide du facteur de qualité à partir de la réponse à un échelon expérimentale peut être faite en comptant les oscillations jusqu'à réduction à 4,3% de l'amplitude maximale. Pour une détermination plus précise, la méthode du décrément logarithmique doit être utilisée. Elle consiste à relever le rapport x des deux maxima entre lesquels il y a n oscillations. Le facteur de qualité est alors :

Q = \frac{π n}{ln (x)} (14)

Expérience

La réponse à un échelon s'observe facilement avec un GBF délivrant une tension carrée dont la période est plus grande que le temps de réponse du filtre. Nous pouvons aussi utiliser la sortie SA1 de la carte Sysam SP5 pour délivrer un échelon simultanément à l'acquisition des tensions d'entrée et de sortie du filtre. Voici le script réalisant cela :

acquisitionReponseEchelon.py

import pycanum.main as pycan
import numpy
from matplotlib.pyplot import *
sys=pycan.Sysam("SP5")
sys.ouvrir()

te=1e-6
T=5e-2 # durée de l'acquisition
N=int(T/te)
sortie1 = numpy.zeros(N)
sortie2 = numpy.zeros(N)
debut=T*0.1 # début de l'échelon
n1=int(debut/te)
sortie1[n1:N-1] = 1

sys.config_entrees([0,1],[10,10])
sys.config_echantillon(te*1e6,N)
sys.acquerir_avec_sorties(sortie1,sortie2)
temps=sys.temps()
tensions=sys.entrees()
t=temps[0]
u0=tensions[0]
u1=tensions[1]
sys.fermer()


figure()
plot(t,u0)
plot(t,u1)
xlabel("t (s)")
ylabel("u (V)")
grid()
axis([0,t.max(),-10,10])

numpy.savetxt("reponseEchelon-SP5-G30.txt",numpy.array([t,u0,u1]).T,fmt='%0.4e',header='t(s) u0(V) u1(V)',delimiter='\t')

show()

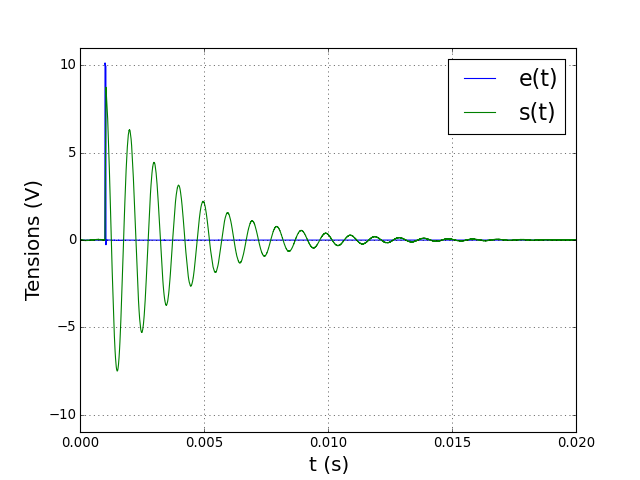
Voici la réponse à un échelon obtenue avec le filtre précédent :

[t,ue,us]=numpy.loadtxt("reponseEchelon-SP5-G30.txt",unpack=True,skiprows=1)
figure()
xlabel("t (s)")
ylabel("Tensions (V)")
plot(t,ue,label="e(t)")
plot(t,us,label="s(t)")
grid()
xlim(0,0.02)
ylim(-4,4)
legend(loc="upper right",fontsize=20)

figC.pdf

Le rapport des maxima pour n=7 est x=12,15, ce qui conduit à un facteur de qualité Q=8,8, identique à la valeur calculée plus haut à partir du gain maximal. En modifiant le réglage du gain K du filtre, on observe la variation du nombre d'oscillations.

2.d. Réponse impulsionnelle

Théoriquement, la réponse impulsionnelle est obtenue en appliquant en entrée une impulsion de largeur nulle est de hauteur infinie (impulsion de Dirac). La réponse impulsionnelle d'un filtre passe-bande du second ordre présente une forme similaire à la réponse à un échelon, avec une décroissance exponentielle déterminée par le facteur de qualité comme précédemment. Un autre intérêt de la réponse impulsionnelle vient du spectre parfaitement plat de l'impulsion de Dirac, dont la transformée de Fourier est égale à 1. En conséquence, la transformée de Fourier de la réponse impulsionnelle est égale à la réponse fréquentielle de filtre.

Expérimentalement, on doit bien sûr appliquer une impulsion de durée finie, petite par rapport aux échelles de temps de la réponse impulsionnelle, mais assez grande pour obtenir une réponse notable. Après numérisation, on réalise la transformée de Fourier discrète de la réponse impulsionnelle afin d'obtenir la réponse fréquentielle du filtre.

Le script suivant permet d'obtenir la réponse à une impulsion dont la durée est très courte par rapport à la période d'oscillation :

acquisitionReponseImpulsionnelle.py

 import pycanum.main as pycan
import numpy
from numpy.fft import fft
from matplotlib.pyplot import *
sys=pycan.Sysam("SP5")
sys.ouvrir()

te=1e-6
T=5e-2 # durée de l'acquisition
N=int(T/te)
sortie1 = numpy.zeros(N)
sortie2 = numpy.zeros(N)
duree=4e-5 # durée de l'impulsion
n=int(duree/te)
debut=1e-3 # début de l'impulsion
n1=int(debut/te)
sortie1[n1:n1+n] = 10

sys.config_entrees([0,1],[10,10])
sys.config_echantillon(te*1e6,N)
sys.acquerir_avec_sorties(sortie1,sortie2)
temps=sys.temps()
tensions=sys.entrees()
t=temps[0]
u0=tensions[0]
u1=tensions[1]
sys.fermer()


figure()
plot(t,u0)
plot(t,u1)
xlabel("t (s)")
ylabel("u (V)")
grid()
axis([0,t.max(),-10,10])

tfd0 = fft(u0)*2/N
spectre0 = numpy.absolute(tfd0)
tfd1 = fft(u1)*2/N
freq = numpy.arange(N)*1.0/T
spectre1 = numpy.absolute(tfd1)

figure()
plot(freq,spectre0,".")
plot(freq,spectre1,".")
xlabel("f (Hz)")
ylabel("Volt")
grid()
axis([0,1e4,0,spectre1.max()])

figure()
gain = spectre1/spectre0
plot(freq,20*numpy.log10(gain))
xlabel("f (Hz)")
ylabel("dB")
xscale('log')
grid()
xlim(1e2,1e4)
ylim(-60,40)

numpy.savetxt("reponseImp-G30.txt",numpy.array([t,u0,u1]).T,fmt='%0.4e',header='t(s) u0(V) u1(V)',delimiter='\t')

show()

Voici la réponse impulsionnelle expérimentale :

[t,ue,us]=numpy.loadtxt("reponseImp-G30.txt",unpack=True,skiprows=2)

figure()
xlabel("t (s)",fontsize=18)
ylabel("Tensions (V)",fontsize=18)
plot(t,ue,label="e(t)")
plot(t,us,label="s(t)")
grid()
xlim(0,0.02)
ylim(-11,11)
legend(loc="upper right",fontsize=20)

figC.pdf

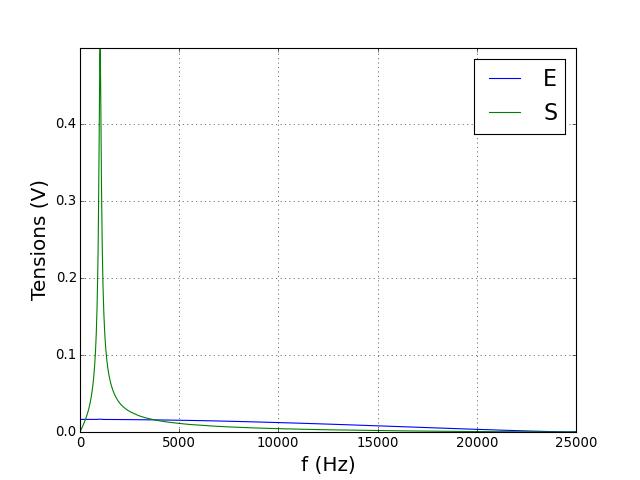
Traçons les spectres de l'entrée et de la sortie. La fréquence d'échantillonnage étant de 1  MHz, les spectres s'étendent en principe jusqu'à 500  kHz. La durée de l'impulsion de 40  μs impose toutefois de ne pas dépasser 25  kHz.

from numpy.fft import fft
N=len(ue)
T=t[N-1]
tfd_e = fft(ue)*2/N
spectre_e = numpy.absolute(tfd_e)
tfd_s = fft(us)*2/N
freq = numpy.arange(N)*1.0/T
spectre_s = numpy.absolute(tfd_s)

figure()
plot(freq,spectre_e,label="E")
plot(freq,spectre_s,label="S")
xlabel("f (Hz)",fontsize=18)
ylabel("Tensions (V)",fontsize=18)
grid()
legend(loc="upper right",fontsize=20)
axis([0,25000,0,spectre_s.max()])

figD.pdf

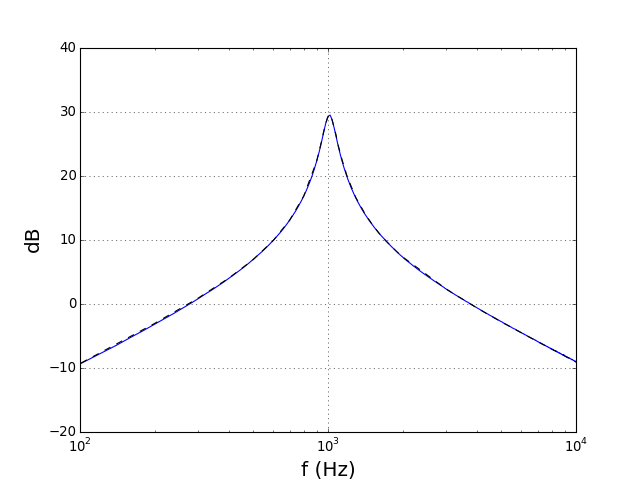
Sur la bande de fréquence [0,10000]  Hz, le spectre de l'impulsion d'entrée prend une valeur pratiquement constante. On divise le spectre de la sortie par celui de l'entrée afin d'obtenir la réponse fréquentielle du filtre dans cette bande de fréquences :

gain=spectre_s/spectre_e
figure()
plot(freq,20*numpy.log10(gain))
plot(f,GdB,"k--")
xlabel("f (Hz)",fontsize=18)
ylabel("dB",fontsize=18)
xscale('log')
grid()
xlim(1e2,1e4)
ylim(-20,40)

figE.pdf

Pour comparaison, la courbe obtenue plus haut par analyse en régime sinusoïdal a été ajoutée (en pointillé).

3. Filtre numérique passe-bande

3.a. Conception du filtre

Un filtre numérique passe-bande similaire au filtre analogique précédent peut être réalisé au moyen d'un filtre récursif, défini par une relation de récurrence de la forme suivante :

y_{n} = b_{0} x_{n} + b_{1} x_{n - 1} + b_{2} x_{n - 2} - a_{1} y_{n - 1} - a_{2} y_{n - 2} (15)

La fonction de transfert en Z d'un tel filtre est :

H (z) = \frac{b_{0} + b_{1} z^{- 1} + b_{2} z^{- 2}}{1 + a_{1} z^{- 1} + a_{2} z^{- 2}} (16)

Ce type de filtre est qualifié de biquadratique car le numérateur et le dénominateur de la fonction de transfert sont du deuxième ordre.

Pour concevoir un filtre passe-bande biquadratique, nous utilisons la méthode de Conception d'un filtre par placement des zéros et des pôles.

On choisit deux pôles complexes conjugués dont la partie imaginaire est la pulsation de résonance souhaitée et la partie réelle un nombre réel r inférieur strictement à 1 (pour la stabilité) mais proche de 1 pour avoir un grand facteur de qualité. Les deux zéros sont 1 et -1 afin d'annuler le gain à la fréquence nulle et à la fréquence de Nyquist. Voici la fonction de transfert en Z :

H (z) = b_{0} \frac{(z - 1) (z + 1)}{(z - r e^{i Ω_{a}}) (z - r e^{- i Ω_{a}})} = b_{0} \frac{1 - z^{- 2}}{1 - 2 r cos (Ω_{a}) z^{- 1} + r^{2} z^{- 2}} (17)

La pulsation de résonance réduite est définie à partir de la fréquence de résonance f₀ et de la fréquence d'échantillonnage f_e par :

Ω_{a} = 2 π \frac{f_{0}}{f_{e}} (18)

Le gain maximal est maintenu égal à 1 en choisissant :

b_{0} = \frac{1 - r^{2}}{2} (19)

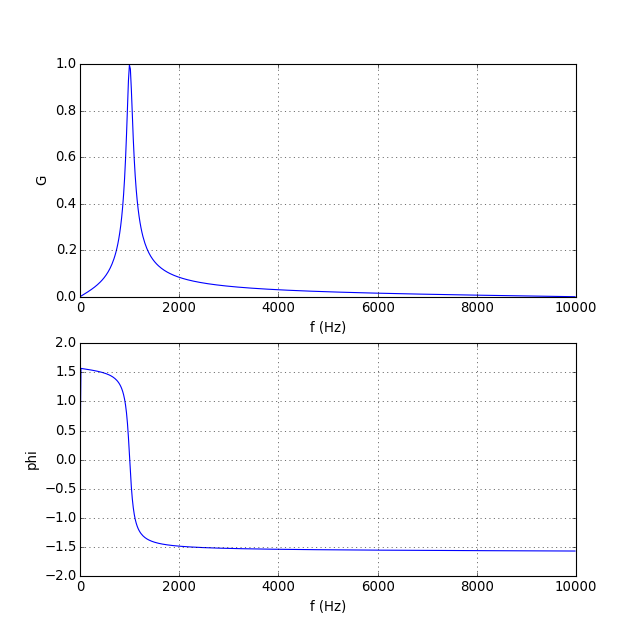
Considérons par exemple un filtre passe-bande de fréquence de résonance 1000  Hz pour une fréquence d'échantillonnage de 20  kHz :

import scipy.signal
fe=20000.0
fo=1000.0
omega_a=numpy.pi*fo/(fe/2)
r=0.98
b0=(1-r*r)*0.5
b=[b0,0,-b0]
a=[1,-2*r*numpy.cos(omega_a),r*r]
w,h =scipy.signal.freqz(b,a)
g = numpy.absolute(h)
phase = numpy.unwrap(numpy.angle(h))
figure(figsize=(8,8))
subplot(211)
plot(w/(2*numpy.pi)*fe,g)
xlabel("f (Hz)")
ylabel("G")
grid()
subplot(212)
plot(w/(2*numpy.pi)*fe,phase)
xlabel("f (Hz)")
ylabel("phi")
grid()

figF.pdf

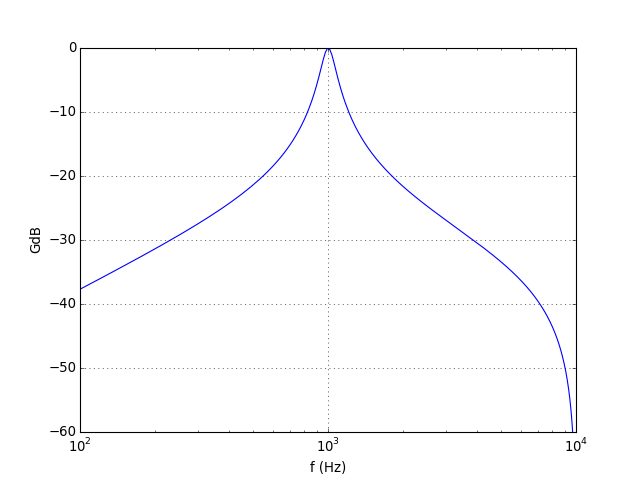
Voici le diagramme de Bode dans la bande [100,10000]  Hz :

figure()
plot(w/(2*numpy.pi)*fe,20*numpy.log10(g))
xlabel('f (Hz)')
ylabel("GdB")
xscale('log')
axis([100,10000,-60,0])
grid()

figG.pdf

3.b. Réponse impulsionnelle

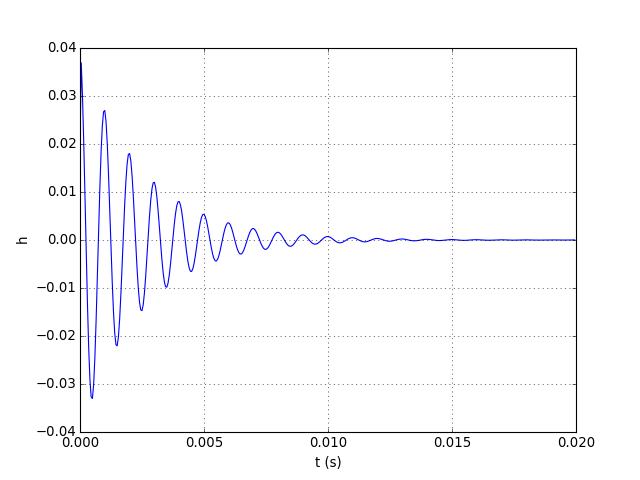
La réponse impulsionnelle d'un filtre numérique est obtenue facilement par le calcul avec une impulsion unité en entrée, c'est-à-dire x₀=1 et x_n=0 pour n>0.

N=400
t=numpy.arange(N)*1.0/fe
y=numpy.zeros(N)
x=numpy.zeros(N)
x[0]=1
y[0]=b[0]*x[0]
y[1]=b[0]*x[1]+b[1]*x[0]-a[1]*y[0]
y[2]=b[0]*x[2]+b[1]*x[1]+b[2]*x[0]-a[1]*y[1]-a[2]*y[0]
for n in range(3,N):
    y[n] = b[0]*x[n]+b[1]*x[n-1]+b[0]*x[n-2]-a[1]*y[n-1]-a[2]*y[n-2]

figure()
plot(t,y)
xlabel("t (s)")
ylabel("h")
grid()

figH.pdf

Le coefficient r (partie réelle des pôles) contrôle le facteur de qualité, qui augmente lorsque r s'approche de 1. Une comparaison rapide de la réponse impulsionnelle avec celle du filtre analogique (déterminée expérimentalement plus haut) permet d'ajuster le coefficient r pour obtenir un filtre similaire au filtre analogique.

3.c. Filtrage d'un signal

La carte d'acquisition Sysam SP5 est utilisée pour numériser le signal délivré par un GBF. La fonction config_filtre permet de réaliser un filtrage pendant l'acquisition. Une acquisition en mode permanent est réalisée, ce qui permet de programmer une animation pour visualiser les deux signaux en temps réel. Le script suivant réalise cela. La difficulté est de réaliser une synchronisation de l'affichage par rapport au signal. Une synchronisation logicielle (en python) a été ajoutée, imparfaite mais suffisante pour une observation confortable des signaux. La fenêtre d'affichage comporte aussi deux curseurs pour régler la fréquence de résonance et le coefficient r en temps réel. La possibilité d'ajuster très facilement les paramètres du filtre est bien sûr un avantage important du filtre numérique par rapport au filtre analogique.

acquisitionFiltragePasseBandeBiquad.py

import pycanum.main as pycan
import math
from matplotlib.pyplot import *
import matplotlib.animation as animation
import numpy
import scipy.signal
import time
import cmath


sys=pycan.Sysam("SP5")
Umax = 10.0
sys.config_entrees([0],[Umax])
fe=20000.0 # fréquence de la numérisation
te=1.0/fe
N = 100 # nombre d'échantillons dans la liste circulaire (fenêtre d'analyse)
duree = N*te
print(u"Durée de la fenêtre = %f s"%(duree))
sys.config_echantillon_permanent(te*1e6,N)
reduction = 1 # réduction de la fréquence d'échantillonnage après filtrage
fe_r = fe/reduction
te_r = te*reduction
longueur_bloc = int(N/reduction)


#filtre passe-bande
fo=1000.0
omega_a=numpy.pi*fo/(fe/2)
r=0.98
b0=(1-r*r)*0.5
b=[b0,0,-b0]
a=[1,-2*r*numpy.cos(omega_a),r*r]
w,h =scipy.signal.freqz(b,a)
g = numpy.absolute(h)
phase = numpy.unwrap(numpy.angle(h))
figure()
plot(w/(2*math.pi)*fe,g)
xlabel("f (Hz)")
ylabel("G")
grid()
figure()
plot(w/(2*math.pi)*fe,phase)
xlabel("f (Hz)")
ylabel("phi")
grid()
show() # tracé de la réponse fréquentielle du filtre
sys.config_filtre(a,b)

sys.lancer_permanent(repetition=1) # lancement d'une acquisition sans fin

fig0,ax0 = subplots()
subplots_adjust(left=0.1, bottom=0.3)
t = numpy.arange(longueur_bloc)*te_r
u = numpy.zeros(longueur_bloc)
line0, = ax0.plot(t,u,'r')
line1, = ax0.plot(t,u,'b')
yticks(numpy.linspace(-10,10,21))
ax0.grid()
ax0.axis([0,duree*0.5,-Umax,Umax])
ax0.set_xlabel("t (s)")
fo = 1000
slider_fo = Slider(axes([0.1,0.15,0.8,0.03]),"f0",100,2000,valinit=fo)
def update_fo(va):
    global fo,fe,sys,r,a,b
    fo = slider_fo.val
    omega_a=numpy.pi*fo/(fe/2)
    a=[1,-2*r*numpy.cos(omega_a),r*r]
    sys.config_filtre(a,b)
slider_fo.on_changed(update_fo)
slider_r = Slider(axes([0.1,0.05,0.8,0.03]),"r",0.9,0.999,valinit=r,valfmt='%1.3f')
def update_r(val):
    global fo,fe,sys,r,a,b
    r = slider_r.val
    b0=(1-r*r)*0.5
    b=[b0,0,-b0]
    a=[1,-2*r*numpy.cos(omega_a),r*r]
    sys.config_filtre(a,b)
slider_r.on_changed(update_r)

def animate0(i): # tracé du signal
    global sys,line0,data,u,t
    data = sys.paquet(-1,reduction)
    if data.size!=0:
        u1=data[1]
        u2=data[2]
        i=0
        while u1[i]<0:
            i+=1
        while u1[i]>0:
            i+=1
        ta=t[i:N-1]
        ta=ta-ta[0]
        line0.set_ydata(u1[i:N-1])
        line0.set_xdata(ta)
        line1.set_ydata(u2[i:N-1])
        line1.set_xdata(ta)


ani0 = animation.FuncAnimation(fig0,animate0,frames=100,repeat=True,interval=duree*1000)

show(block=True)
sys.stopper_acquisition()
time.sleep(1)
sys.fermer()