Mesure d'une impédance
1. Introduction
Cette page montre comment utiliser la carte d'acquisition SysamSP5 pour faire les mesures d'impédance en fonction de la fréquence. On verra en particulier une méthode de traitement du signal permettant de déterminer le déphasage entre le courant et la tension. Les techniques utilisées peuvent se généraliser à l'étude de la réponse fréquentielle d'un circuit linéaire.
2. Dispositif expérimental
Le dispositif permet d'imposer à l'impédance Z étudiée une tension U sinusoïdale au moyen d'un générateur de fonctions basse fréquence (GBF). Un convertisseur courant-tension permet de mesurer le courant en fournissant la tension -RI. La résistance de ce convertisseur est ici R=100 Ω, mais on pourra l'augmenter pour les très fortes impédances. Les deux ampli-op qui alimentent l'impédance Z limitent le courant à environ 20 mA. L'acquisition des signaux U et -RI se fait avec une carte SysamSP5, dont l'alimentation -12/0/+12 V est utilisée pour alimenter le quadruple ampli-op JFET TL074.
Figure pleine pageLorsque l'impédance est faible, l'amplitude de la tension délivrée par le GBF doit être faible, ce qui peut amener à utiliser l'atténuateur -20 dB ou -40 dB. On contrôle les tensions U et -RI à l'oscilloscope pour vérifier le fonctionnement linéaire. Pour les fortes impédances, on peut être amené à augmenter la résistance R car le courant est très faible. Le suiveur permet alors à la carte de lire la tension U en prélevant un courant infime dans le circuit de l'impédance.
3. Traitement des signaux
3.a. Rapport des amplitudes
On dispose de deux signaux sinusoïdaux e(t) et s(t). Dans le cas présent, e(t)=U(t) et s(t)=i(t). D'une manière plus générale, e(t) et s(t) sont les signaux d'entrée et de sortie d'un système linéaire, par exemple un filtre.
La première grandeur à extraire est le rapport des amplitudes de ces deux signaux, qui dans le cas présent nous donne le module de l'impédance.
Soit la valeur moyenne du signal e(t). On considère la valeur efficace suivante :
Pour un signal sinusoïdal (avec une éventuelle composante continue), si E est l'amplitude des oscillations, on a :
Soit en le signal numérisé à la fréquence d'échantillonage Te. Une valeur approchée de la valeur efficace est obtenue avec N échantillons de la manière suivante :
Il s'agit de l'écart-type, qui peut être calculé avec la fonction numpy.std.
La rapport d'amplitude recherché est :
3.b. Déphasage
Il s'agit de déterminer le déphasage entre les deux signaux sinusoïdaux s(t) et e(t), à partir des signaux échantillonnés en et sn. On remarque tout d'abord que la précision de cette mesure ne peut être meilleure que :
Il faut donc échantillonner à une fréquence largement supérieure à la fréquence de Nyquist, par exemple 100 échantillons par période pour avoir une précision de 1 pour cent. La mesure d'un déphasage est donc particulièrement exigeante en fréquence d'échantillonnage (ce n'est pas le cas de l'amplitude).
Considérons deux signaux de valeur moyenne nulle, qui s'écrivent :
Le produit de ces deux fonctions s'écrit :
Sa valeur moyenne est donc :
Connaissant les valeurs efficaces, on peut donc calculer . La fonction arccos permet en principe d'en déduire le déphasage. Cependant, l'incertitude du déphasage serait :
L'incertitude est très grande lorsque est faible. Pour déterminer plus précisément un déphasage faible, on introduit une fonction e'(t) en quadrature avec e(t) :
La moyenne du produit avec s(t) est :
Cette relation nous permet d'obtenir des déphasages petits. Il faut cependant disposer d'un signal e'(t). L'idéal serait d'avoir un signal analogique e'(t) dérivé de e(t). Ce n'est pas le cas ici, donc on doit obtenir ce signal en quadrature numériquement. Pour cela, il faut obtenir tout d'abord la période du signal. Il suffit de déterminer le spectre en fréquence de en avec sa transformée de Fourier discrète et de déterminer l'indice Pm correspondant à la valeur maximale de la première moitié du spectre. Cet indice est celui de la fréquence, soit :
On en déduit le décalage d'indice à appliquer sur le signal pour obtenir un déphasage de π/2 :
Il faut bien sûr calculer la valeur entière de ce décalage.
3.c. Fonction de corrélation
Une autre manière d'obtenir le déphasage est de calculer la fonction de corrélation entre les deux signaux.
Pour deux fonctions f(t) et g(t), le produit de convolution est défini par :
La transformée de Fourier d'un produit de convolution est le produit des transformées de Fourier des deux fonctions (théorème de convolution) :
La fonction de corrélation croisée des deux signaux est définie par :
La transformée de Fourier de la fonction de corrélation est le produit de la transformée de Fourier de l'une des fonctions par le conjugué de la transformée de Fourier de la seconde :
Pour un signal échantillonné, on calcule la fonction de corrélation en faisant ce produit des transformées de Fourier discrètes suivi d'une transformée de Fourier discrète inverse.
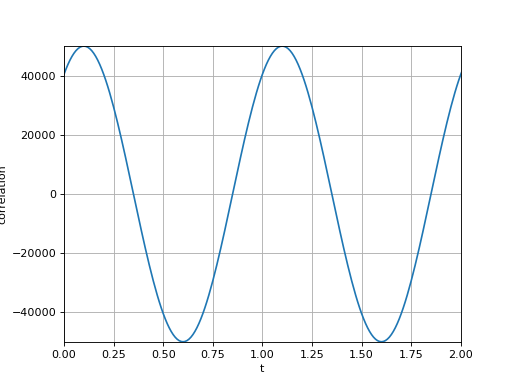
Voici un exemple avec deux signaux sinusoïdaux (de période 1) déphasés d'un dixième de période. Un décalage est introduit sur le second signal.
import numpy
import numpy.fft
from matplotlib.pyplot import *
T = 1000.0
N = 100000
te = T/N
t = numpy.arange(N)*te
f = numpy.cos(2*numpy.pi*t)
g = numpy.cos(2*numpy.pi*(t+0.1))+0.1
tfd_f = numpy.fft.fft(f)
tfd_g = numpy.fft.fft(g)
cor = numpy.fft.ifft(numpy.conjugate(tfd_g)*tfd_f)
figure()
plot(t,cor)
xlabel("t")
ylabel("correlation")
axis([0,2,cor.min(),cor.max()])
grid()
 figA.pdf
figA.pdf
La fonction de corrélation est périodique, de période T. L'instant du premier maximum permet de calculer le déphasage. Soit k l'indice du maximum de la corrélation dans l'intervalle [0,T] et q le nombre d'échantillons pour une période T (calculé à partir de la TFD comme expliqué plus haut). Le déphasage de g par rapport à f est :
La valeur obtenue est dans l'intervalle [0,2π].
Voici le calcul du décalage temporel pour l'exemple précédent :
P = int(1.0/te)
k = numpy.argmax(cor[0:P]) # premier max
tau = k*1.0/P
print(tau) --> 0.1
En appliquant le produit des TFD dans l'autre sens, on obtient le déphasage de f par rapport à g.
4. Programme d'acquisition
Le script python ci-dessous effectue les acquisitions et le calcul de l'impédance. Pour chaque point, l'utilisateur doit entrer la fréquence approximative (lue sur le GBF). La fréquence d'échantillonnage est calculée, avec si possible 100 points par période, ce qui doit donner une précision de 1 pour cent sur le déphasage. La durée d'une acquisition de N échantillons est de 1 seconde (si possible), ce qui garantit une précision de 1 Hertz pour la détermination de la fréquence.
L'acquisition et le calcul de l'impédance sont faits dans la fonction mesure(a0,a1,f,plt). a0,a1 sont les calibres des voies 0 et 1, f et la fréquence approximative, et plt est un booléen qui indique s'il faut tracer les signaux.
Les traitements effectuées par cette fonction sont :
- Numérisation de U(t) et RI(t) avec 100 points par période sur une durée de 1 seconde (si possible).
- Calcul des écart-types et du module de l'impédance.
- Calcul des transformées de Fourier discrètes.
- Calcul de la fréquence et du nombre d'échantillons pour la période.
- Calcul du déphasage par la multiplication des signaux.
- Calcul du déphasage par la fonction de corrélation.
- Renvoi des amplitudes (approximatives), de la fréquence, du module de l'impédance, des deux déphasages et de l'incertitude sur le déphasage.
Pour chaque mesure, la fonction précédente est appelée deux fois. La première fois, les calibres maximals sont utilisés (10 V) ce qui permet d'obtenir la valeur des amplitudes des deux tensions U et RI. Le second appel se fait avec ces amplitudes, ce qui permet de choisir le calibre de l'amplificateur au mieux. Lorsque l'impédance est élevée, le courant est faible et il faut donc un gain important sur la voie EA1. Inversement, il faut un gain important sur la voie EA0 lorsque l'impédance est faible.
Les signaux sont tracés lors du second appel. On peut alors vérifier qu'ils sont bien sinusoïdaux (une vérification à l'oscilloscope est faite en parallèle). Pour plus de précision, on peut ajouter un tracé des spectres afin de vérifier le taux de distorsion.
La boucle principale du programme consiste à remplir des listes. Pour chaque impédance à mesurer, l'utilisateur entre la fréquence approximative (ou bien N lorsqu'il a terminé les mesures). Les données sont enregistrées dans un fichier texte.
# -*- coding: utf-8 -*-
import pycan.main as pycan
import numpy
import numpy.fft
from matplotlib.pyplot import *
sys = pycan.Sysam("SP5")
R = 100.0 # convertisseur courant-tension
def mesure(a0,a1,f,plt):
global sys,R
sys.config_entrees([0,1],[a0,a1])
fe = f*100
if fe > 1.0e7:
fe = 1.0e7
te = 1.0/fe
T = 1.0
ne = int(T/te)
if ne > 120000:
ne = 120000
print("fe = %f"%fe)
T = ne*te
print("T = %f"%T)
sys.config_echantillon(te*1e6,ne)
sys.acquerir()
u=sys.entrees()
t=sys.temps()[0]
te = t[1]-t[0]
U = u[0]
RI = -u[1]
U = u-U.mean()
RI = RI-RI.mean()
tfd_U = numpy.fft.fft(U)
tfd_RI = numpy.fft.fft(RI)
spectre = numpy.absolute(tfd_U)
correlation = numpy.fft.ifft(numpy.conjugate(tfd_U)*tfd_RI)
freq = numpy.argmax(spectre[0:int(ne/2)])*1.0/(te*ne)
periode = 1.0/freq
p = int(periode/te/4) # decalage quadrature
V = numpy.roll(U,p,0)
cos = numpy.mean(U*RI)
sin = numpy.mean(V*RI)
norme = numpy.sqrt(cos**2+sin**2)
cos = cos/norme
sin = sin/norme
Ueff = numpy.std(U)
RIeff = numpy.std(RI)
#A = Ueff*RIeff
#cos = cos/A
#sin = sin/A
print("Frequence = %f"%freq)
Z = Ueff/RIeff*R
phi = numpy.angle(cos+sin*1j)
incert = te*f*numpy.pi*2
print("Z = %f, cos = %f, sin = %f, phi = %f, incert = %f"%(Z,cos,sin,phi,incert))
# methode par correlation
q = int(periode/te)
k = numpy.argmax(correlation[0:q])
theta = k*1.0/q*2*numpy.pi
print("theta = %f"%theta)
if plt:
figure()
plot(t,U)
xlabel("t (s)")
ylabel("U (V)")
axis([0,10.0/f,-a0,a0])
grid()
figure()
plot(t,RI)
xlabel("t (s)")
ylabel("RI (V)")
axis([0,10.0/f,-a1,a1])
grid()
show(block=True)
return (numpy.std(U)*1.6,numpy.std(RI)*1.6,freq,Z,phi,theta,incert)
liste_freq = []
liste_Z = []
liste_phi = []
liste_theta = []
liste_incert = []
while True:
r = raw_input("Frequence approximative (Hz) (taper N pour finir) ?")
if r=="N":
break
f = float(r)
(a0,a1,freq,Z,phi,theta,incert) = mesure(10,10,f,plt=False)
(a0,a1,freq,Z,phi,theta,incert) = mesure(a0,a1,f,plt=True)
liste_freq.append(freq)
liste_Z.append(Z)
liste_phi.append(phi)
liste_theta.append(theta)
liste_incert.append(incert)
sys.fermer()
numpy.savetxt("impedance-1.txt",[liste_freq,liste_Z,liste_phi,liste_theta,liste_incert])
figure()
plot(liste_freq,liste_Z,'o')
xlabel("f (Hz)")
ylabel("Z (Ohm)")
grid()
figure()
plot(liste_freq,liste_phi,'o')
plot(liste_freq,liste_theta,'o')
xlabel("f (Hz)")
ylabel("phi (rad)")
grid()
show(block=True)
5. Exemple : impédance d'une bobine
Lorsque la fréquence est grande, l'impédance d'une bobine est grande et donc le courant est faible. Un éventuel décalage de tension en entrée conduit alors à un décalage relatif grand en sortie, ce qui est gênant pour l'utilisation de l'amplificateur de la carte d'acquisition. Pour éviter cet inconvénient, on ajoute un filtre RC passe-haut (couplage AC) à la sortie du convertisseur courant-tension, avec C=1 μF et R=1 MΩ, ce qui donne une coupure en dessous de 0,16 Hz.
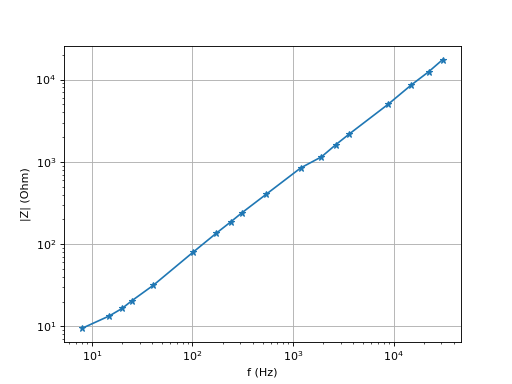
Voici un premier exemple avec une bobine à cadre en ferrite (la moitié d'une double bobine), d'inductance 100 mH.

data = numpy.loadtxt("impedance-100mH.txt")
f = data[0]
Z = data[1]
phi = data[2]
theta = data[3]
epsilon = data[4]
Voici le tracé du module de l'impédance :
figure()
plot(f,Z,"*-")
xlabel("f (Hz)")
ylabel("|Z| (Ohm)")
xscale("log")
yscale("log")
grid()
 figB.pdf
figB.pdf
On voit bien le domaine de fréquence où l'auto-inductance domine. Une régression linéaire sur les derniers points permet d'obtenir l'auto-inductance approximative, car Z=2πLf à haute fréquence :
from scipy import stats
(i1,i2) = (-7,-1)
a,b,r_value,p_value,std_err = stats.linregress(f[i1:i2],Z[i1:i2])
L = a/(2*numpy.pi)
print(L) --> 0.08795589867922761
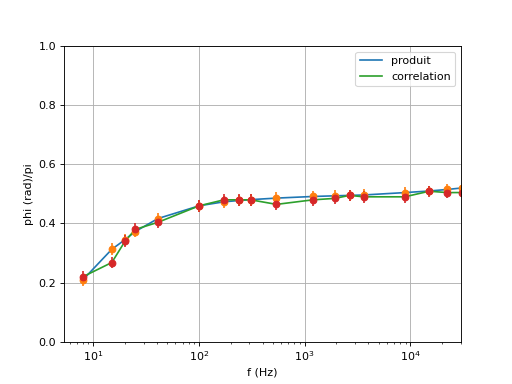
Voici le tracé des déphasages obtenus par les deux méthodes (la fréquence est en échelle log) :
figure()
plot(f,phi/numpy.pi,"-",label="produit")
errorbar(f,phi/numpy.pi,yerr=epsilon/numpy.pi,fmt='o')
plot(f,theta/numpy.pi,"-",label="correlation")
errorbar(f,theta/numpy.pi,yerr=epsilon/numpy.pi,fmt='o')
xlabel("f (Hz)")
xscale("log")
ylabel("phi (rad)/pi")
axis([0,30000,0,1])
legend(loc="upper right")
grid()
 figC.pdf
figC.pdf
Le déphasage tend vers π/2 à haute fréquence. On remarque que pour la plus haute fréquence (30 kHz), il y a bien 100 échantillons par période (échantillonnage à 3 MHz), ce qui garantit une bonne précision sur le déphasage.
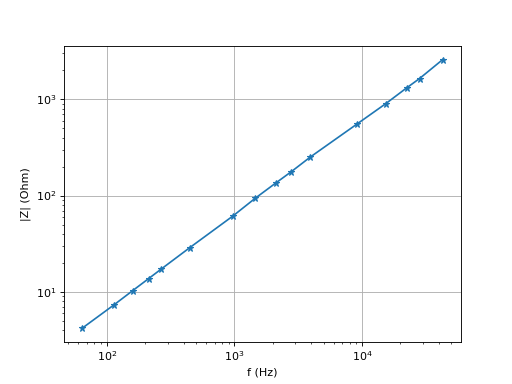
Voici une bobine de même type de 10 mH :
data = numpy.loadtxt("impedance-10mH.txt")
f = data[0]
Z = data[1]
phi = data[2]
theta = data[3]
epsilon = data[4]
figure()
plot(f,Z,"*-")
xlabel("f (Hz)")
ylabel("|Z| (Ohm)")
xscale("log")
yscale("log")
grid()
 figD.pdf
figD.pdf
a,b,r_value,p_value,std_err = stats.linregress(f,Z)
L = a/(2*numpy.pi)
print(L) --> 0.009435616876296028
figure()
plot(f,phi/numpy.pi,"-",label="produit")
errorbar(f,phi/numpy.pi,yerr=epsilon/numpy.pi,fmt='o')
plot(f,theta/numpy.pi,"-",label="correlation")
errorbar(f,theta/numpy.pi,yerr=epsilon/numpy.pi,fmt='o')
xlabel("f (Hz)")
xscale("log")
ylabel("phi (rad)/pi")
axis([0,f.max(),0,1])
legend(loc="upper right")
grid()
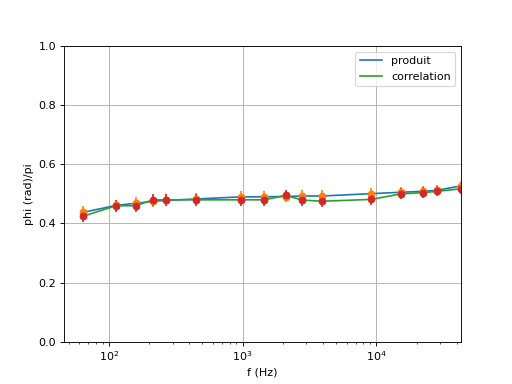 figE.pdf
figE.pdf
Voici les résultats obtenus avec une bobine fabriquée sur mesure, en enroulant 5 spires sur un noyau torique en ferrite.

data = numpy.loadtxt("impedance-191uH.txt")
f = data[0]
Z = data[1]
phi = data[2]
theta = data[3]
epsilon = data[4]
figure()
plot(f,Z,"*-")
xlabel("f (Hz)")
ylabel("|Z| (Ohm)")
xscale("log")
yscale("log")
grid()
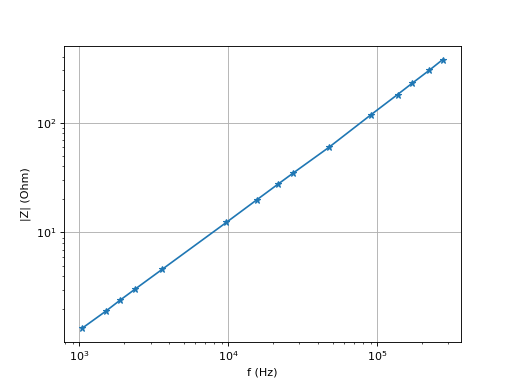 figF.pdf
figF.pdf
a,b,r_value,p_value,std_err = stats.linregress(f,Z)
L = a/(2*numpy.pi)
print(L) --> 0.00021569618712120013
figure()
plot(f,phi/numpy.pi,"-",label="produit")
errorbar(f,phi/numpy.pi,yerr=epsilon/numpy.pi,fmt='o')
plot(f,theta/numpy.pi,"-",label="correlation")
errorbar(f,theta/numpy.pi,yerr=epsilon/numpy.pi,fmt='o')
xlabel("f (Hz)")
xscale("log")
ylabel("phi (rad)/pi")
axis([0,f.max(),0,1])
legend(loc="upper right")
grid()
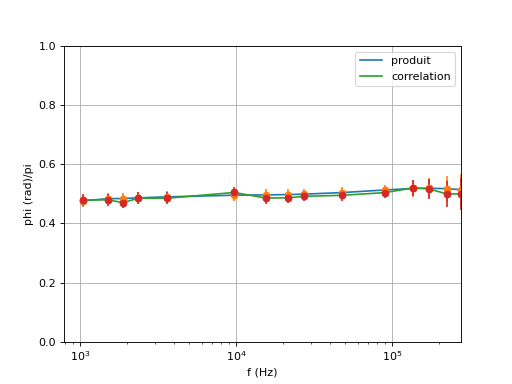 figG.pdf
figG.pdf
Pour les fréquences les plus élevées, l'incertitude sur le déphasage augmente car la fréquence d'échantillonnage maximale (10 MHz) ne permet pas d'obtenir 100 échantillons par période. Par exemple à f=200 kHz, il n'y a plus que 50 échantillons par période.