Filtres à réponse impulsionnelle finie

2.a. Définition

Un système linéaire causal à réponse impulsionnelle finie calcule une suite y_n à partir de la suite x_n par la relation :

$$y_n=\sum _{k=0}^{N-1}{h}_k{x}_{n-k}\text{(6)}$$

où les N coefficients h_k sont des constantes réelles. La valeur du signal discret y_n à l'instant n est donc obtenue par une combinaison linéaire des N valeurs précédentes du signal x_n. Ce système est dit causal car l'état de la sortie ne dépend que des états antérieurs de l'entrée.

On appelle impulsion un signal discret défini par :

$$\begin{array}{ccc}\hfill & x_0=1\hfill & \hfill \text{(7)}\\ \hfill & x_n=0sin\ne 0\hfill & \hfill \text{(8)}\end{array}$$

Pour une impulsion en entrée, le système linéaire fournit en sortie le signal :

$$y_n=h_n\text{(9)}$$

C'est pourquoi la suite h_n est appelée la réponse impulsionnelle (discrète) du système. La réponse impulsionnelle est ici finie puisqu'elle comporte N valeurs.

On remarque que le signal de sortie est le produit de convolution du signal d'entrée par la réponse impulsionnelle.

2.b. Fonction de transfert en Z

Ce système constitue un filtre à réponse impulsionnelle finie (filtre RIF). Considérons alors la transformée en Z du signal de sortie :

$$\begin{array}{ccc}\hfill Y\left(Z\right)& =\sum _{n=-\infty }^{n=+\infty }\sum _{k=0}^{N-1}{h}_k{x}_{n-k}{Z}^{-n}\hfill & \hfill \text{(10)}\\ \hfill & =\sum _{n\text{'}=-\infty }^{n\text{'}=+\infty }\sum _{k=0}^{N-1}{h}_k{x}_{n\text{'}}{Z}^{-n\text{'}}{Z}^{-k}\hfill & \hfill \text{(11)}\\ \hfill & =\left(\sum _{k=0}^{N-1}{h}_k{Z}^{-k}\right)\sum _{n\text{'}=-\infty }^{n\text{'}=+\infty }{x}_{n\text{'}}{Z}^{-n\text{'}}\hfill & \hfill \text{(12)}\\ \hfill & =H\left(Z\right)X\left(Z\right)\hfill & \hfill \text{(13)}\end{array}$$

où H(Z) est la fonction de transfert en Z définie par :

$$H\left(Z\right)=\sum _{k=0}^{N-1}{h}_k{Z}^{-k}\text{(14)}$$

2.c. Réponse fréquentielle

La réponse fréquentielle du filtre est obtenue en remplaçant Z par l'expression (4) :

$$H\left(f\right)=\sum _{k=0}^{N-1}{h}_{k}exp(-i2\pi kf{T}_e)\text{(15)}$$

On remarque que cette réponse fréquentielle ne dépend que de fT_e, qui est le rapport de la fréquence du signal sinusoïdal sur la fréquence d'échantillonnage. D'après le théorème de Shannon, ce rapport doit être inférieur à 1/2.

En remarquant que la réponse fréquentielle est de périodicité f_e=1/T_e (la fréquence d'échantillonnage), considérons les N fréquences suivantes :

$$f_n=\frac{n}{N{T}_e}\text{(16)}$$

On a alors

$$H\left(f_n\right)=\sum _{k=0}^{N-1}{h}_{k}exp(-i2\pi k\frac{n}{N})\text{(17)}$$

qui est (à un facteur N près) la transformée de Fourier discrète de la réponse impulsionnelle.

2.d. Exemple

Considérons comme exemple simple un filtre qui réalise la moyenne arithmétique de deux valeurs consécutives de l'entrée :

$$y_n=\frac{1}{2}(x_n+x_{n-1})\text{(18)}$$

Sa fonction de transfert en Z est :

$$H\left(Z\right)=\frac{1}{2}(1+Z^{-1})\text{(19)}$$

Voyons comment tracer sa réponse fréquentielle avec Mathematica :

H[Z_]:=0.5*(1+Z^(-1));
Hf[f_]:=H[Exp[I*2*Pi*f]];
                

Plot[Abs[Hf[f]],{f,0,0.5},PlotRange->{{0,0.5},{0,1}},AxesLabel->{"f/fe","|H|"}]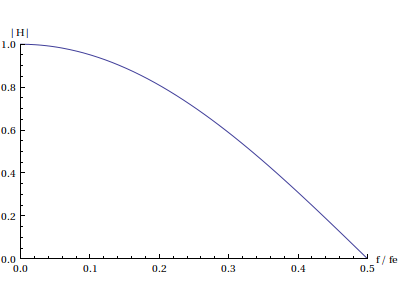

plotA.pdf

Plot[Arg[Hf[f]],{f,0,0.5},PlotRange->{{0,0.5},{-Pi,Pi}},AxesLabel->{"f/fe","phi"}]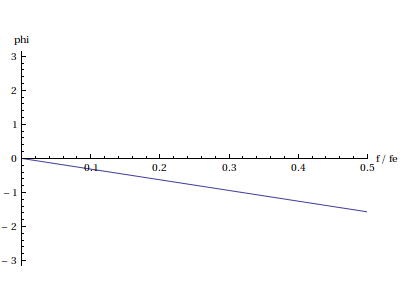

plotB.pdf

Le filtre moyenneur est un filtre passe-bas (assez peu sélectif). Le déphasage varie linéairement avec la fréquence. Cela se vérifie sur l'expression suivante de la réponse fréquentielle :

$$H\left(f\right)=cos\left(\pi f{T}_e\right)exp(-i\pi f{T}_e)\text{(20)}$$

Pour simuler l'action de ce filtre sur un signal, considérons le signal continu suivant et son échantillonnage :

x[t_]:=Cos[2*Pi*t]+0.05*Random[];
tmax=5;
n=1000;
tn=Table[(k-1)*tmax/n,{k,n}];
xn=Table[x[tn[[k]]],{k,n}];
                

ListPlot[Transpose[{tn,xn}],Joined->True,AxesLabel->{"t","x"}]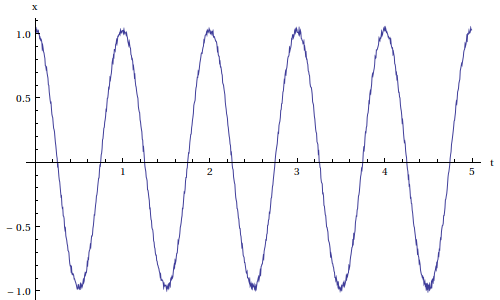

plotC.pdf

Pour obtenir le signal discret filtré, il suffit d'effectuer la convolution avec la réponse impulsionnelle. Le premier point calculé correspond à l'instant T_e, c'est pourquoi l'échelle de temps doit être modifiée.

h={0.5,0.5};
yn=ListConvolve[h,xn];
tn=Table[k*tmax/n,{k,n-1}];
                

ListPlot[Transpose[{tn,yn}],Joined->True,AxesLabel->{"t","y"}]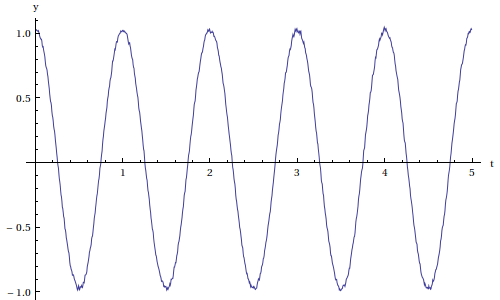

plotD.pdf

3.a. Définition et propriétés

Pour un filtre à phase linéaire, le déphasage est une fonction linéaire de la fréquence. La réponse fréquentielle a donc la forme suivante :

$$\begin{array}{ccc}\hfill & H\left(f\right)=G\left(f\right)exp(-i\phi \left(f\right))\hfill & \hfill \text{(21)}\\ \hfill & \phi \left(f\right)=2\pi f\tau \hfill & \hfill \text{(22)}\end{array}$$

La phase d'une composante de fréquence f devient en sortie du filtre :

$$2\pi ft-\phi \left(f\right)=2\pi f(t-\tau )\text{(23)}$$

Toutes les fréquences du signal subissent le même décalage τ en traversant le filtre. τ est le temps de propagation. Si toutes les composantes spectrales sont dans la bande passante, pour laquelle G(f)=1, on obtient :

$$y\left(t\right)=x(t-\tau )\text{(24)}$$

La forme du signal n'est pas modifiée par le filtrage en bande passante. Si on pose P=f_eτ (P entier), la fonction de transfert en Z d'un filtre à phase linéaire dans la bande passante est donc :

$$H_{bp}\left(Z\right)=Z^{-P}\text{(25)}$$

En isolant le terme contenant la phase, la réponse fréquentielle s'écrit d'après l'expression(15) :

$$H\left(f\right)=exp(-i2\pi fP{T}_e)\sum _{k=0}^{N-1}{h}_{k}exp(-i2\pi (k-P)f{T}_e)\text{(26)}$$

Après un changement de variable dans la somme, on en déduit l'expression du gain :

$$G\left(f\right)=\sum _{k=-P}^{N-1-P}{h}_{k+P}exp(-i2\pi kf{T}_e)\text{(27)}$$

On veut que G(f) soit réel. Il faut donc que la réponse impulsionnelle soit symétrique par rapport à l'indice P, c'est-à-dire :

$$h_{k+P}=h_{-k+P}\text{(28)}$$

On en déduit que N=2P+1. N est donc impair. Il est toutefois possible d'obtenir un filtre RIF à phase linéaire avec N pair en posant $P-\frac{1}{2}=f_e\tau$.

3.b. Synthèse par série de Fourier

Soit la suite définie par :

$$g_k=h_{k+P}(-P\le k\le P)\text{(29)}$$

Elle vérifie la propriété g_-k=g_k. La réponse fréquentielle s'écrit

$$H\left(f\right)=exp(-i2\pi f\tau )\sum _{k=-P}^P{g}_{k}exp(-i2\pi kf{T}_e)=exp(-i2\pi f\tau )G\left(f\right)\text{(30)}$$

En considérant la limite $P\to \infty$, on obtient alors :

$$G\left(f\right)=\sum _{k=-\infty }^{+\infty }{g}_{k}exp(-i2\pi kf{T}_e)\text{(31)}$$

On obtient un filtre à phase linéaire mais à réponse impulsionnelle infini (impossible à réaliser). Cette expression a toutefois l'avantage de faire apparaître g_k comme les coefficients de Fourier de la fonction G(f), fonction de période f_e=1/T_e. On a ainsi :

$$g_k=\frac{1}{f_e}{\int }_0^{f_e}G\left(f\right)exp\left(i2\pi k\frac{f}{f_e}\right)df\text{(32)}$$

Puisque g_-k=g_k, ces coefficients sont réels et la fonction G(f) est paire.

Pour une fonction de gain G(f) souhaitée, on calcule les coefficients de Fourier g_k puis on tronque la série de Fourier à un rang P de manière à obtenir la réponse impulsionnelle finie définie par :

$$h_k=g_{k-P}\left(0\le k\le 2P\right)\text{(33)}$$

Cette méthode revient à appliquer un fenêtrage rectangulaire aux coefficients de Fourier. La fonction G(f) effectivement obtenue après troncature est donc le produit de convolution de la fonction souhaitée par la transformée de Fourier de la fenêtre. En pratique, il est préférable d'appliquer d'autres types de fenêtres, comme les fenêtres de Hanning ou Hamming.

3.c. Exemple : filtre RIF passe-bas

La fonction de gain souhaitée est définie sur l'intervalle [-f_e/2,f_e/2] par :

$$\begin{array}{ccc}\hfill G\left(f\right)& =1pour-f_c\le f\le f_c\hfill & \hfill \text{(34)}\\ \hfill & =0pour{f}_c<\left|f\right|\le \frac{f_e}{2}\hfill & \hfill \text{(35)}\end{array}$$

Les coefficients de Fourier de cette fonction sont :

$$g_k=\frac{1}{k\pi }sin\left(2\pi k\frac{f_c}{f_e}\right)\text{(36)}$$

Le résultat peut s'exprimer avec la fonction sinus cardinal et ne dépend que du rapport de la fréquence de coupure sur la fréquence d'échantillonnage $a=\frac{f_c}{f_e}$ :

$$g_k=2asinc\left(2\pi ka\right)\text{(37)}$$

Considérons le cas d'une troncature par une fenêtre rectangulaire au rang P. La fonction suivante calcule les coefficients h_k :

reponseImp[a_,p_]:=Table[2*a*Sinc[2*Pi*(k-p)*a],{k,0,2*p}];

Par exemple pour un filtre d'ordre N=21 (P=10) avec a=0.2, on obtient :

h=reponseImp[0.2,10];

La fonction suivante permet d'obtenir la réponse fréquentielle :

reponseFreq[h_,f_]:=Sum[h[[k]]*Exp[-I*2*Pi*k*f],{k,Length[h]}];

Voici le tracé du gain et de la phase du filtre :

Plot[Abs[reponseFreq[h,f]],{f,0,0.5},AxesLabel->{"f/fe","G"}]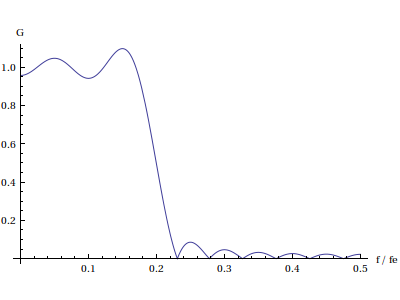

plotE.pdf

Plot[Arg[reponseFreq[h,f]],{f,0,0.5},AxesLabel->{"f/fe","phi"}]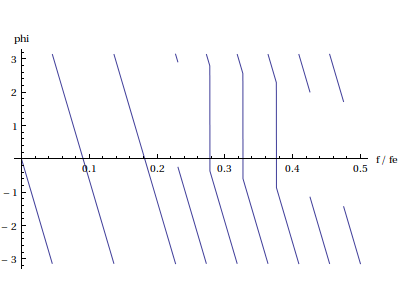

plotF.pdf

On constate que la phase est bien linéaire dans la bande passante, mais le gain présente des ondulations très fortes. Dans la bande atténuée, il y a des discontinuités de π de la phase. Bien sûr, les différences par rapport à la fonction de transfert souhaitée sont dûes à la troncature de la réponse impulsionnelle.

Essayons une troncature par une fenêtre de Hann :

reponseImp[a_,p_]:=Table[2*a*Sinc[2*Pi*(k-p)*a]*0.5*(1+Cos[(k-p)*2*Pi/(2*p+1)]),
                {k,0,2*p}];
p=10;
h=reponseImp[0.2,p];
                

Plot[Abs[reponseFreq[h,f]],{f,0,0.5},AxesLabel->{"f/fe","G"}]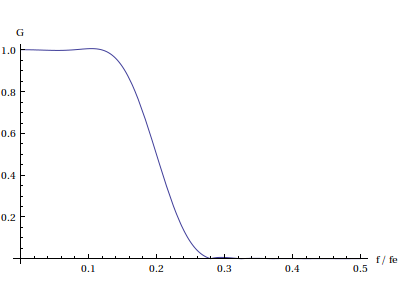

plotG.pdf

Plot[Arg[reponseFreq[h,f]],{f,0,0.5},AxesLabel->{"f/fe","phi"}]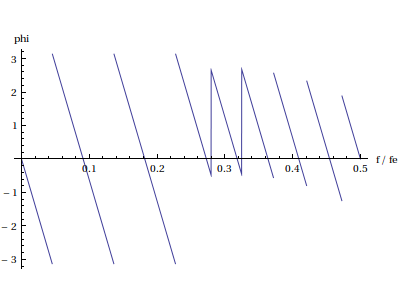

plotH.pdf

Les ondulations dans la bande passante et dans la bande atténuée sont considérablement réduites. La linéarité de la phase dans la bande passante est toujours assurée.

Lorsque ce filtre est utilisé dans un système de traitement du signal temps-réel, pour un signal situé dans la bande passante, la sortie présente un retard de τ=PT_e par rapport à l'entrée. Cela se comprend aisément en remarquant que le point prépondérant pour le calcul de y_n est x_n-P (terme g₀). Pour obtenir un filtre très sélectif, il faut augmenter P. Si le retard τ doit rester fixe, il faut parallèlement augmenter la fréquence d'échantillonnage.

Pour l'analyse de données expérimentales (échantillon fini), le retard τ n'a aucune signification physique et peut être annulé de la manière suivante. Soit Q le nombre de points de l'échantillon. Le premier point de la sortie calculé est y_2P puisqu'il faut au moins 2P+1 valeurs antérieures de x_n pour appliquer la convolution. Ce premier point est en retard de τ=PT_e par rapport à l'entrée. Annuler le retard revient donc à attribuer l'instant (2P-P)T_e=PT_e à ce premier point. Ainsi, le dernier point calculé y_Q-2P correspond à l'instant (Q-P)T_e. L'application du filtrage revient donc à enlever les P premiers instants et les P derniers instants de l'échantillon. Voyons cela sur un exemple.

On fait un échantillonnage d'un signal comportant du bruit :

x[t_]:=Cos[2*Pi*t]+0.1*Random[];
tmax=2;
n=200;
tnx=Table[(k-1)*tmax/n,{k,n}];
xn=Table[x[tnx[[k]]],{k,n}];
                

Le filtrage se fait avec la fonction de convolution :

yn=ListConvolve[h,xn];

Comparons les longueurs des deux listes :

{200, 180}

Comme prévu, la sortie a perdu 2P points par rapport à l'entrée. Pour ne pas avoir de décalage entre le signal filtré et le signal d'origine, l'échelle de temps du signal filtré est calculée comme suit :

tny=Table[tnx[[p+k]],{k,Length[yn]}];

On trace les deux signaux :

ListPlot[Transpose[{tnx,xn}],Joined->True,AxesLabel->{"t","x"}]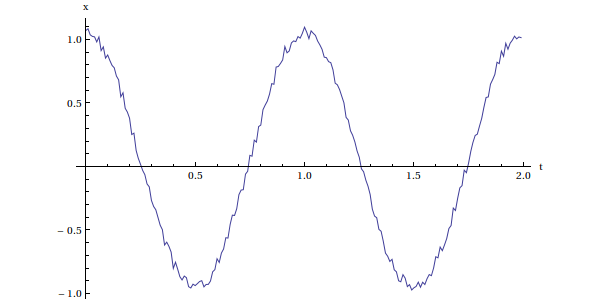

plotI.pdf

ListPlot[Transpose[{tny,yn}],Joined->True,AxesLabel->{"t","y"}]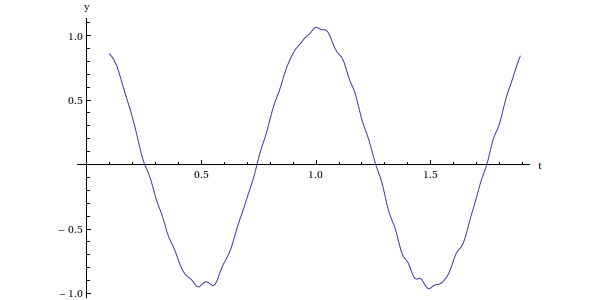

plotJ.pdf

Le signal traité est bien synchrone avec le signal d'origine; les P premiers et les P derniers points sont perdus. Dans un filtre numérique temps-réel, la sortie serait décalée de τ=PT_e vers la droite.