Calculs d'intégrales : méthode de Romberg

2.a. Méthode

On considère une fonction f de la variable réelle x dont on cherche à évaluer numériquement l'intégrale sur un intervalle fini [a;b] :

$$I={\int }_a^{b}f\left(x\right)dx\text{(1)}$$

La fonction f est supposée définie en tout point de l'intervalle [a;b].

Pour obtenir une approximation de cette intégrale, on considère une subdivision de l'intervalle [a;b] en N intervalles égaux, chacun de largeur h=(b-a)/N. Le nombre N est une puissance de 2. On pose donc :

$$\begin{array}{cc}\hfill & N=2^{p}p=0,1,2,\dots \hfill \\ \hfill & h_p=\frac{b-a}{N}\hfill \\ \hfill & x_0=a\hfill \\ \hfill & x_N=b\hfill \\ \hfill & x_k=x_0+khk=0,1,2,\dots N\hfill \end{array}$$

La figure suivante montre un exemple pour p=2 :

Figure pleine page

La formule des trapèzes consiste à approximer l'intégrale sur chaque intervalle par l'aire du trapèze :

$${\int }_{x_k}^{x_{k+1}}f\left(x\right)dx\simeq h{f}_k+h\frac{1}{2}(f_{k+1}-f_k)=h\frac{1}{2}(f_k+f_{k+1})\text{(2)}$$

On obtient ainsi une approximation de l'intégrale, pour un indice p :

$$I_p=h_p[\frac{1}{2}{f}_0+f_1+f_2+\dots +f_{N-2}+f_{N-1}+\frac{1}{2}{f}_N]=h_p{S}_p\text{(3)}$$

Mis à part le premier et le dernier terme, correspondant à x=a et x=b, il s'agit de calculer la somme des f_k.

Cette approximation de l'intégrale étant calculée, on obtient une meilleure approximation en divisant h par deux, c'est-à-dire en ajoutant les points milieux des intervalles. La figure suivante montre le passage de p=2 à p=3 :

Figure pleine page

On remarque que la somme S_p peut être réutilisée pour calculer S_p+1. Il suffit d'ajouter les points milieux, encadrés sur la figure.

Pour calculer une approximation de l'intégrale, on choisit une tolérance ε puis on procède par itérations. La première somme à calculer est :

$$S_0=\frac{1}{2}(f\left(a\right)+f\left(b\right))\text{(4)}$$

Connaissant la somme S_p, on calcule la somme S_p+1 en ajoutant la somme des f_k des points milieux. L'itération est stoppée lorsque la valeur absolue de la différence des deux évaluations consécutives de l'intégrale est inférieure à la tolérance :

$$|I_{p+1}-I_p|<\epsilon \text{(5)}$$

2.b. Implémentation

Les fonctions sont définies dans une classe :

      
class Romberg:
    def __init__(self,f,a,b):
        self.f = f
        self.a = a
        self.b = b
        self.p = 0
        self.N = 1
        self.S = 0.5*(f(a)+f(b))
        self.h = (b-a)
        self.I = self.S*self.h
        self.I_last = self.I
        self.n_eval = 0
    def iteration(self):
        self.n_eval += self.N
        x = self.a+self.h*0.5
        somme = self.f(x)
        for k in range(self.N-1):
            x += self.h
            somme += f(x)
        self.N *= 2
        self.p += 1
        self.S += somme
        self.h *= 0.5
        self.I_last = self.I
        self.I = self.h*self.S
        
    def iterations(self,P):
        I = [self.I]
        h = [self.h]
        while self.p<P:
            self.iteration()
            I.append(self.I)
            h.append(self.h)
        return (numpy.array(h),numpy.array(I))
        
    def trapezes(self,epsilon):
        I = [self.I]
        h = [self.h]
        self.iteration()
        while abs(self.I-self.I_last)>epsilon:
            self.iteration()
            I.append(self.I)
            h.append(self.h)
        return (numpy.array(h),numpy.array(I))
        
    def romberg(self,epsilon):
        jmax = 20
        A=numpy.zeros((jmax+1,jmax+1))
        A[0][0] = self.I
        self.iteration()
        A[1][0] = self.I
        correction = (A[1][0]-A[0][0])/3
        A[1][1] = A[1][0] + correction
        j = 2
        while abs(correction) > epsilon:
            self.iteration()
            A[j][0] = self.I
            for i in range(1,j+1):
                correction = (A[j][i-1]-A[j-1][i-1])/(4**i-1)
                A[j][i] = A[j][i-1] + correction
            j += 1
        return (A[0:j-1,0:j-1],A[j-1][j-1])
                    

Dans le constructeur, on fournit la fonction à intégrer et les bornes de l'intervalle. Les variables h,p,N sont initialisées. On calcule la première somme S, la première valeur de h, et la première estimation de l'intégrale I.

La fonction iteration() calcule la somme S_p+1 et met à jour les différentes variables, en particulier l'estimation self.I de l'intégrale.

La fonction iterations(P) effectue les itérations jusqu'à un rang P (pour le nombre p). Elle renvoie la liste des largeurs h et la liste des estimations successives de l'intégrale.

La fonction trapezes(epsilon) effectue les itérations pour une tolérance donnée. Elle renvoie la liste des largeurs h et la liste des estimations successives de l'intégrale.

Comme premier exemple, on considère l'intégrale suivante :

$${\int }_0^1{x}^{5}dx=\frac{1}{6}\text{(6)}$$

import numpy
def f(x):
    return x**5
romberg = Romberg(f,0,1)
(h,I) = romberg.trapezes(1e-7)
                    

Voici l'erreur :

print(I[-1]-1.0/6)
--> 2.4835268314093994e-08

et le nombre d'évaluations de la fonction f :

print(romberg.n_eval)
--> 4095

On trace l'erreur pour les différentes approximations de l'intégrale, en fonction du carré de h :

from matplotlib.pyplot import *
figure(figsize=(8,6))
plot(h*h,numpy.absolute(I-1.0/6),"o")
xlabel("$h^2$",fontsize=18)
ylabel("$e$",fontsize=18)
xscale('log')
yscale('log')
grid()
                    

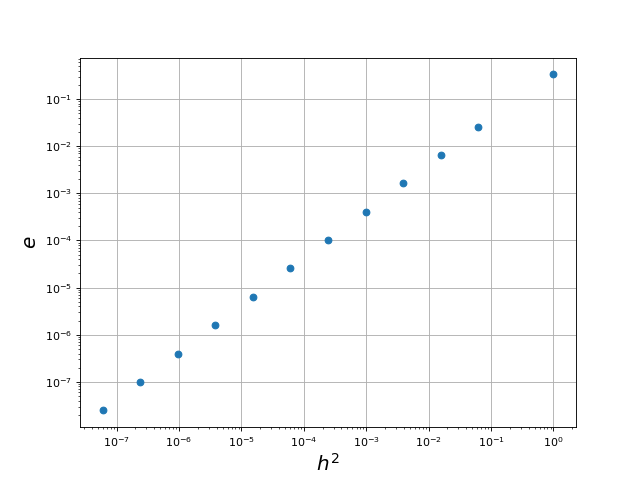figA.pdf

La pente égale à 1 montre que l'erreur est proportionnelle à h².

3.a. Principe

Considérons l'application de la méthode des trapèzes jusqu'au rang p, par exemple p=3, et traçons l'estimation de l'intégrale en fonction de h².

romberg = Romberg(f,0,1)
(h,I) = romberg.iterations(3)
figure(figsize=(8,6))
plot(h*h,I,"o")
xlabel("$h^2$",fontsize=18)
ylabel("$I$",fontsize=18)
axis([0,1.5,0,1])
grid()
                

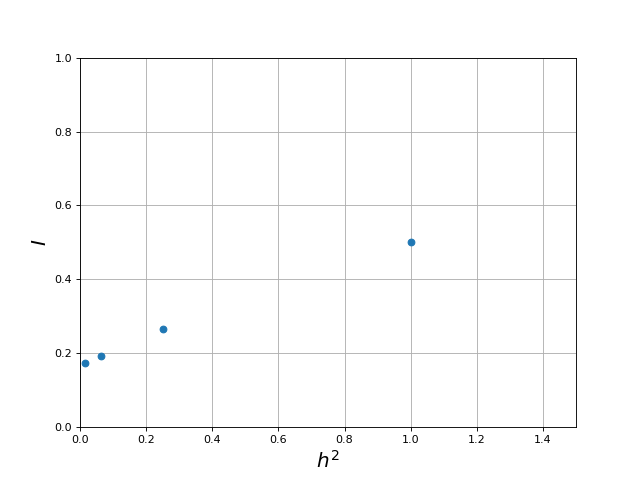figB.pdf

L'estimation la plus précise de l'intégrale est I₃, obtenue pour N=2³=8. Son erreur peut être lue sur le graphique tracé plus haut. On pourrait obtenir une estimation ayant une erreur plus faible avec p=4, ce qui nécessiterait le calcul d'une somme de 2³ termes, avec autant d'évaluations de la fonction f. La méthode de Romberg consiste à utiliser les valeurs déjà calculées I₀,I₁,I₂,I₃ pour obtenir une meilleure estimation de l'intégrale, sans avoir à faire de nouvelles évaluations de la fonction f. Elle repose sur le fait que l'erreur s'exprime en fonction de h². Une estimation de l'intégrale beaucoup plus précise est donc obtenue en extrapolant les points (h_p²,I_p) déjà calculés jusqu'à h²=0.

La méthode de Romberg est une méthode d'accélération de convergence par extrapolation, appelée aussi extrapolation de Richardson.

3.b. Extrapolation polynomiale

Une extrapolation polynomiale est effectuée en cherchant le polynôme de Lagrange passant par les points (h_p²,I_p). Ce polynôme est évalué en h²=0. On utilise pour cela l'algorithme de Neville.

L'algorithme de Neville est développé de manière itérative (et non pas récursive). Les différents termes à calculer sont placés dans une matrice que l'on génère ligne après ligne :

$$\begin{array}{cccc}\hfill A_{0,0}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill A_{1,0}\hfill & \hfill A_{1,1}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill A_{2,0}\hfill & \hfill A_{2,1}\hfill & \hfill A_{2,2}\hfill & \hfill \hfill \\ \hfill A_{3,0}\hfill & \hfill A_{3,1}\hfill & \hfill A_{3,2}\hfill & \hfill A_{3,3}\hfill \end{array}\text{(7)}$$

Le premier terme correspond à la première estimation de l'intégrale A_0,0=I₀. Le premier élément de la deuxième ligne est la seconde estimation de l'intégrale A_1,0=I₁. À partir des deux points (h₀²,A_0,0) et (h₁²,A_1,0), on effectue une extrapolation en h²=0 par un polynôme de degré 1. Le résultat de cette extrapolation est donnée par la relation de récurrence de Neville :

$$A_{1,1}=\frac{-h_1^2{A}_{0,0}+h_0^2{A}_{1,0}}{h_0^2-h_1^2}=A_{1,0}+\frac{A_{10}-A_{0,0}}{(\frac{h_0}{h_1}{)}^2-1}\text{(8)}$$

La seconde écriture fait apparaître le terme correctif par rapport à la dernière estimation de l'intégrale. Si ce terme correctif est inférieur à une tolérance ε alors on arrête l'itération. Dans le cas contraire, on calcule A_2,0=I₂ puis on effectue une extrapolation polynomiale de degré 2. Celle-ci se fait en calculant tout d'abord A_2,1, l'extrapolation de degré 1 obtenue avec A_1,0 et A_2,0, puis en calculant A_2,2, l'extrapolation de degré 2 calculée à partir de A_1,1 et A_2,1.

L'application de la formule de récurrence de Neville conduit à :

$$A_{j,i}=A_{j,i-1}+\frac{A_{j,i-1}-A_{j-1,i-1}}{(\frac{h_{j-i}}{h_j}{)}^2-1}\text{pour}i=1,1,\dots ,j\text{(9)}$$

Cette formule permet de calculer la ligne j. Le premier élément de cette ligne est A_j,0=I_j. Le dernier élément A_j,j est l'extrapolation de degré j. Si le terme correctif par rapport à A_j,j-1 a une valeur absolue inférieure à la tolérance alors A_j,j est l'estimation finale de l'intégrale. Dans le cas contraire, on effectue le calcul de la ligne suivante pour faire une extrapolation de degré j+1.

En explicitant h_i, la formule de récurence s'écrit :

$$A_{j,i}=A_{j,i-1}+\frac{A_{j,i-1}-A_{j-1,i-1}}{4^i-1}\text{pour}i=1,2,\dots ,j\text{(10)}$$

3.c. Implémentation et exemples

Une fonction romberg(epsilon) est ajoutée à la classe Romberg. La fonction renvoie la matrice A et la meilleure estimation de l'intégrale.

On reprend l'exemple précédent :

def f(x):
    return x**5
romberg = Romberg(f,0,1)
(h,I) = romberg.trapezes(1e-7)
                    

print(I[-1]-1.0/6)
--> 2.4835268314093994e-08

print(romberg.n_eval)
--> 4095

romberg = Romberg(f,0,1)
(A,I) = romberg.romberg(1e-7)
                    

print(I-1.0/6)
--> 0.0

print(romberg.n_eval)
--> 7

Avec la méthode des Trapèzes itérative, 4095 évaluations de la fonction sont nécessaires pour arriver à une erreur de l'ordre de 10^-8. Avec la méthode de Romberg, seulement 7 évaluations sont nécessaires pour arriver à une erreur inférieure à la précision des nombres flottants (il s'agit bien sûr d'un cas très favorable). Voici la matrice A, qui permet de voir les extrapolations effectuées :

print(A)
--> array([[0.5       , 0.        , 0.        ],
       [0.265625  , 0.1875    , 0.        ],
       [0.19238281, 0.16796875, 0.16666667]])

Le premier élément de la troisième ligne est obtenu avec la formule des trapèzes pour N=4. L'extrapolation à 3 points, par un polynôme de degré 2, permet d'obtenir la valeur exacte (à la précision des flottants près). Sur cet exemple, l'expression de I_p en fonction de h² est probablement un polynome de degré 2.

Voyons un autre exemple plus intéressant, où l'on ne connaît pas d'expression analytique de la primitive :

$$erf\left(z\right)=\frac{2}{\sqrt{\pi }}{\int }_0^{z}exp(-x^2)dx\text{(11)}$$

La fonction scipy.special.erf(z) fournit sa valeur. On fait le test pour z=1.

from scipy.special import erf
def f(x):
    return numpy.exp(-x*x)
romberg = Romberg(f,0,1)
(h,I) = romberg.trapezes(1e-7)
                    

print(I[-1]-numpy.sqrt(numpy.pi)/2*erf(1))
--> -1.4618215860018324e-08

print(romberg.n_eval)
--> 2047

romberg = Romberg(f,0,1)
(A,I) = romberg.romberg(1e-7)
                    

print(I-numpy.sqrt(numpy.pi)/2*erf(1))
--> 2.826674450062683e-10

print(romberg.n_eval)
--> 15

La méthode de Romberg nécessite seulement 15 évaluations de la fonction (et l'erreur est plus faible), contre 2047 pour la méthode des trapèzes itérative.

print(A)
--> array([[0.68393972, 0.        , 0.        , 0.        ],
       [0.73137025, 0.74718043, 0.        , 0.        ],
       [0.7429841 , 0.74685538, 0.74683371, 0.        ],
       [0.74586561, 0.74682612, 0.74682417, 0.74682402]])

Le résultat est obtenu avec une extrapolation par un polynôme de degré 3.

Considérons l'intégrale suivante :

$${\int }_0^1\sqrt{1-x^2}dx=\frac{\pi }{4}\text{(12)}$$

from scipy.special import erf
def f(x):
    return numpy.sqrt(1-x*x)
romberg = Romberg(f,0,1)
(h,I) = romberg.trapezes(1e-7)
                    

print(I[-1]-numpy.pi/4)
--> -4.9563892989823444e-08

print(romberg.n_eval)
--> 32767

romberg = Romberg(f,0,1)
(A,I) = romberg.romberg(1e-7)
                    

print(I-numpy.pi/4)
--> -0.00018949376813126584

print(romberg.n_eval)
--> 63

Pour cette intégrale, l'erreur finale obtenue avec la méthode de Romberg est beaucoup plus grande que la tolérance demandée, ce qui signifie que l'extrapolation ne fonctionne pas bien. On peut essayer de réduire la tolérance :

romberg = Romberg(f,0,1)
(A,I) = romberg.romberg(1e-15)
                    

print(I-numpy.pi/4)
--> -4.623325045027826e-08

print(romberg.n_eval)
--> 16383

On arrive à la même erreur que la méthode des trapèzes, mais le nombre d'évaluations n'est que deux fois moindre. Pour cette fonction, la méthode de Romberg est donc peu efficace.

En principe, la méthode de Romberg fonctionne avec une grande efficacité lorsque la fonction à intégrer est infiniment dérivable sur l'intervalle d'intégration. Ce n'est pas le cas du dernier exemple, dont la dérivée n'est pas définie en x=1.